10 câu hỏi trắc nghiệm thuộc Dạng 5. Phương trình đoạn chắn của đường thẳng

Câu 1:

Trong mặt phẳng tọa độ Oxy, phương trình đường thẳng cắt hai trục tọa độ tại hai điểm M(–1; 0) và N(0; 2) là

A. 2x – y + 2 = 0;

B. 2x + y – 2 = 0;

C. 2x + y + 2 = 0;

D. 2x – y + 1 = 0.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A

Đường thẳng MN cắt hai trục tọa độ tại hai điểm M(–1; 0) và N(0; 2) nên phương trình đường thẳng MN theo đoạn chắn là: $\frac{x}{- 1} + \frac{y}{2} = 1$ , tức là 2x – y + 2 = 0.

Câu 2:

Trong mặt phẳng tọa độ Oxy, phương trình đường thẳng đi qua hai điểm A(0; –3) và B(4; 0) là

A.

\frac{x}{- 3} + \frac{y}{4} = 1

;

B. $\frac{x}{4} + \frac{y}{- 3} = 1$ ;

C. $\frac{x}{4} + \frac{y}{3} = 1$ ;

D.

\frac{x}{4} + \frac{y}{3} = - 1

.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B

Đường thẳng AB đi qua hai điểm A(0; –3) và B(4; 0) có phương trình là: $\frac{x}{4} + \frac{y}{- 3} = 1$ .

Câu 3:

Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: 2x – y + 4 = 0. Phương trình đoạn chắn của đường thẳng d là

A. $\frac{x}{- 2} + \frac{y}{4} = 1$ ;

B. $\frac{x}{2} + \frac{y}{- 4} = 1$ ;

C. $\frac{x}{- 2} + \frac{y}{- 4} = 1$ ;

D.

\frac{x}{4} + \frac{y}{2} = 1

.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A

Xét đường thẳng d: 2x – y + 4 = 0.

Giao với trục Oy: Cho x = 0 ta có y = 4;

Giao với trục Ox: Cho y = 0 ta có x = –2.

Đường thẳng d cắt trục Ox tại A(–2; 0) và cắt trục Oy tại B(0; 4) có phương trình đoạn chắn là: $\frac{x}{- 2} + \frac{y}{4} = 1.$

Câu 4:

Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: $\{\begin{cases} x = 4 + t \\ y = 3 - 2 t \end{cases} .$ Phương trình đoạn chắn của đường thẳng d là:

A. $\frac{x}{11} + \frac{y}{22} = \frac{1}{2};$

B. $\frac{x}{\frac{11}{2}} + \frac{y}{11} = 1;$

C. $\frac{x}{11} + \frac{y}{\frac{11}{2}} = 1;$

D. $\frac{x}{22} + \frac{y}{11} = \frac{1}{2} .$

Xem đáp án

Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: x = 4 + t và y= 3- 2t Phương trình đoạn chắn của đường thẳng d là: (ảnh 1)

Câu 5:

Trong mặt phẳng tọa độ Oxy, cho điểm M(1; 2). Gọi A, B là hình chiếu của M lên Ox, Oy. Phương trình đường thẳng AB theo đoạn chắn là

A. 2x + y – 2 = 0;

B. $\frac{x}{1} + \frac{y}{2} = 1;$

C. x + 2y – 2 = 0;

D.

\frac{x}{2} + \frac{y}{1} = 1;

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B

Ta có hình chiếu của điểm M(1; 2) lên Ox, Oy lần lượt là A(1; 0) và B(0; 2).

Do đó phương trình đường thẳng AB theo đoạn chắn là $\frac{x}{1} + \frac{y}{2} = 1.$

Câu 6:

Trong mặt phẳng tọa độ Oxy, phương trình đường thẳng đi qua điểm Q(–1; –1) và cắt hai trục tọa độ tại hai điểm A và B sao cho tam giác OAB vuông cân là:

A. x + y – 2 = 0;

B. x – y – 2 = 0;

C. x – y + 2 = 0;

D. x + y + 2 = 0.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D

Gọi điểm A thuộc vào trục Ox, điểm B thuộc vào trục Oy. Khi đó: A(a; 0) và B(0; b).

Phương trình đoạn chắn của đường thẳng AB là: $\frac{x}{a} + \frac{y}{b} = 1$ .

Do tam giác OAB vuông cân tại O nên suy ra |a| = |b|. Xảy ra 2 trường hợp như sau:

⦁ Trường hợp 1.

Với b = a ta có phương trình đoạn chắn của đường thẳng AB là: $\frac{x}{a} + \frac{y}{b} = 1$ , tức là x + y – a = 0.

Mà Q(–1; –1) thuộc vào đường thẳng AB nên ta có: –1 – 1 – a = 0, suy ra a = –2 và b = –2.

Vậy phương trình đường thẳng AB là: x + y + 2 = 0.

⦁ Trường hợp 2.

Với b = –a ta có phương trình đoạn chắn của đường thẳng AB là: $\frac{x}{a} + \frac{y}{- a} = 1 \Leftrightarrow x - y = a$ .

Mà Q(–1; –1) thuộc vào đường thẳng AB nên ta có: –1 + 1 – a = 0, suy ra a = 0 và b = 0 (loại vì khi đó ba điểm A, B, O trùng nhau).

Vậy phương trình đường thẳng AB là: x + y + 2 = 0.

Câu 7:

Trong mặt phẳng tọa độ Oxy, cho đường thẳng d đi qua M(–2; 7) và cắt hai trục tọa độ tại hai điểm A và B sao cho M là trung điểm của AB. Phương trình đường thẳng d theo đoạn chắn là

A. $\frac{x}{4} - \frac{y}{14} = - 1;$

B. $\frac{x}{14} - \frac{y}{4} = - 1;$

C. $\frac{x}{- 4} + \frac{y}{14} = 1;$

D.

\frac{x}{14} + \frac{y}{- 4} = 1.

Xem đáp án

Đáp án đúng là: C

Gọi A là điểm thuộc trục Ox, B là điểm thuộc trục Oy. Khi đó A(x_A; 0) và B(0; y_B).

Ta có M là trung điểm của AB suy ra: $\{\begin{cases} x_{A} + x_{B} = 2 x_{M} \\ y_{A} + y_{B} = 2 y_{M} \end{cases} \Leftrightarrow \{\begin{cases} x_{A} = - 4 \\ y_{B} = 14 \end{cases}$ .

Do đó A(–4; 0) và B(0; 14).

Khi đó phương trình đoạn chắn của đường thẳng d là: $\frac{x}{- 4} + \frac{y}{14} = 1.$

Câu 8:

Trong mặt phẳng tọa độ Oxy, cho đường thẳng d cắt hai trục tọa độ Ox, Oy lần lượt tại hai điểm A và B. Biết điểm M(–4; 6) và B là trung điểm của AM. Phương trình đường thẳng d theo đoạn chắn là

A. $\frac{x}{3} - \frac{y}{4} = 1;$

B. $\frac{x}{3} + \frac{y}{4} = 1;$

C. $\frac{x}{4} - \frac{y}{3} = 1;$

D.

\frac{x}{4} + \frac{y}{3} = 1;

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

Đường thẳng d cắt hai trục tọa độ Ox, Oy lần lượt tại hai điểm A và B nên ta gọi A(x_A; 0) và B(0; y_B).

Vì B là trung điểm của AM với M(–4; 6) nên ta có

$\{\begin{cases} x_{B} = \frac{x_{A} + x_{M}}{2} \\ y_{B} = \frac{y_{A} + y_{M}}{2} \end{cases} \Leftrightarrow \{\begin{cases} 0 = \frac{x_{A} - 4}{2} \\ y_{B} = \frac{0 + 6}{2} \end{cases} \Leftrightarrow \{\begin{cases} x_{A} = 4 \\ y_{B} = 3 \end{cases} .$ Do đó A(4; 0) và B(0; 3).

Khi đó phương trình đoạn chắn của đường thẳng d là: $\frac{x}{4} + \frac{y}{3} = 1.$

Câu 9:

Trong mặt phẳng tọa độ Oxy, cho điểm M(1; 2). Đường thẳng d đi qua M (không đi qua gốc O) và chắn hai trục tọa độ hai đoạn thẳng có độ dài bằng nhau. Phương trình nào sau đây là một phương trình đoạn chắn của đường thẳng d?

A. $\frac{x}{1} + \frac{y}{1} = 1;$

B. $\frac{x}{3} + \frac{y}{3} = 1;$

C. $\frac{x}{3} - \frac{y}{3} = 1;$

D.

\frac{x}{1} + \frac{y}{3} = 1.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: B

Giả sử đường thẳng d có phương trình đoạn chắn $\frac{x}{a} + \frac{y}{b} = 1$ (với a, b ≠ 0).

Vì đường thẳng d chắn hai trục tọa độ hai đoạn thẳng có độ dài bằng nhau nên |a| = |b|.

⦁ Trường hợp 1. Nếu b = a thì ta có $\frac{x}{a} + \frac{y}{b} = 1$

Vì M(1; 2) ∈ d nên $d : \frac{1}{a} + \frac{2}{a} = 1 \Leftrightarrow \frac{3}{a} = 1 \Leftrightarrow a = 3.$ Suy ra b = 3.

Khi đó ta có $d : \frac{x}{3} + \frac{y}{3} = 1.$

⦁ Trường hợp 2. Nếu b = –a thì ta có $d : \frac{x}{a} + \frac{y}{- a} = 1$

Vì M(1; 2) ∈ d nên $d : \frac{1}{a} + \frac{2}{- a} = 1 \Leftrightarrow \frac{- 1}{a} = 1 \Leftrightarrow a = - 1.$ Suy ra b = 1.

Khi đó ta có $d : \frac{x}{- 1} + \frac{y}{1} = 1.$

Trong các phương án, ta thấy phương án B là đúng.

Câu 10:

Trong mặt phẳng tọa độ Oxy, cho đường thẳng d đi qua điểm M(3; 2), cắt tia Ox tại A và cắt tia Oy tại B sao cho diện tích tam giác OAB đạt giá trị nhỏ nhất. Khi đó phương trình đường thẳng d theo đoạn chắn là:

A. $\frac{x}{4} + \frac{y}{6} = 1;$

B. $\frac{x}{6} + \frac{y}{4} = 1;$

C. $\frac{x}{\frac{3}{2}} + \frac{y}{1} = 1;$

D.

\frac{x}{1} + \frac{y}{\frac{3}{2}} = 1.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: B

Gọi A(a; 0) và B(0; b) (với a > 0, b > 0).

Khi đó phương trình đoạn chắn của d có dạng: $\frac{x}{a} + \frac{y}{b} = 1.$

Đường thẳng d đi qua điểm M(3; 2) nên ta có $\frac{3}{a} + \frac{2}{b} = 1.$

Ta có diện tích tam giác OAB là: $S = \frac{1}{2} O A \cdot O B = \frac{1}{2} |a| \cdot |b| = \frac{1}{2} a b .$

Áp dụng BĐT Cauchy, ta được

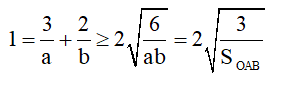
Trong mặt phẳng tọa độ Oxy, cho đường thẳng d đi qua điểm M(3; 2), cắt tia Ox tại A và cắt tia Oy tại (ảnh 1)

Suy ra S_OAB ≥ 12.

Dấu “=” xảy ra khi và chỉ khi $\frac{3}{a} = \frac{2}{b} = \frac{1}{2} \Leftrightarrow \{\begin{cases} a = 6 \\ b = 4 \end{cases} .$

Vậy đường thẳng d có phương trình theo đoạn chắn là $\frac{x}{6} + \frac{y}{4} = 1.$

Trắc nghiệm Toán 10 Bài 19. Phương trình đường thẳng có đáp án

Dạng 5. Phương trình đoạn chắn của đường thẳng

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương