10 câu hỏi trắc nghiệm thuộc Dạng 4. Viết phương trình cạnh, đường cao, trung tuyến, phân giác của tam giác

Câu 1:

Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(1; 2), B(3; 1), C(5; 4). Phương trình nào sau đây là phương trình đường cao kẻ từ A của tam giác ABC?

A. 2x + 3y – 8 = 0;

B. 2x – 3y + 8 = 0;

C. 3x – 2y + 1 = 0;

D. 2x + 3y – 2 = 0.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A

Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(1; 2), B(3; 1), C(5; 4). Phương trình nào sau đây (ảnh 1)

Với B(3; 1) và C(5; 4), ta có .

Đường cao kẻ từ A của tam giác ABC nhận làm vectơ pháp tuyến và đi qua điểm A(1; 2) nên có phương trình là: 2(x – 1) + 3(y – 2) = 0 tức là 2x + 3y – 8 = 0.

Vậy phương trình đường cao kẻ từ A của tam giác ABC là: 2x + 3y – 8 = 0.

Câu 2:

Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(0; –2), B(1; 1), C(4; 2). Phương trình đường trung tuyến của tam giác ABC kẻ từ A là

A. 7x + 7y + 14 = 0;

B. 5x – 3y + 1 = 0;

C. 3x + y – 2 = 0;

D. –7x + 5y + 10 = 0.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D

Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(0; –2), B(1; 1), C(4; 2). Phương trình đường trung tuyến của tam giác ABC kẻ từ A là (ảnh 1)

Gọi M là trung điểm của cạnh BC .

Với B(1; 1) và C(4; 2), ta có $M (\frac{5}{2}; \frac{3}{2}),$ .

Với A(0; –2) và $M (\frac{5}{2}; \frac{3}{2})$ ta có $\vec{A M} = (\frac{5}{2}; \frac{7}{2})$ .

Đường trung tuyến AM nhận $\vec{A M} = (\frac{5}{2}; \frac{7}{2})$ làm một vectơ chỉ phương nên nhận $\vec{n} = (- 7; 5)$ làm một vectơ pháp tuyến.

Vậy phương trình đường trung tuyến kẻ từ A của tam giác ABC là:

–7x + 5(y + 2) = 0 hay –7x + 5y + 10 = 0.

Câu 3:

Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(–2; –1), B(–1; 3), C(6; 1). Phương trình đường phân giác trong góc A của tam giác ABC là

A. x – y + 1 = 0;

B. 5x + 3y + 9 = 0;

C. 3x + 3y – 5 = 0;

D. x + y + 3 = 0.

Xem đáp án

Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(–2; –1), B(–1; 3), C(6; 1). Phương trình đường phân (ảnh 1)

Câu 4:

Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(–2; –1), B(–1; 3), C(6; 1). Phương trình đường phân giác ngoài góc A của tam giác ABC là

A. x – y + 1 = 0;

B. 5x + 3y + 9 = 0;

C. 3x + 3y – 5 = 0;

D. x + y + 3 = 0.

Xem đáp án

Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(–2; –1), B(–1; 3), C(6; 1). Phương trình đường phân giác ngoài góc A của tam giác ABC là (ảnh 1)

Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(–2; –1), B(–1; 3), C(6; 1). Phương trình đường phân giác ngoài góc A của tam giác ABC là (ảnh 2)

Câu 5:

Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(2; −1) và hai đường cao xuất phát từ B và C có phương trình lần lượt là: 2x – y + 1 = 0 và 3x + y + 2 = 0. Phương trình cạnh BC là

A. 9x – 2y + 10 = 0;

B. 9x – 2y – 10 = 0;

C. 2x + 9y + 9 = 0;

D. 9x – 2y – 2 = 0.

Xem đáp án

Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(2; −1) và hai đường cao xuất phát từ B và C có phương trình lần lượt (ảnh 2)

Câu 6:

Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(1; 3) và hai đường trung tuyến BM: x – 2y + 1 = 0 và CN: y – 1 = 0. Phương trình đường thẳng AB là

A. $\{\begin{cases} x = 1 + t \\ y = 3 - t \end{cases}$ ;

B. $\{\begin{cases} x = 1 + t \\ y = 3 + t \end{cases}$ ;

C. $\{\begin{cases} x = 1 - t \\ y = 3 + t \end{cases}$ ;

D.

\{\begin{cases} x = 1 - t \\ y = 3 - t \end{cases}

.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B

Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(1; 3) và hai đường trung tuyến BM: (ảnh 1)

Tọa độ trọng tâm G của tam giác ABC là giao điểm của BM và CN nên là nghiệm của hệ phương trình:

$\{\begin{cases} x - 2 y + 1 = 0 \\ y - 1 = 0 \end{cases} \Leftrightarrow \{\begin{cases} x = 1 \\ y = 1 \end{cases} .$ Do đó G (1; 1).

Gọi B(x_B; y_B). Vì điểm B thuộc đường trung tuyến BM: x – 2y + 1 = 0 nên ta có:

x_B – 2y_B + 1 = 0, suy ra x_B = 2y_B – 1. Khi đó B(2y_B – 1; y_B).

Gọi C(x_C; y_C). Vì điểm C thuộc đường trung tuyến CN: y – 1 = 0 nên ta có:

y_C – 1 = 0, suy ra y_C = 1. Khi đó C(x_C; 1).

Vì G là trọng tâm của tam giác ABC nên ta có:

$\{\begin{cases} x_{G} = \frac{x_{A} + x_{B} + x_{C}}{3} \\ y_{G} = \frac{y_{A} + y_{B} + y_{C}}{3} \end{cases} \Leftrightarrow \{\begin{cases} 1 = \frac{1 + 2 y_{B} - 1 + x_{C}}{3} \\ 1 = \frac{3 + y_{B} + 1}{3} \end{cases} \Leftrightarrow \{\begin{cases} 2 y_{B} + x_{C} = 3 \\ y_{B} + 4 = 3 \end{cases} \Leftrightarrow \{\begin{cases} x_{C} = 5 \\ y_{B} = - 1 \end{cases}$ .

Từ đó ta có tọa độ hai điểm B và C là: B(–3; –1) và C(5; 1).

Với A(1; 3) và B(–3; –1), ta có $\vec{A B} = (- 4; - 4)$

Phương trình đường thẳng AB đi qua A(1; 3) và có vectơ chỉ phương $\vec{u} = (1; 1)$ là:

$\{\begin{cases} x = 1 + t \\ y = 3 + t \end{cases}$ .

Câu 7:

Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có tọa độ trung điểm các cạnh BC, AC, AB lần lượt là M(2; 1), N(5; 3), P(3; –4). Phương trình đường thẳng BC là

A. 5x + y – 28 = 0;

B. 7x + 2y – 12 = 0;

C. 7x – 2y – 12 = 0;

D. 2x – 3y – 18 = 0.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C

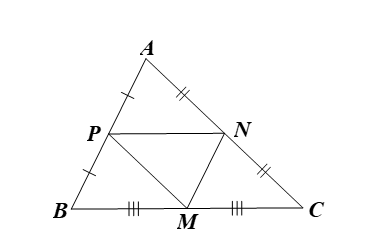
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có tọa độ trung điểm các cạnh BC, AC, AB lần (ảnh 1)

Với N(5; 3) và P(3; –4), ta có: $\vec{N P} = (- 2; - 7)$ .

Xét ∆ABC có N, P lần lượt là trung điểm của AC, AB nên NP là đường trung bình của tam giác. Do đó NP // BC.

Khi đó đường thẳng BC nhận $\vec{N P} = (- 2; - 7)$ làm một vectơ chỉ phương nên có một vectơ pháp tuyến là $\vec{n} = (7; - 2) .$

Đường thẳng BC đi qua M(2; 1) và có vectơ pháp tuyến $\vec{n} = (7; - 2) .$ nên có phương trình là:

7(x – 2) – 2(y – 1) = 0 tức là 7x – 2y – 12 = 0.

Đường thẳng AC song song với đường thẳng MP nên phương trình đường thẳng AC đi qua N và có vectơ pháp tuyến $\vec{n_{2}} = (5; 1)$ là:

5(x – 5) + 1(y – 3) = 0 tức là 5x + y – 28 = 0.

Đường thẳng BC song song với đường thẳng MN nên phương trình đường thẳng BC đi qua P và có vectơ pháp tuyến $\vec{n_{3}} = (2; - 3)$ là:

2(x – 3) – 3(y + 4) = 0 tức là 2x – 3y – 18 = 0.

Câu 8:

Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có M(2; 0) là trung điểm của cạnh AB. Đường trung tuyến và đường cao từ đỉnh A có phương trình lần lượt là: 7x – 2y – 3 = 0 và 6x – y – 4 = 0. Phương trình đường thẳng AC là

A. 3x – 4y – 5 = 0;

B. 3x + 4y + 5 = 0;

C. 3x – 4y + 5 = 0;

D. 3x + 4y – 5 = 0;

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C

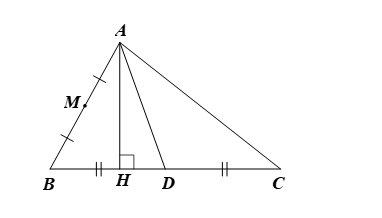
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có M(2; 0) là trung điểm của cạnh AB. Đường trung tuyến và đường (ảnh 1)

⦁ Gọi AH và AD lần lượt là các đường cao và trung tuyến kẻ từ A của tam giác ABC.

Tọa độ điểm A là nghiệm của hệ phương trình:

$\{\begin{cases} 7 x - 2 y - 3 = 0 \\ 6 x - y - 4 = 0 \end{cases} \Leftrightarrow \{\begin{cases} x = 1 \\ y = 2 \end{cases} .$ Do đó A(1; 2).

Vì M là trung điểm của AB nên: $\{\begin{cases} x_{B} = 2 x_{M} - x_{A} = 3 \\ y_{B} = 2 y_{M} - y_{A} = - 2 \end{cases} .$ Do đó B(3; –2).

⦁ Ta có AH ⊥ BC nên vectơ chỉ phương của AH là vectơ pháp tuyến của BC.

Đường thẳng AH: 6x – y – 4 = 0 có ${\vec{n}}_{A H} = (6; - 1)$ nên ${\vec{n}}_{B C} = (1; 6) .$

Đường thẳng BC đi qua B(3; –2) và nhận ${\vec{n}}_{B C} = (1; 6)$ làm một vectơ pháp tuyến nên có phương trình là: 1(x – 3) + 6(y + 2) = 0 hay x + 6y + 9 = 0.

⦁ D là giao điểm của BC và AD nên tọa độ điểm D là nghiệm của hệ phương trình:

$\{\begin{cases} 7 x - 2 y - 3 = 0 \\ x + 6 y + 9 = 0 \end{cases} \Leftrightarrow \{\begin{cases} x = 0 \\ y = - \frac{3}{2} \end{cases} .$ Do đó $D (0; - \frac{3}{2}) .$

Mà D là trung điểm của BC nên suy ra: $\{\begin{cases} x_{C} = 2 x_{D} - x_{B} = - 3 \\ y_{C} = 2 y_{D} - y_{B} = - 1 \end{cases} .$ Do đó C(–3; –1).

⦁ Với A(1; 2) và C(–3; –1) ta có $\vec{A C} = (- 4; - 3),$ suy ra ${\vec{n}}_{A C} = (3; - 4) .$

Đường thẳng AC đi qua A(1; 2) và nhận ${\vec{n}}_{A C} = (3; - 4)$ làm một vectơ pháp tuyến nên có phương trình là: 3(x – 1) – 4(y – 2) = 0 tức là 3x – 4y + 5 = 0.

Câu 9:

Trong mặt phẳng cho tam giác ABC cân tại C có B(2; –1), A(4; 3). Phương trình đường cao CH là

A. x – 2y – 1 = 0;

B. x – 2y + 1 = 0;

C. 2x + y – 2 = 0;

D. x + 2y – 5 = 0.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D

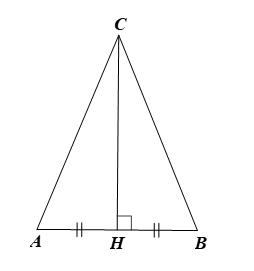
Trong mặt phẳng cho tam giác ABC cân tại C có B(2; –1), A(4; 3). Phương trình đường cao CH (ảnh 1)

Gọi H là trung điểm của AB.

Tam giác ABC cân tại C nên đường trung tuyến CH đồng thời là đường cao, do đó CH ⊥ AB.

Khi đó đường cao CH nhận vectơ chỉ phương của AB làm một vectơ pháp tuyến.

Với B(2; –1) và A(4; 3), ta có H(3; 1) và $\vec{A B} = (- 2; - 4) = - 2 (1; 2) .$

Khi đó đường cao CH đi qua điểm H(3; 1) và nhận $\vec{n} = (1; 2)$ làm một vectơ pháp tuyến nên có phương trình là: 1(x – 3) + 2(y – 1) = 0, tức là x + 2y – 5 = 0.

Câu 10:

Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có A(2; 4), B(5; 0) và C(2; 1). Trung tuyến BM của tam giác đi qua điểm N có hoành độ bằng 20 thì tung độ bằng

A. –12;

B. $- \frac{25}{2};$

C. –13;

D.

- \frac{27}{2} .

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B

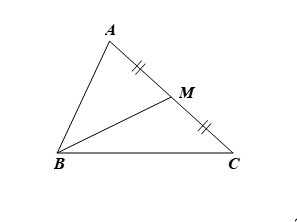
Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có A(2; 4), B(5; 0) và C(2; 1). Trung tuyến BM (ảnh 1)

Với A(2; 4) và C(2; 1) ta có tọa độ trung điểm M của AC là $M (2; \frac{5}{2}) .$

Với B(5; 0) và $M (2; \frac{5}{2}) .$ ta có $\vec{M B} = (3; - \frac{5}{2}) = \frac{1}{2} (6; - 5) .$

Đường thẳng BM đi qua B(5; 0) và nhận $\vec{u} = (6; - 5)$ làm một vectơ chỉ phương nên có phương trình tham số là: $\{\begin{cases} x = 5 + 6 t \\ y = - 5 t \end{cases} .$

Điểm N(20; y_N) nằm trên đường thẳng BM nên ta có $\{\begin{cases} 20 = 5 + 6 t \\ y_{N} = - 5 t \end{cases} \Leftrightarrow \{\begin{cases} t = \frac{5}{2} \\ y_{N} = - \frac{25}{2} \end{cases} .$

Vậy ta chọn phương án B.

Trắc nghiệm Toán 10 Bài 19. Phương trình đường thẳng có đáp án

Dạng 4. Viết phương trình cạnh, đường cao, trung tuyến, phân giác của tam giác

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương