Câu hỏi:
03/04/2024 31
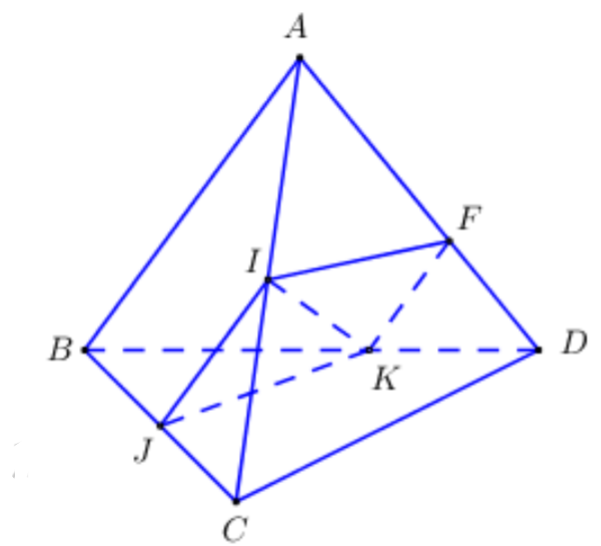
Cho tứ diện ABCD. Gọi I, J lần lượt là trung điểm của AC và BC. Trên cạnh BD lấy điểm K sao cho BK = 2KD. Gọi F là giao điểm của AD với mặt phẳng (IJK). Tính tỉ số\[\frac{{FA}}{{FD}}.\]
A. \[\frac{7}{3}\]
B. 2
C. \[\frac{{11}}{5}\]
D. \[\frac{5}{3}\]
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án B
Phương pháp:
+ Dựng giao tuyến dựa vào các yếu tố song song.
+ Sử dụng định lí Ta-lét.
Cách giải:
\[\left\{ \begin{array}{l}\left( {IJK} \right) \supset IJ\\\left( {ABD} \right) \supset AB\\IJ\parallel AB\\K \in \left( {IJK} \right) \cap \left( {ABD} \right)\end{array} \right. \Rightarrow \]Giao tuyến của hai mặt phẳng \[\left( {IJK} \right)\]và \[\left( {ABD} \right)\]là đường thẳng đi qua K và song song với IJ, AB.
Trong \[\left( {ABD} \right)\]kẻ\[KF\parallel AB\left( {F \in AD} \right)\], khi đó ta có\[\left( {IJK} \right) \cap \left( {ABD} \right) = KF \Rightarrow \left( {IJK} \right) \cap AD = F\]
Áp dụng định lí Ta-lét ta có\[\frac{{FA}}{{FD}} = \frac{{KB}}{{KD}} = 2.\]
Đáp án B
Phương pháp:
+ Dựng giao tuyến dựa vào các yếu tố song song.
+ Sử dụng định lí Ta-lét.

Cách giải:
\[\left\{ \begin{array}{l}\left( {IJK} \right) \supset IJ\\\left( {ABD} \right) \supset AB\\IJ\parallel AB\\K \in \left( {IJK} \right) \cap \left( {ABD} \right)\end{array} \right. \Rightarrow \]Giao tuyến của hai mặt phẳng \[\left( {IJK} \right)\]và \[\left( {ABD} \right)\]là đường thẳng đi qua K và song song với IJ, AB.
Trong \[\left( {ABD} \right)\]kẻ\[KF\parallel AB\left( {F \in AD} \right)\], khi đó ta có\[\left( {IJK} \right) \cap \left( {ABD} \right) = KF \Rightarrow \left( {IJK} \right) \cap AD = F\]
Áp dụng định lí Ta-lét ta có\[\frac{{FA}}{{FD}} = \frac{{KB}}{{KD}} = 2.\]
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hai đường thẳng song song. Trên đường thẳng thứ nhất ta lấy 20 điểm phân biệt. Trên đường thẳng thứ hai ta lấy 18 điểm phân biệt. Hỏi có bao nhiêu tam giác được tạo thành từ 3 điểm trong các điểm nói trên?
Câu 2:
Biết hệ số của số hạng chứa\[{x^2}\]trong khai triển\[{\left( {1 + 4x} \right)^n}\]là 3040. Số tự nhiên n bằng bao nhiêu?
Câu 3:
b) Một hộp đựng tám thẻ được ghi từ 1 đến 8. Lấy ngẫu nhiên từ hộp đó ba thẻ, tính xác suất để tổng các số ghi trên ba thẻ đó bằng 11.
Câu 4:
Tìm tập xác định của hàm số\[y = \sqrt {\frac{{1 + \cos x}}{{1 - \sin x}}} .\]
Câu 5:
Tìm số hạng không chứa x trong khai triển\[{\left( {{x^3} - \frac{1}{x}} \right)^{12}}.\]
Câu 6:
Có bao nhiêu số nguyên m để phương trình \(12\sin x - 5\cos x = m\)có nghiệm.
Câu 7:
Trong mặt phẳng tọa độ Oxy cho đường tròn\[\left( C \right):{\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = 4\]. Phép đối xứng trục Ox biến đường tròn (C) thành đường tròn\[\left( {C'} \right)\]có phương trình là:
Câu 8:
Cho hình chóp S.ABCD, biết AC cắt BD tại M, AB cắt CD tại O. Tìm giao tuyến của hai mặt phẳng (SAB) và (SCD) .
Câu 9:
Hàm số nào sau đây đồng biến trên khoảng\[\left( {\frac{\pi }{2};\pi } \right)\]?
Câu 10:
Một bộ đề thi Olimpic Toán lớp 11 của Trường THPT Kim Liên mà mỗi đề gồm 5 câu được chọn từ 15 câu mức dễ, 10 câu mức trung bình và 5 câu mức khó. Một đề thi được gọi là “Tốt” nếu trong đề thi phải có cả mức dễ, trung bình và khó, đồng thời số câu mức khó không ít hơn 2. Lấy ngẫu nhiên một đề thi trong bộ đề trên. Tìm xác suất để đề thi lấy ra là một đề thi “Tốt”.
Câu 11:
Một người vào cửa hàng ăn, người đó chọn thực đơn gồm 1 món ăn trong 5 món khác nhau, 1 loại quả tráng miệng trong 5 loại quả tráng miệng khác nhau và một loại đồ uống trong 3 loại đồ uống khác nhau. Có bao nhiêu cách chọn thực đơn?
Câu 12:
Gieo con súc sắc cân đối đồng chất 2 lần. Tính xác suất để tích số chấm xuất hiện ở hai lần là một số tự nhiên lẻ?
Câu 13:
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) có phương trình\[{x^2} + {y^2} - 2x + 4y - 4 = 0\]và điểm I (2;l). Phép vị tự tâm I tỉ số k = 2 biến đường tròn\[\left( C \right)\]thành đường tròn (C'). Viết phương trình đường tròn\[\left( {C'} \right)\].
Câu 14:
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M, N, I lần lượt là trung điểm của SA, SB, BC; điểm G nằm giữa S và I sao cho\[\frac{{SG}}{{SI}} = \frac{3}{5}\].
a) Tìm giao điểm của đường thẳng MG và mặt phẳng (ABCD).
b) Xác định thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (MNG).
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M, N, I lần lượt là trung điểm của SA, SB, BC; điểm G nằm giữa S và I sao cho\[\frac{{SG}}{{SI}} = \frac{3}{5}\].
a) Tìm giao điểm của đường thẳng MG và mặt phẳng (ABCD).
b) Xác định thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (MNG).
Câu 15:
Cho n là số nguyên dương chẵn bất kì, chứng minh
\[\frac{1}{{1!\left( {n - 1} \right)!}} + \frac{1}{{3!\left( {n - 3} \right)!}} + \frac{1}{{5!\left( {n - 5} \right)!}} + ... + \frac{1}{{\left( {n - 1} \right)!1!}} = \frac{{{2^{n - 1}}}}{{n!}}\]
Cho n là số nguyên dương chẵn bất kì, chứng minh
\[\frac{1}{{1!\left( {n - 1} \right)!}} + \frac{1}{{3!\left( {n - 3} \right)!}} + \frac{1}{{5!\left( {n - 5} \right)!}} + ... + \frac{1}{{\left( {n - 1} \right)!1!}} = \frac{{{2^{n - 1}}}}{{n!}}\]


