30 câu hỏi trắc nghiệm thuộc Dạng 1: dãy số có giới hạn bằng định nghĩa có đáp án

Câu 1:

Chứng minh các dãy số $(u_{n})$ sau đây có giới hạn là 0.

a, $u_{n} = \frac{{(- 1)}^{n}}{3 n + 2} .$

Xem đáp án

a) Với mỗi số dương tùy ý cho trước, ta có

$|u_{n}| = |\frac{{(- 1)}^{n}}{3 n + 2}| = \frac{1}{3 n + 2} < \frac{1}{3 n} < ε$

$\Leftrightarrow n > \frac{1}{3} (\frac{1}{ε} - 2) .$

Đặt $n_{0} = 1 + [\frac{1}{3 ε}]$ thì $n_{0} \in ℕ^{*}$ và $|u_{n}| < ε, \forall n \geq n_{0} .$

Vậy $\lim u_{n} = 0.$

Câu 2:

Chứng minh các dãy số $(u_{n})$ sau đây có giới hạn là 0.

b, $u_{n} = \frac{\sin 4 n}{n + 3} .$

Xem đáp án

b) Ta có $\forall n \in ℕ^{*}$ thì

$|\sin 4 n| \leq 1 \Rightarrow |u_{n}| = |\frac{\sin 4 n}{n + 3}| \leq |\frac{1}{n + 3}| \leq |\frac{1}{n}| = \frac{1}{n} .$

Áp dụng cho định lí “Nếu k là một số thực dương cho trước thì $\lim \frac{1}{n^{k}} = 0$ " ta được $\lim \frac{1}{n} = 0.$

Từ đó suy ra

\lim u_{n} = 0.

Câu 3:

Chứng minh các dãy số $(u_{n})$ sau đây có giới hạn là 0.

$u_{n} = \frac{1 + \sin n^{4}}{4 n + 5} .$

Xem đáp án

Ta có $\forall n \in ℕ^{*}$ thì $|\sin n^{4}| \leq 1 \Rightarrow |u_{n}| = |\frac{1 + \sin n^{4}}{4 n + 5}| \leq |\frac{2}{4 n + 5}| \leq |\frac{2}{4 n}| = \frac{1}{2 n}$ .

Áp dụng định lí “Nếu k là một số thực dương cho trước thì $\lim \frac{1}{n^{k}} = 0$ ” ta được $\lim \frac{1}{n} = 0.$ Từ đó suy ra $\lim u_{n} = 0.$

Câu 4:

Chứng minh các dãy số $(u_{n})$ sau đây có giới hạn là 0.

$u_{n} = \frac{{(- 1)}^{n}}{2^{n + 1}} - \frac{1}{5^{n - 1}} .$

Xem đáp án

Ta có $|u_{n}| = |\frac{{(- 1)}^{n}}{2^{n + 1}} - \frac{1}{5^{n + 1}}| \leq \frac{1}{2^{n + 1}} + \frac{1}{5^{n + 1}} < \frac{1}{2^{n + 1}} + \frac{1}{2^{n + 1}} = \frac{1}{2^{n}}, \forall n \in ℕ .$

Vì $\lim \frac{1}{2^{n}} = \lim {(\frac{1}{2})}^{n} = 0.$

Từ đó suy ra $\lim u_{n} = 0.$

Câu 5:

Chứng minh rằng: $\lim \frac{1}{n + 1} = 0.$

Xem đáp án

Ta có $0 < |\frac{1}{n + 1}| < \frac{1}{n}$ và $\lim \frac{1}{n} = 0.$

Từ đó suy ra điều cần chứng minh.

Câu 6:

Chứng minh rằng các dãy số với số hạng tổng quát sau đây có giới hạn 0.

$u_{n} = (\sqrt{2 n + 3} - \sqrt{2 n}) .$

Xem đáp án

Ta có $(\sqrt{2 n + 3} - \sqrt{2 n}) (\sqrt{2 n + 3} + \sqrt{2 n}) = {(\sqrt{2 n + 3})}^{2} - {(\sqrt{2 n})}^{2} = 3$

$\Rightarrow \sqrt{2 n + 3} - \sqrt{2 n} = \frac{3}{\sqrt{2 n + 3} + \sqrt{2 n}} .$

Mà $\frac{3}{\sqrt{2 n + 3} + \sqrt{2 n}} < \frac{3}{\sqrt{2 n} + \sqrt{2 n}} = \frac{3}{2 \sqrt{2 n}} < \frac{3}{\sqrt{n}}$ và $\lim \frac{3}{\sqrt{n}} = 0.$

Từ đó suy ra điều cần chứng minh.

Câu 7:

Chứng minh rằng các dãy số với số hạng tổng quát sau đây có giới hạn 0.

u_{n} = (\sqrt{n + 2} - \sqrt{n - 2})

Xem đáp án

Ta có $(\sqrt{n + 2} - \sqrt{n - 2}) (\sqrt{n + 2} + \sqrt{n - 2}) = (n + 2) - (n - 2) = 4$

$\Rightarrow \sqrt{n + 2} - \sqrt{n - 2} = \frac{4}{\sqrt{n + 2} + \sqrt{n - 2}} .$

Mà $\frac{4}{\sqrt{n + 2} + \sqrt{n - 2}} < \frac{2}{\sqrt{n - 2}}$ và $\lim \frac{2}{\sqrt{n - 2}} = 0.$

Từ đó suy ra điều cần chứng minh.

Câu 8:

Chứng minh rằng các dãy số với số hạng tổng quát sau có giới hạn 0.

a, $u_{n} = \frac{\cos n}{n + 4} .$

Xem đáp án

a) Ta có $|\frac{\cos n}{n + 4}| < \frac{1}{n + 4} < \frac{1}{n}$ và $\lim \frac{1}{n} = 0.$ Từ đó suy ra điều cần chứng minh.

Câu 9:

Chứng minh rằng các dãy số với số hạng tổng quát sau có giới hạn 0.

c, $u_{n} = \frac{\cos \frac{n π}{5}}{4^{n}} .$

Xem đáp án

b) Ta có $|\frac{{(- 1)}^{n} \cos n}{n^{2} + 1}| < |\frac{\cos n}{n^{2} + 1}| < \frac{1}{n^{2} + 1} < \frac{1}{n^{2}}$ và $\lim \frac{1}{n} = 0.$

Từ đó suy ra điều cần chứng minh.

Câu 10:

Chứng minh rằng các dãy số với số hạng tổng quát sau có giới hạn 0.

c,

u_{n} = \frac{{(- 1)}^{n} \cos n}{n^{2} + 1} .

Xem đáp án

c) Ta có $|\frac{\cos \frac{n π}{5}}{4^{n}}| < \frac{1}{4^{n}} = {(\frac{1}{4})}^{n}$ và $\lim {(\frac{1}{4})}^{n} = 0$ (do $|\frac{1}{4}| < 1$ ).

Từ đó suy ra điều cần chứng minh.

Câu 11:

Chứng minh rằng các dãy số với số hạng tổng quát sau có giới hạn 0.

d,

u_{n} = \frac{\sin \frac{n π}{5}}{{(1, 01)}^{n}}

Xem đáp án

d) Ta có $|\frac{\sin \frac{n π}{5}}{{(1, 01)}^{n}}| < \frac{1}{{(1, 01)}^{n}} = {(\frac{1}{1, 01})}^{n}$ và $\lim {(\frac{1}{1, 01})}^{n} = 0.$

Từ đó suy ra điều cần chứng minh.

Câu 12:

Chứng minh rằng các dãy số sau có giới hạn bằng 0.

a, $\lim \frac{2^{n} + 3^{n}}{4^{n}} = 0.$

Xem đáp án

a) Ta có $\lim \frac{2^{n} + 3^{n}}{4^{n}} = \lim {(\frac{2}{4})}^{n} + \lim {(\frac{3}{4})}^{n} = 0 + 0 = 0$ (do $|\frac{2}{4}| < 1$ và $|\frac{3}{4}| < 1$ ).

Từ đó suy ra điều cần chứng minh.

Câu 13:

Chứng minh rằng các dãy số sau có giới hạn bằng 0.

b, $\lim \frac{a^{n}}{n!} = 0.$

Xem đáp án

b) Gọi m là số tự nhiên thỏa $m + 1 > |a|$ . Khi đó với mọi $n > m + 1.$

Ta có $0 < |\frac{a^{n}}{n!}| = |\frac{a}{1} . \frac{a}{2} ... \frac{a}{m}| . |\frac{a}{m + 1} ... \frac{a}{n}| < \frac{{|a|}^{m}}{m!} . {(\frac{|a|}{m + 1})}^{n - m}$ .

Mà $\lim {(\frac{|a|}{m + 1})}^{n - m} = 0$ và $\frac{{|a|}^{m}}{m!} \leq {|a|}^{m}$ . Từ đó suy ra $\lim \frac{a^{n}}{n!} = 0.$

Câu 14:

Cho dãy số $(u_{n})$ với $u_{n} = \frac{n}{3^{n}} .$

a) Chứng minh rằng $\frac{u_{n + 1}}{u_{n}} \leq \frac{2}{3}$ với mọi n.

Xem đáp án

a) Với mọi n ta có $\frac{u_{n + 1}}{u_{n}} = (\frac{n + 1}{3^{n + 1}}) : (\frac{n}{3^{n}}) = \frac{n + 1}{3 n} \leq \frac{2 n}{3 n} = \frac{2}{3} .$

ta được điều phải chứng minh.

Câu 15:

b) Chứng minh rằng $0 < u_{n} \leq {(\frac{2}{3})}^{n}$ với mọi n.

Xem đáp án

b) Sử dụng phương pháp quy nạp toán học chứng minh $0 < u_{n} \leq {(\frac{2}{3})}^{n}; \forall n (*)$

n=1 ta có $0 < u_{1} = \frac{1}{3} < \frac{2}{3}$ , suy ra (*) đúng với n=1

Giả sử (*) đúng với n=k tức là $0 < \frac{k}{3^{k}} \leq {(\frac{2}{3})}^{k}$ . Ta phải chứng minh (*) đúng với n= k+1

Thật vậy, $u_{k + 1} = \frac{k + 1}{3^{k + 1}} > 0$ . Mặt khác $u_{k + 1} \leq \frac{2}{3} u_{k} \Leftrightarrow u_{k + 1} \leq \frac{2}{3} . {(\frac{2}{3})}^{k} = {(\frac{2}{3})}^{k + 1} .$

Ta được điều phải chứung minh.

Câu 16:

c) Chứng minh rằng dãy số $(u_{n})$ có giới hạn 0.

Xem đáp án

c) Do $0 < u_{n} \leq {(\frac{2}{3})}^{n}$ mà $\lim {(\frac{2}{3})}^{n} = 0$ nên $\lim u_{n} = 0.$

Ta được điều phải chứng minh.

Câu 17:

Tính giới hạn sau: $\lim \frac{1}{n + 1} .$

Xem đáp án

Hướng dẫn giải

Cách bấm máy:

Nhập vào máy tính biểu thức sau:

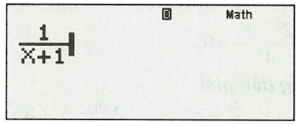
Sau đó bấm CALC, màn hình sẽ xuất hiện như hình bên. Ta hiểu rằng “Bạn muốn gán x bằng bao nhiêu?”

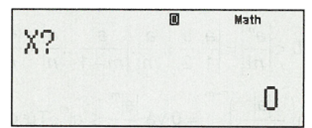
Nhập: $x = 9999999999$ , sau đó bấm “=”, ta được kết quả:

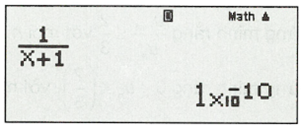
Câu 18:

Tính giới hạn sau: $\lim \frac{{(- 1)}^{n}}{n + 5}$ .

Xem đáp án

Nhập vào máy tính biểu thức sau:

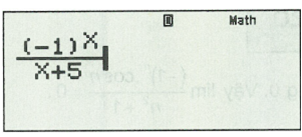
Sau đó bấm CALC.

Tính giới hạn sau: lim (-1)^n /n +5. (ảnh 2)

Nhập $x = 9999999999$ , sau đó bấm “=”, ta được kết quả:

Tính giới hạn sau: lim (-1)^n /n +5. (ảnh 3)

Kết quả: $- 9, {999999996.10}^{- 11}$ là một giá trị rất nhỏ gần bằng 0.

Vậy $\lim \frac{{(- 1)}^{n}}{n + 5} = 0.$

Câu 19:

Tính giới hạn sau: $\lim \frac{{(- 1)}^{n} . \cos n}{n^{2} + 1} .$

Xem đáp án

Nếu ta nhập $\frac{{(- 1)}^{n} . \cos n}{n^{2} + 1}$ , sau đó CALC như trên máy sẽ báo: MATH ERROR.

Hướng dẫn giải

Vận dụng định lí 1 nếu $|u_{n}| \leq v_{n}$ với mọi n và $\lim v_{n} = 0$ thì $\lim u_{n} = 0.$

Ta có đánh giá sau: $|\frac{{(- 1)}^{n} . \cos n}{n^{2} + 1}| < |\frac{\cos n}{n^{2} + 1}| < \frac{1}{n^{2} + 1}$ , ta chỉ cần ghi $\frac{1}{n^{2} + 1}$ vào máy tính là sẽ tính được.

Cách bấm máy:

Nhập vào máy tính biểu thức sau:

Tính giới hạn sau: lim (-1)^n. cosn /n^2+1 (ảnh 1)

Sau đó bấm CALC.

Tính giới hạn sau: lim (-1)^n. cosn /n^2+1 (ảnh 2)

Nhập: $x = 9999999999$ , sau đó bấm “=”, ta được kết quả:

Tính giới hạn sau: lim (-1)^n. cosn /n^2+1 (ảnh 3)

Kết quả: ${1.10}^{- 20}$ là một giá trị rất rất nhỏ gần bằng 0. Vậy $\lim \frac{{(- 1)}^{n} . \cos n}{n^{2} + 1} = 0.$

Câu 20:

Tính giới hạn sau

\lim \frac{{(- 1)}^{n}}{2^{n} + 1} .

Xem đáp án

Nếu ta nhập $\frac{{(- 1)}^{n}}{2^{n} + 1}$ , sau đó CALC như trên máy sẽ báo: MATH ERROR do hàm số mũ tăng rất nhanh nên sẽ không tính được trên máy tính. Trong trường hợp này ta sẽ xử lý như sau:

Hướng dẫn giải

Cách bấm máy:

Nhập vào máy tính biểu thức sau:

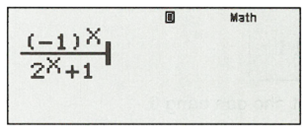
Tính giới hạn sau lim (-1)^n/ 2^n +1 (ảnh 1)

Bấm CALC.

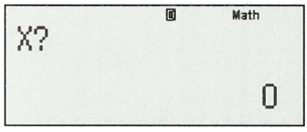
Tính giới hạn sau lim (-1)^n/ 2^n +1 (ảnh 2)

Nhâp: x=100, sau đó bấm “=”, ta được kết quả:

Tính giới hạn sau lim (-1)^n/ 2^n +1 (ảnh 3)

Kết quả: $7, {888609052.10}^{- 31}$ là một giá trị rất rất nhỏ gần bằng 0.

Vậy $\lim \frac{{(- 1)}^{n}}{2^{n} + 1} = 0.$

Câu 21:

Trong các dãy số sau, dãy số nào có giới hạn 0?

A. $u_{n} = {(- \frac{3}{2})}^{n} .$

B. $u = {(- \sqrt{2})}^{n} .$

C. $u_{n} = {(\frac{4}{2 + \sqrt{5}})}^{n} .$

D. $u_{n} = {(- \frac{2 + \sqrt{5}}{4})}^{n} .$

Xem đáp án

Ta có $|\frac{4}{2 + \sqrt{5}}| < 1$ nên $\lim {(\frac{4}{2 + \sqrt{5}})}^{n} = 0.$

Chọn đáp án C

Câu 22:

Dãy số với $u_{n} = \frac{(- 1) . \cos 5 n}{3^{n}}$ có giới hạn bằng

A. $\frac{1}{3} .$

B. -1

C. $\frac{- 1}{3} .$

D. 0

Xem đáp án

Ta có $0 \leq |\frac{(- 1) . \cos 5 n}{3^{n}}| = |\frac{\cos 5 n}{3^{n}}| < \frac{1}{3^{n}} = {|\frac{1}{3}|}^{n}$ mà $\lim \frac{1}{3^{n}} = 0$ nên $\lim \frac{{(- 1)}^{n + 1}}{3^{n} + 5} = 0.$

Chọn đáp án D

Câu 23:

Giới hạn

\lim \frac{\sin \frac{π n}{6}}{3 n^{2} + 1}

bằng

A. 0

B. 1

C. $\frac{- 1}{3}$

D. $\frac{1}{3}$

Xem đáp án

Ta có $0 \leq |\frac{\sin \frac{π n}{6}}{3 n^{2} + 1}| < \frac{1}{3 n^{2} + 1} < \frac{1}{3 n^{2}}$ mà $\lim \frac{1}{3 n^{2}} = 0$ nên $\lim \frac{\sin \frac{π n}{6}}{3 n^{2} + 1} = 0.$

Câu 24:

Giới hạn $\lim \frac{{(- 1)}^{n + 1}}{3^{n} + 5}$ bằng

A. $\frac{1}{5}$

B. $\frac{- 1}{5}$

C. $\frac{1}{3}$

D. 0

Xem đáp án

Ta có $0 \leq |\frac{{(- 1)}^{n + 1}}{3^{n} + 5}| = |\frac{{(- 1)}^{n}}{3^{n} + 5}| < \frac{1}{3^{n} + 5} < \frac{1}{3^{n}}$ mà $\lim \frac{1}{3^{n}} = 0$ nên $\lim \frac{{(- 1)}^{n + 1}}{3^{n} + 5} = 0.$

Chọn đáp án D

Câu 25:

Giới hạn

\lim (2 + \frac{{(- 1)}^{n}}{n + 2})

là

A. 2

B. $\frac{1}{2}$

C. 0

D. 1

Xem đáp án

Chọn đáp án A

Ta có $(2 + \frac{{(- 1)}^{n}}{n + 2}) - 2 = \frac{{(- 1)}^{n}}{n + 2}$ mà $|\frac{{(- 1)}^{n}}{n + 2}| < \frac{1}{n}, \forall n$ và $\lim \frac{1}{n} = 0.$

Suy ra

\lim [(2 + \frac{{(- 1)}^{n}}{n + 2}) - 2] = 0 \Rightarrow \lim (2 + \frac{{(- 1)}^{n}}{n + 2}) = 2.

Câu 26:

Giới hạn $\lim \frac{n^{2} - n + 3}{n^{3} + 2 n}$ bằng

A. $\frac{1}{3}$

B. 0

C. $\frac{1}{2}$

D. $\frac{- 1}{2}$

Xem đáp án

Ta có $\frac{n^{2} - n + 3}{n^{3} + 2 n} = \frac{n^{2} (1 - \frac{1}{n} + \frac{3}{n^{2}})}{n^{3} (1 + \frac{2}{n^{2}})} = \frac{1}{n} . \frac{1 - \frac{1}{n} + \frac{3}{n^{2}}}{1 + \frac{2}{n^{2}}}$ mà $\lim \frac{1}{n} = 0; \lim \frac{1 - \frac{1}{n} + \frac{3}{n^{2}}}{1 + \frac{2}{n^{2}}} = 1.$

Suy ra $\lim \frac{n^{2} - n + 3}{n^{3} + 2 n} = 0.$

Chọn đáp án B

Câu 27:

Trong các dãy số dưới đây, dãy số nào có giới hạn 0?

(1): $\frac{{(- 1)}^{n}}{n + 5};$ (2): $\frac{\sin n}{n + 5};$ (3): $\frac{\cos 2 n}{\sqrt{n} + 1};$ (4): $\frac{n^{2} + 2}{n (n + 1)};$ (5): $\frac{{(- 1)}^{n} . \cos n}{n^{2} + 2} .$

A. (1), (2), (3), (4).

B. Chỉ (2), (3).

C. (1), (2), (3), (5).

D. Chỉ (1), (5).

Xem đáp án

Dễ dàng nhận thấy các các phương án (1); (2); (3); (5) đều có giới hạn là 0, bạn đọc có thể tự chứng minh.

Ta xét phương án:

(4): $\frac{n^{2} + 2}{n (n + 1)} = \frac{n^{2} + 2}{n^{2} + 1} = \frac{n^{2} (1 + \frac{2}{n^{2}})}{n^{2} (1 + \frac{1}{n^{2}})} = \frac{1 + \frac{2}{n^{2}}}{1 + \frac{1}{n^{2}}},$ mà $\lim \frac{1 + \frac{2}{n^{2}}}{1 + \frac{1}{n^{2}}} = 1.$

Vậy phương án (4) không thỏa mãn.

Chọn đáp án C

Câu 28:

Xét các câu sau:

(1) Ta có $\lim {(\frac{1}{3})}^{n} = 0;$

(2) Ta có $\lim \frac{1}{n^{k}} = 0$ , với k là số nguyên tùy ý.

A. Cả hai câu đều đúng.

B. Cả hai câu đều sai.

C. Chỉ (1) đúng.

D. Chỉ (2) sai.

Xem đáp án

Dễ dàng nhận thấy phương án (1) hoàn toàn chính xác do: $|\frac{1}{3}| < 1$ nên $\lim {(\frac{1}{3})}^{n} = 0.$

Phương án (2) là sai, vì $\lim \frac{1}{n^{k}} = 0$ khi k là số nguyên dương $(k \in ℤ^{+})$ . Vậy phương án (2) sai.

Câu 29:

Cho dãy số $(u_{n})$ được xác định $\{\begin{cases} u_{n} = m, (m \geq 1) \\ 2^{n} u_{n + 1} = |2^{n} u_{n} - 1|, n \in ℕ^{*} \end{cases} .$

Tham số m để dãy số $(u_{n})$ có giới hạn bằng 0 là

A. m=1

B. m=2

C. m=3

D. m=4

Xem đáp án

Chọn đáp án C

Ta có $2^{n} u_{n + 1} = |2^{n} . u_{n} - 1| \Leftrightarrow u_{n + 1} = |u_{n} - \frac{1}{2^{n}}| .$

Chứng minh: $u_{n} \geq 2^{1 - n}$ (bằng quy nạp).

* Với n=1 ta có $u_{1} = m \geq 1 = 2^{0} .$

* Giả sử $u_{k} > 2^{1 - k}$ (với k>1)

* Cần chứng minh: $u_{k + 1} > 2^{- k} .$

Ta có $u_{k + 1} = |u_{k} - 2^{- k}| > |2^{1 - k} - 2^{- k}| = 2^{- k}$ . Suy ra điều phải chứng minh.

Từ đó suy ra $u_{n} - 2^{- n} > 0$ với mọi $n \Rightarrow u_{n + 1} = u_{n} - \frac{1}{2^{n}} .$

Ta có $u_{2} = u_{1} - \frac{1}{2}; u_{3} = u_{2} - \frac{1}{2^{2}}; u_{4} = u_{3} - \frac{1}{2^{3}}; ...; u_{n} = u_{n - 1} - \frac{1}{2^{n - 1}}$

$\Rightarrow u_{n} = u_{1} - (\frac{1}{2} + \frac{1}{2^{2}} + \frac{1}{2^{3}} + ... + \frac{1}{2^{n - 1}}) .$

Công thức tổng quát $u_{n} = m - \frac{1}{2} . \frac{1 - {(\frac{1}{2})}^{n - 1}}{\frac{1}{2}} = m - 1 + {(\frac{1}{2})}^{n - 1}$

$\Rightarrow \lim u_{n} = 0 \Leftrightarrow \lim (m - 1) + \lim {(\frac{1}{2})}^{n - 1} = 0$

Câu 30:

Dãy số nào sau đây có giới hạn khác 0?

A. $\frac{\cos n}{\sqrt{n}} .$

B. $\frac{1}{\sqrt{n}} .$

C. $\frac{2 n + 1}{n} .$

D. $\frac{1}{n} .$

Xem đáp án

Chọn đáp án C

Dễ dàng chứng minh được các đáp án A, B và D có giới hạn là 0, bạn đọc có thể tự chứng minh.

Ta xét phương án C:

$\frac{2 n + 1}{n} = \frac{n (2 + \frac{1}{n})}{n} = 2 + \frac{1}{n}$ , mà $\lim (2 + \frac{1}{n}) = 2 \neq 0$ . Vậy phương án C không thỏa mãn.

Bài tập chuyên đề Toán 11 Bài 1: Giới hạn của dãy số có đáp án

Dạng 1: dãy số có giới hạn bằng định nghĩa có đáp án

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương