24 câu hỏi trắc nghiệm thuộc Dạng 3: Dãy số có giới hạn vô cực có đáp án

Bài tập chuyên đề Toán 11 Bài 1: Giới hạn của dãy số có đáp án

Dạng 3: Dãy số có giới hạn vô cực có đáp án

967 lượt thi
24 câu hỏi
0 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Tìm các giới hạn sau:

a) $\lim \frac{n^{5} + n^{4} - n - 2}{4 n^{3} + 6 n^{2} + 9}$

Hướng dẫn giải

a) $\lim \frac{n^{5} + n^{4} - n - 2}{4 n^{3} + 6 n^{2} + 9} = \lim \frac{n^{5} (1 + \frac{1}{n} - \frac{1}{n^{4}} - \frac{2}{n^{5}})}{n^{3} (4 + \frac{6}{n} + \frac{9}{n^{3}})} .$

$= \lim n^{2} . (\frac{1 + \frac{1}{n} - \frac{1}{n^{4}} - \frac{2}{n^{5}}}{4 + \frac{6}{n} + \frac{9}{n^{3}}}) .$

Mà $\lim n^{2} = + \infty$ và $\lim (\frac{1 + \frac{1}{n} - \frac{1}{n^{4}} - \frac{2}{n^{5}}}{4 + \frac{6}{n} + \frac{9}{n^{3}}}) = \frac{1}{4} > 0$

Nên $\lim \frac{n^{5} + n^{4} - n - 2}{4 n^{3} + 6 n^{2} + 9} = + \infty .$

Câu 2:

Tìm các giới hạn sau: b, $\lim \frac{- \sqrt[3]{n^{6} - 7 n^{3} - 5 n + 8}}{n + 12}$

b)

$\lim \frac{- \sqrt[3]{n^{6} - 7 n^{3} - 5 n + 8}}{n + 12}$

$= \lim \frac{- n^{2} . \sqrt[3]{1 - \frac{7}{n^{3}} - \frac{5}{n^{5}} + \frac{8}{n^{6}}}}{n (1 + \frac{12}{n})}$

$= \lim (- n) . \frac{\sqrt[3]{1 - \frac{7}{n^{3}} - \frac{5}{n^{5}} + \frac{8}{n^{6}}}}{1 + \frac{12}{n}}$

Mà $\lim (- n) = - \infty$ và $\lim \frac{\sqrt[3]{1 - \frac{7}{n^{3}} - \frac{5}{n^{5}} + \frac{8}{n^{6}}}}{1 + \frac{12}{n}} = \frac{1}{1} = 1 > 0$

Nên

$\lim \frac{- \sqrt[3]{n^{6} - 7 n^{3} - 5 n + 8}}{n + 12} = - \infty .$

Câu 3:

Tìm các giới hạn sau:

$\lim (\sqrt{2 n + 3} - \sqrt{n + 1}) .$

Hướng dẫn giải

a) $\lim (\sqrt{2 n + 3} - \sqrt{n + 1}) = \lim \sqrt{n} . (\sqrt{2 + \frac{3}{n}} - \sqrt{1 + \frac{1}{n}}) .$

Do $\lim \sqrt{n} = + \infty$ và $\lim (\sqrt{2 + \frac{3}{n}} - \sqrt{1 + \frac{1}{n}}) = \sqrt{2} - 1 > 0.$

Nên $\lim (\sqrt{2 n + 3} - \sqrt{n + 1}) = + \infty$ .

Câu 4:

Tìm các giới hạn sau:

b, $\lim \frac{(n^{2} + 1) (2 n + 3)}{\sqrt{n^{4} - n^{2} + 1}} .$

b)

$\lim \frac{(n^{2} + 1) (2 n + 3)}{\sqrt{n^{4} - n^{2} + 1}} = \lim \frac{(1 + \frac{1}{n^{2}}) (2 + \frac{3}{n})}{\sqrt{\frac{1}{n^{2}} - \frac{1}{n^{4}} + \frac{1}{n^{6}}}} .$

Do $\lim (1 + \frac{1}{n^{2}}) (2 + \frac{3}{n}) = 1.2 = 2 > 0; \lim \sqrt{\frac{1}{n^{2}} - \frac{1}{n^{4}} + \frac{1}{n^{6}}} = 0$ và $\sqrt{\frac{1}{n^{2}} - \frac{1}{n^{4}} + \frac{1}{n^{6}}} > 0.$

Nên

$\lim \frac{(n^{2} + 1) (2 n + 3)}{\sqrt{n^{4} - n^{2} + 1}} = + \infty .$

Câu 5:

Tìm các giới hạn sau:

a, $\lim (5^{n} - 3^{n + 1}) .$

Hướng dẫn giải

a) $\lim (5^{n} - 3^{n + 1}) = \lim 5^{n} . [1 - 3. {(\frac{3}{5})}^{n}] .$

Do $\lim 5^{n} = + \infty$ và $\lim [1 - 3. {(\frac{3}{5})}^{n}] = 1 - 3.0 = 1 > 0$ nên $\lim (5^{n} - 3^{n + 1}) = + \infty$ .

Câu 6:

Tìm các giới hạn sau:

b, $\lim \frac{{(- 3)}^{n} - 6^{n}}{{(- 3)}^{n + 1} + 5^{n + 1}} .$

b) $\lim \frac{{(- 3)}^{n} - 6^{n}}{{(- 3)}^{n + 1} + 5^{n + 1}} = \lim \frac{{(- \frac{1}{2})}^{n} - 1}{3 {(- \frac{1}{2})}^{n} + 5 {(\frac{5}{6})}^{n}} .$

Do $\lim [{(- \frac{1}{2})}^{n} - 1] = - 1 < 0; \lim [3 {(- \frac{1}{2})}^{n} + 5 {(\frac{5}{6})}^{n}] = 0$ và $3 {(- \frac{1}{2})}^{n} + 5 {(\frac{5}{6})}^{n} > 0$

Nên $\lim \frac{{(- 3)}^{n} - 6^{n}}{{(- 3)}^{n + 1} + 5^{n + 1}} = - \infty .$

Câu 7:

Tìm các giới hạn sau:

$\lim (\sqrt{n^{4} + 1} + n - 1) .$

Hướng dẫn giải

a) $\lim (\sqrt{n^{4} + 1} + n - 1) = \lim n^{2} (\sqrt{1 + \frac{1}{n^{4}}} + \frac{1}{n} - \frac{1}{n^{2}}) .$

Do $\lim n^{2} = + \infty$ và $\lim (\sqrt{1 + \frac{1}{n^{4}}} + \frac{1}{n} - \frac{1}{n^{2}}) = 1 > 0$ nên $\lim (\sqrt{n^{4} + 1} + n - 1) = + \infty .$

Câu 8:

Tìm các giới hạn sau: b, $\lim (\frac{1}{3} n^{3} + 2 \sin 2 n + 3) .$

b) $\lim (\frac{1}{3} n^{3} + 2 \sin 2 n + 3) = \lim n^{3} (\frac{1}{3} + \frac{2 \sin 2 n}{n^{3}} + \frac{3}{n^{3}}) .$

Mà $\lim n^{3} = + \infty$ và $\lim (\frac{1}{3} + \frac{2 \sin 2 n}{n^{3}} + \frac{3}{n^{3}}) = \frac{1}{3} + 0 + 0 = \frac{1}{3} > 0.$

(do $|\frac{2 \sin 2 n}{n^{3}}| \leq \frac{2}{n^{3}}, \forall n; \lim \frac{2}{n^{3}} = 0 \Rightarrow \lim \frac{2 \sin 2 n}{n^{3}} = 0$ )

Nên $\lim (\frac{1}{3} n^{3} + 2 \sin 2 n + 3) = + \infty .$

Câu 9:

Tính giới hạn sau:

$\lim \frac{4 n^{4} - n^{2} + 1}{(2 n + 1) (3 - n) (n^{2} + 1)} .$

Hướng dẫn giải

Cách bấm máy:

Nhập vào máy tính biểu thức sau:

Tính giới hạn sau: lim 4n^4 -n^2+1/ (2n+1)(3-n)(n^2+1) (ảnh 1)

Sau đó bấm CALC.

Tính giới hạn sau: lim 4n^4 -n^2+1/ (2n+1)(3-n)(n^2+1) (ảnh 2)

Nhập: $x = 9999999999$ , sau đó bấm “=”, ta được kết quả:

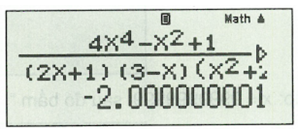
Tính giới hạn sau: lim 4n^4 -n^2+1/ (2n+1)(3-n)(n^2+1) (ảnh 3)

Kết quả: Vậy giới hạn của dãy số bằng -2

Câu 10:

Tính giới hạn sau: $\lim \frac{\sqrt{9 n^{2} - n + 1}}{4 n - 2} .$

Hướng dẫn giải

Cách bấm máy:

Nhập vào máy tính biểu thức sau:

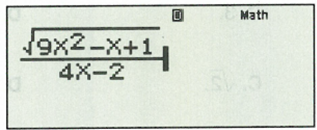
Tính giới hạn sau: lim căn 9n^2 -n +1/ 4n -2 (ảnh 1)

Sau đó bấm CALC.

Tính giới hạn sau: lim căn 9n^2 -n +1/ 4n -2 (ảnh 2)

Nhập: $x = 9999999999$ , sau đó bấm “=”, ta được kết quả:

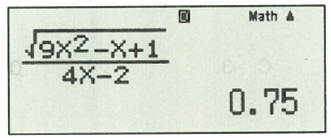
Tính giới hạn sau: lim căn 9n^2 -n +1/ 4n -2 (ảnh 3)

Kết quả: Vậy giới hạn của dãy số bằng $0, 75 = \frac{3}{4} .$

Câu 11:

Tính giới hạn sau: $\lim \frac{1}{\sqrt{n + 2} - \sqrt{n + 1}} .$

Hướng dẫn giải

Cách bấm máy:

Nhập vào máy tính biểu thức sau:

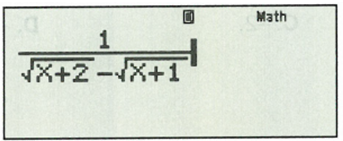
Tính giới hạn sau: lim 1/ căn n+2 - căn n+1 (ảnh 1)

Sau đó bấm CALC.

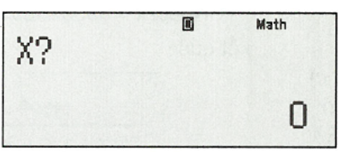
Tính giới hạn sau: lim 1/ căn n+2 - căn n+1 (ảnh 2)

Nhập $x = 9999999999$ , sau đó bấm “=”, ta được kết quả:

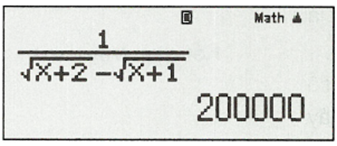
Tính giới hạn sau: lim 1/ căn n+2 - căn n+1 (ảnh 3)

Kết quả: Vậy giới hạn của dãy số bằng $+ \infty .$

Câu 12:

Giới hạn $\lim (2 n^{2} - n + 1)$ bằng

A. $- \infty .$

B. 2

C. -2

D. $+ \infty .$

Ta có $\lim (- n^{3} + 2 n^{2} + 2) = \lim n^{3} (- 1 + \frac{2}{n} + \frac{2}{n^{3}}) = - \infty .$

Chọn đáp án A

Câu 13:

Giá trị của

$\lim (- n^{3} + 2 n^{2} + 2)$ bằng

A. $- \infty .$

B. -3

C.3

D. $+ \infty .$

Ta có $\lim \sqrt{2 n^{2} - 3 n - 8} = \lim n \sqrt{2 - \frac{3}{n} - \frac{8}{n^{2}}} = + \infty .$

Chọn đáp án D

Câu 14:

$\lim \sqrt{2 n^{2} - 3 n - 8}$ bằng

A. $2 \sqrt{2} .$

B. $\sqrt{3}$

C. $\sqrt{2}$

D. $+ \infty .$

Ta có

$\lim \sqrt{2 n^{2} - 3 n - 8} = \lim n \sqrt{2 - \frac{3}{n} - \frac{8}{n^{2}}} = + \infty .$

Chọn đáp án D

Câu 15:

Giá trị của

$\lim n \sqrt{n + 1}$ bằng

A. $- \infty .$

B. 1

C. -1

D. $+ \infty .$

Ta có $\lim n \sqrt{n + 1} = \lim n \sqrt{n} (\sqrt{1 + \frac{1}{n}}) = + \infty .$

Chọnn đáp án D

Câu 16:

Giới hạn $\lim (- 2 n^{2} + 5 n) (3^{n} - 2^{n})$ bằng

A. $- \infty$

B. 5

C. -5

D. $+ \infty$

Ta có $\lim (- 2 n^{2} + 5 n) = \lim n^{2} (- 2 + \frac{5}{n}) = - \infty$ và $\lim (3^{n} - 2^{n}) = \lim 3^{n} (1 - {(\frac{2}{3})}^{n}) = + \infty .$

Nên

$\lim (- 2 n^{2} + 5 n) (3^{n} - 2^{n}) = - \infty .$ Chọn đáp án A

Câu 17:

$\lim \frac{3 n^{3}}{- n^{2} + 1}$ bằng

A. $- \infty$

B. 3

C. -3

D. $+ \infty$

Ta có

$\lim \frac{3 n^{3}}{- n^{2} + 1} = \lim \frac{3 n}{- 1 + \frac{1}{n^{2}}} = \lim \frac{3 n}{- 1} = \lim (- 3 n) = - \infty .$

Chọn đáp án A

Câu 18:

Giới hạn $\lim \frac{2 n^{2} - 3 n + 1}{n + 1}$ bằng

A. - $\infty$

B. 3

C. -3

D. $+ \infty$

Ta có $\lim \frac{2 n^{2} - 3 n + 1}{n + 1} = \lim \frac{2 - \frac{3}{n} + \frac{1}{n^{2}}}{\frac{1}{n} + \frac{1}{n^{2}}} .$ Do $\lim (2 - \frac{3}{n} + \frac{1}{n^{2}}) = 2$ và $\lim (\frac{1}{n} + \frac{1}{n^{2}}) = 0$ mà $\frac{1}{n} + \frac{1}{n^{2}} > 0.$

Nên

$\lim \frac{(2 - \frac{3}{n} + \frac{1}{n^{2}})}{\frac{1}{n} + \frac{1}{n^{2}}} = + \infty .$

Chọn đáp án D

Câu 19:

Giá trị của

$\lim n (\sqrt{n + \sqrt{n + \sqrt{n}}} - \sqrt{n})$ bằng

A. $- \infty$

B. $+ \infty$

C. -1

D. $\frac{1}{2}$

Ta có

$\lim n (\sqrt{n + \sqrt{n + \sqrt{n}}} - \sqrt{n}) = \frac{1}{2} .$ Chọn đáp án D

Câu 20:

Giá trị của $\lim n (\sqrt{n^{2} + 2 n + 3} - \sqrt[3]{n + n^{3}})$ bằng

A. $- \infty$

B. $\frac{1}{2}$

C. -2

D. $+ \infty$

Ta có $\lim n = + \infty$ và

$\lim (\sqrt{n^{2} + 2 n + 3} - n + n - \sqrt[3]{n + n^{3}}) = \lim (\frac{2 n + 3}{\sqrt{n^{2} + 2 n + 3} + n}) + \lim (\frac{- n}{n^{2} + n . \sqrt[3]{n + n^{3}} + {(\sqrt[3]{n + n^{3}})}^{2}}) = 1.$

Vậy $\lim n (\sqrt{n^{2} + 2 n + 3} - \sqrt[3]{n + n^{3}}) = + \infty .$

Chọn đáp án D

Câu 21:

Giới hạn $\lim \frac{n \sqrt{2 n^{2} - 1}}{\sqrt[3]{n^{2} + 2 n}}$ bằng

A. - $\infty$

B. 2

C. 3

D. $+ \infty$

Ta có $L = \lim \frac{n \sqrt{2 n^{2} - 1}}{\sqrt[3]{n^{2} + 2 n}} = \lim \frac{n^{2} . \sqrt{2 - \frac{1}{n^{2}}}}{\sqrt[3]{n^{2} (\frac{n^{2} + 2 n}{n^{2}})}} = \lim \frac{{(\sqrt[3]{n^{2}})}^{3} . \sqrt{2 - \frac{1}{n^{2}}}}{\sqrt[3]{n^{2}} . \sqrt[3]{1 + \frac{2}{n^{2}}}} = \lim [{(\sqrt[3]{n^{2}})}^{2} . \frac{\sqrt{2 - \frac{1}{n^{2}}}}{\sqrt[3]{1 + \frac{2}{n^{2}}}}]$

Do $\lim [\frac{\sqrt{2 - \frac{1}{n^{2}}}}{\sqrt[3]{1 + \frac{2}{n^{2}}}}] = \sqrt{2}$ và $\lim {(\sqrt[3]{n^{2}})}^{2} = + \infty$ nên $L = + \infty$ .

Chọn đáp án D

Câu 22:

Giới hạn $\lim \frac{\sqrt[3]{n^{6} - 7 n^{3} - 5 n + 8}}{n + 2}$ bằng

A. $- \infty$

B. -7

C. 1

D. $+ \infty$

Ta có

$L = \lim \frac{\sqrt[3]{n^{6} - 7 n^{3} - 5 n + 8}}{n + 2} = \lim \frac{\sqrt[3]{n^{6} . \frac{n^{6} - 7 n^{3} - 5 n + 8}{n^{6}}}}{n + 2} = \lim \frac{n^{2} . \sqrt[3]{1 - \frac{7}{n^{3}} - \frac{5}{n^{5}} + \frac{8}{n^{6}}}}{n + 2} = \lim (n . \frac{\sqrt[3]{1 - \frac{7}{n^{3}} - \frac{5}{n^{5}} + \frac{8}{n^{6}}}}{1 + \frac{2}{n}})$

Ta có $\lim (\frac{\sqrt[3]{1 - \frac{7}{n^{3}} - \frac{5}{n^{5}} - \frac{8}{n^{6}}}}{1 + \frac{2}{n}}) = 1$ và $\lim n = + \infty .$

Từ đó suy ra $L = + \infty .$ Chọn đáp án D

Câu 23:

$\lim \frac{n \cos \frac{π}{n}}{n^{2} + 1}$ bằng

A. 5

B. 0

C. -2

D. $+ \infty$

Ta có $|\frac{n \cos \frac{π}{n}}{n^{2} + 1}| \leq \frac{n}{n^{2} + 1}$ và $\lim \frac{n}{n^{2} + 1} = 0$ nên $\lim \frac{n \cos \frac{π}{n}}{n^{2} + 1} = 0.$

Chọn đáp án B

Câu 24:

Giới hạn bằng

A. $- \infty$

B. -5

C. 5

D. $+ \infty$

Ta có

$\lim (\frac{\sin n^{2}}{\sqrt{n}} - 5) = - 5.$

Chọn đáp án B

Bắt đầu thi ngay

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương