Dạng 1: Hàm số liên tục tại một điểm, trên một tập có đáp án
-
184 lượt thi
-
33 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Cho hàm số
Xét tính liên tục của hàm số tại điểm x=3
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Hàm số xác định trên R
Ta có và
Câu 2:
Cho hàm số . Xét tính liên tục của hàm số tại điểm x=3
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Ta có
Do đó
Vậy hàm số gián đoạn tại x=3
Câu 3:
Cho hàm số . Tìm a để hàm số liên tục tại điểm x=2
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Hàm số xác định trên R
Ta có và
Vậy để hàm số liên tục tại điểm x=2 thì
Câu 4:
Cho hàm số
Tìm m để hàm số liên tục tại điểm x=-1
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Hàm số xác định trên R
Ta có:
Hàm số liên tục tại x=-1 khi và chỉ khi
Câu 5:
Xét tính liên tục của hàm số trên toàn bộ tập xác định
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Hàm số xác định trên D=R
Với thì là hàm số liên tục trên tập xác định.
Do đó hàm số liên tục trên và
Với x= -1 ta có
Vì
Vậy hàm số liên tục trên các khoảng và ; hàm số không liên tục tại điểm x=-1
Câu 6:
Cho hàm số
Tìm a để hàm số liên tục trên tập xác định Xem đáp án
Xem đáp án
Hướng dẫn giải
Hàm số xác định trên R
Với x>2 ta có là hàm số liên tục trên từng khoảng xác định.
Do đó hàm số f(x) liên tục trên
Với x<2 ta có là hàm số liên tục trên tập xác định. Do đó hàm số f(x) liên tục trên
Với x=2 ta có
Hàm số liên tục trên khi và chỉ khi hàm số liên tục tại x=2 , nên
Vậy là những giá trị cần tìm.
Câu 7:
Hàm số có đồ thị như hình bên gián đoạn tại điểm có hoành độ bằng bao nhiêu?
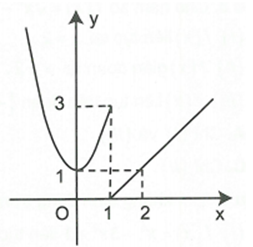
 Xem đáp án
Xem đáp án
Dựa vào hình vẽ đồ thị ta thấy hàm số gián đoạn tại điểm x=1
Câu 8:
Cho hàm số f(x) có đồ thị như hình bên. Chọn khẳng định đúng.
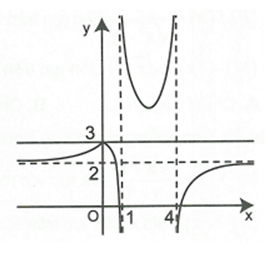
 Xem đáp án
Xem đáp án
Dựa vào hình vẽ đồ thị ta thấy hàm số liên tục trên (1, 4)
Câu 9:
Hàm số liên tục trên khoảng nào sau đây?
 Xem đáp án
Xem đáp án
Điều kiện xác định của hàm số
Do đó hàm số đã cho gián đoạn tại điểm có hoành độ bằng -2 và -3
Câu 10:
Cho hàm số . Khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
Hàm số xác định trên R
Ta có:
Suy ra
Vậy hàm số đã cho liên tục trên nửa khoảng và khoảng
Câu 11:
Giá trị của a để các hàm số liên tục tại x=0 bằng
 Xem đáp án
Xem đáp án
Hàm số xác định trên R
Ta có:
Hàm số đã cho liên tục tại điểm x=0 khi và chỉ khi
Câu 12:
 Xem đáp án
Xem đáp án
Hàm số xác định trên R
Ta có:
Hàm số đã cho liên tục tại điểm khi và chỉ khi
Câu 13:
Cho hàm số . Tìm k để f(x) gián đoạn tại x=1
 Xem đáp án
Xem đáp án
Hàm số xác định trên R
Ta có:
Vậy hàm số đã cho gián đoạn tại x=1 khi và chỉ khi
Câu 14:
Cho hàm số . Tìm khẳng định đúng trong các khẳng định sau:
(I) liên tục tại x=2
(II) gián đoạn tại x=2
(III) liên tục trên đoạn
 Xem đáp án
Xem đáp án
Điều kiện xác định:
Ta có: . Do đó hàm số đã cho liên tục tại x=2
. Do đó hàm số đã cho liên tục tại x=-2
Câu 15:
Tìm khẳng định đúng trong các khẳng định sau
(I) liên tục trên
(II) liên tục trên
(III) liên tục trên
 Xem đáp án
Xem đáp án
(I) là hàm số có tập xác định trên R. Do đó hàm số f(x) liên tục trên R
(II) có tập xác định .
Do đó f(x) gián đoạn trên khoảng
(III) Hàm số có tập xác định
Ta có: . Do đó hàm số liên tục trên
Câu 16:
Cho hàm số Khẳng định nào sau đây đúng nhât?
 Xem đáp án
Xem đáp án
Khi đó ta có
Suy ra
Do đó hàm số liên tục tại x=-1
+) . Suy ra . Do đó hàm số liên tục tại x=1
Câu 17:
Cho hàm số . Tìm khẳng định đúng trong các khẳng định sau:
(I) f(x) liên tục tại
(II) f(x) gián đoạn tại
(III) f(x) liên tục trên R
 Xem đáp án
Xem đáp án
Tập xác định: D= R
Ta có:
Do đó hàm số liên tục tại . Vậy hàm số liên tục trên R
Câu 18:
Hàm số nào sau đây không liên tục tại x=1
 Xem đáp án
Xem đáp án
Xét có tập xác định D=R
Ta có
Suy ra
Do đó hàm số gián đoạn tại điểm x=1
Câu 19:
liên tục tại x=0
 Xem đáp án
Xem đáp án
Ta có
Hàm số liên tục tại x=0 khi và chỉ khi
Câu 20:
Cho hàm số . Khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
Ta có nên hàm số liên tục tại x=1
Ta cũng ó\có nên hàm số liên tục tại x=0
Câu 21:
Cho hàm số
Tìm các giá trị của tham số thực m để hàm số liên tục trên R
 Xem đáp án
Xem đáp án
Ta có:
Hàm số f(x) liên tục trên R khi và chỉ khi hàm số f(x) liên tục tại x=2
Câu 22:
Giá trị a để các hàm số liên tục tại điểm x=0 là
 Xem đáp án
Xem đáp án
Ta có
Suy ra thì hàm số liên tục tại điểm x=0
Câu 23:
Giá trị của a để các hàm số liên tục tại điểm x=1 là
 Xem đáp án
Xem đáp án
Ta có
Vậy thì hàm số liên tục tại x=1
Câu 24:
Giá trị của a để hàm số liên tục tại điểm x=0 là
 Xem đáp án
Xem đáp án
Ta có
Hàm số liên tục tại x=0 thì
Câu 26:
Cho hàm số m là tham số
Tìm m để hàm số liên tục tại x=0
 Xem đáp án
Xem đáp án
Ta có
Để hàm số liên tục tại x=0 thì
Câu 28:
Cho hàm số . Giá trị của m để f(x) liên tục trên là
 Xem đáp án
Xem đáp án
Ta có và nên hàm số liên tục tại x=9
Ta cũng có và
Vậy để hàm số liên tục trên thì
Câu 29:
 Xem đáp án
Xem đáp án
Ta có
Để hàm số liên tục trên R thìCâu 30:
 Xem đáp án
Xem đáp án
Ta có . Để hàm số liên tục tại x=3 thì
Câu 31:
Cho hàm số. Giá trị của a để hàm số liên tục tại là
 Xem đáp án
Xem đáp án
Ta có
Để hàm số liên tục tại x=1 thì
Câu 32:
 Xem đáp án
Xem đáp án
Ta có
Để hàm số liên tục tại x=1 thì
Câu 33:
 Xem đáp án
Xem đáp án
Xét hàm số f(x) trên đoạn , khi đó
Ta có
Hàm số rõ ràng liên tục trên các khoảng và
Ta xét tại
Như vậy nên hàm số f(x) liên tục tại điểm
Ta xét tại
Vì nên hàm số f(x) gián đoạn tại điểm
Do đó, trên đoạn hàm số chỉ gián đoạn tại điểm .
Do tính chất tuần hoàn của hàm số và suy ra hàm số gián đoạn tại các điểm
Ta có
Vì nên . Vậy hàm số f có 321 điểm gián đoạn trên khoảng
