33 câu hỏi trắc nghiệm thuộc Dạng 2: Dãy số có giới hạn hữu hạn có đáp án

Câu 1:

Chứng minh rằng $\lim \frac{n^{2} + n}{n^{2} + 1} = 1.$

Hướng dẫn giải

Đặt $u_{n} = \frac{n^{2} + n}{n^{2} + 1}$ , ta có thể nhận xét $\lim (u_{n} - 1) = \lim (\frac{n^{2} + n}{n^{2} + 1} - 1) = \lim (\frac{n - 1}{n^{2} + 1}) = 0.$

Do đó $\lim u_{n} = 1$ . Ta được điều phải chứng minh.

Câu 2:

Chứng minh rằng

\lim \frac{3 n - 1}{2 n + 1} = \frac{3}{2} .

Xem đáp án

Hướng dẫn giải

Đặt $u_{n} = \frac{3 n - 1}{2 n + 1},$ ta có nhận xét:

$\lim (u_{n} - \frac{3}{2}) = \lim (\frac{3 n - 1}{2 n + 1} - \frac{3}{2}) = \lim \frac{- 5}{2 n + 1} = 0.$

Do đó

\lim u_{n} = \frac{3}{2} .

Ta được điều phải chứng minh.

Câu 3:

Chứng minh các giới hạn sau:

a) $\lim (\frac{- n^{3}}{n^{3} + 1}) = - 1.$

Xem đáp án

hướng dẫn giải

a) Ta có $\lim (\frac{- n^{3}}{n^{3} + 1} - (- 1)) = \lim \frac{1}{n^{3} + 1} .$

xét dãy $u_{n} = \frac{1}{n^{3} + 1} \Rightarrow |u_{n}| = \frac{1}{n^{3} + 1} < \frac{1}{n^{3}} = v_{n}, \forall n$ và $\lim v_{n} = \lim \frac{1}{n^{3}} = 0$

nên $\lim \frac{1}{n^{3} + 1} = 0.$

Do đó $\lim (\frac{- n^{3}}{n^{3} + 1}) = - 1.$

Ta được điều phải chứng minh.

Câu 4:

Chứng minh các giới hạn sau:

b, $\lim (\frac{n^{2} + 3 n + 2}{2 n^{2} + n}) = \frac{1}{2} .$

Xem đáp án

b) Ta có $\lim (\frac{n^{2} + 3 n + 2}{2 n^{2} + n} - \frac{1}{2}) = \lim \frac{5 n + 4}{2 (2 n^{2} + n)} .$

Xét dãy $u_{n} = \frac{5 n + 4}{2 (2 n^{2} + n)}$

$\Rightarrow |u_{n}| = \frac{5 n + 4}{2 (2 n^{2} + n)} < \frac{5 n + 4}{4 n^{2}} = \frac{5}{4 n} + \frac{1}{n^{2}} = v_{n}, \forall n .$

Mà $\lim v_{n} = \lim \frac{5}{4 n} + \lim \frac{1}{n^{2}} = 0$ nên $\lim \frac{3}{2 (3 n^{2} + n)} = 0.$

Do đó $\lim (\frac{n^{2} + 3 n + 2}{2 n^{2} + n}) = \frac{1}{2} .$

Ta được điều phải chứng minh.

Câu 5:

Chứng minh có giới hạn: $\lim (\frac{{3.3}^{n} - \sin 3 n}{3^{n}}) = 3.$

Xem đáp án

Hướng dẫn giải

Ta có $\lim (\frac{{3.3}^{n} - \sin 3 n}{3^{n}} - 3) = \lim (\frac{- \sin 3 n}{3^{n}}) .$

Ta lại có $\frac{|\sin 3 n|}{3^{n}} \leq \frac{1}{3^{n}} = {(\frac{1}{3})}^{n} \forall n$ và $\lim {(\frac{1}{3})}^{n} = 0$ , nên $\lim (\frac{- \sin 3 n}{3^{n}}) = 0.$

Do đó $\lim (\frac{{3.3}^{n} - \sin 3 n}{3^{n}}) = 3.$ Ta được điều cần phải chứng minh.

Câu 6:

Tìm các giới hạn sau:

a, $\lim \frac{- 4 n^{2} + n + 2}{2 n^{2} + n + 1} .$

Xem đáp án

hướng dẫn giải

a) $\lim \frac{- 4 n^{2} + n + 2}{2 n^{2} + n + 1} = \lim \frac{n^{2} (- 4 + \frac{1}{n} + \frac{2}{n^{2}})}{n^{2} (2 + \frac{1}{n} + \frac{1}{n^{2}})}$

$= \lim \frac{- 4 + \frac{1}{n} + \frac{2}{n^{2}}}{2 + \frac{1}{n} + \frac{1}{n^{2}}} .$

Mà

$\lim (2 + \frac{1}{n} + \frac{1}{n^{2}})$

. $= \lim 2 + l i m \frac{1}{n} + \lim \frac{1}{n^{2}} = 2 + 0 + 0 = 2 \neq 0$

$\begin{array}{l} \lim (- 4 + \frac{1}{n} + \frac{2}{n^{2}}) = \lim (- 4) + \lim \frac{1}{n} + \lim \frac{2}{n^{2}} \\ = - 4 + 0 + 0 = - 4 \end{array}$

Nên $\lim \frac{- 4 n^{2} + n + 2}{2 n^{2} + n + 1} = \frac{- 4}{2} = - 2.$

Chú ý: Như vậy, để tính các giới hạn trên chúng ta đã thực hiện phép chia cả tử và mẫu cho bậc cao nhất của n và sử dụng kết quả $\lim \frac{a}{n^{k}} = 0$ với k>0

Câu 7:

Tìm các giới hạn sau: b, $\lim {(2 n + 1)}^{2} (\frac{3}{n^{2} + 2 n} - \frac{1}{n^{2} + 3 n - 1}) .$

Xem đáp án

b) $\lim {(2 n + 1)}^{2} (\frac{3}{n^{2} + 2 n} - \frac{1}{n^{2} + 3 n - 1})$

$= \lim \frac{3 {(2 n + 1)}^{2}}{n^{2} + 2 n} - \lim \frac{{(2 n + 1)}^{2}}{n^{2} + 3 n - 1} .$

Mà

$\lim \frac{3 {(2 n + 1)}^{2}}{n^{2} + 2 n} = \lim \frac{3 {(2 + \frac{1}{n})}^{2}}{1 + \frac{2}{n}} = \frac{{3.2}^{2}}{1} = 12.$

$\lim \frac{{(2 n + 1)}^{2}}{n^{2} + 3 n - 1} = \frac{{(2 + \frac{1}{n})}^{2}}{1 + \frac{3}{n} - \frac{1}{n^{2}}} = \frac{2^{2}}{1} = 4.$

Nên

$\lim {(2 n + 1)}^{2} (\frac{3}{n^{2} + 2 n} - \frac{1}{n^{2} + 3 n - 1}) = 12 - 4 = 8.$

Chú ý: Như vậy, để tính các giới hạn trên chúng ta đã thực hiện phép tách thành các giới hạn nhỏ.

Câu 8:

Tìm các giới hạn sau:

a) $\lim \frac{\sqrt{9 n^{2} + 2 n} - 3 n}{4 n + 3} .$

Xem đáp án

a, $\lim \frac{\sqrt{9 n^{2} + 2 n} - 3 n}{4 n + 3} = \lim \frac{n \sqrt{9 + \frac{2}{n^{2}}} - 3 n}{4 n + 3} = \lim \frac{\sqrt{9 + \frac{2}{n^{2}}} - 3}{4 + \frac{3}{n}} = \frac{\sqrt{9 + 0} - 3}{4 + 0} = \frac{0}{4} = 0.$

Câu 9:

Tìm các giới hạn sau: b, $\lim \frac{3 \sqrt[4]{n^{5}} + 4 n - 2}{2 \sqrt[4]{n^{5}} - 3 n} .$

Xem đáp án

b, $\lim \frac{3 \sqrt[4]{n^{5}} + 4 n - 2}{2 \sqrt[4]{n^{5}} - 3 n} = \lim \frac{3 + \frac{4}{\sqrt[4]{n}} - \frac{2}{\sqrt[4]{n^{5}}}}{2 - \frac{3}{\sqrt[4]{n}}} = \frac{3 + 0 - 0}{2 - 0} = \frac{3}{2} .$

Câu 10:

Tìm các giới hạn sau:

a) $\lim (\sqrt{4 n^{2} + 2 n} - 2 n) .$

Xem đáp án

a) $\lim (\sqrt{4 n^{2} + 2 n} - 2 n) = \lim \frac{4 n^{2} + 2 n - 4 n^{2}}{\sqrt{4 n^{2} + 2 n} + 2 n} = \lim \frac{2 n}{2 n (\sqrt{1 + \frac{1}{2 n}} + 1)}$

= \lim \frac{1}{\sqrt{1 + \frac{1}{2 n}} + 1} = \frac{1}{\sqrt{1 + 0} + 1} = \frac{1}{2} .

Câu 11:

Tìm các giới hạn sau:

b,

\lim (\sqrt{n^{2} + 2 n + 3} - \sqrt[3]{n^{2} + n^{3}}) .

Xem đáp án

b) $\lim (\sqrt{n^{2} + 2 n + 3} - \sqrt[3]{n^{2} + n^{3}}) = \lim (\sqrt{n^{2} + 2 n + 3} - n) + \lim (n - \sqrt[3]{n^{2} + n^{3}}) .$

Mà

$\lim (\sqrt{n^{2} + 2 n + 3} - n) = \lim \frac{n^{2} + 2 n + 3 - n^{2}}{\sqrt{n^{2} + 2 n + 3} + n} = \lim \frac{2 + \frac{3}{n}}{\sqrt{1 + \frac{2}{n} + \frac{3}{n^{2}}} + 1} = \frac{2}{1 + 1} = 1.$

$\lim (n - \sqrt[3]{n^{2} + n^{3}}) = \lim \frac{n^{3} - (n^{2} + n^{3})}{n^{2} + n . \sqrt[3]{n^{2} + n^{3}} + {(\sqrt[3]{n^{2} + n^{3}})}^{2}}$

$= \lim \frac{- 1}{1 + \sqrt[3]{\frac{1}{n} + 1} + {(\sqrt[3]{\frac{1}{n} + 1})}^{2}} = \frac{- 1}{1 + 1 + 1} = - \frac{1}{3} .$

Vậy $\lim (\sqrt{n^{2} + 2 n + 3} - \sqrt[3]{n^{2} + n^{3}}) = 1 - \frac{1}{3} = \frac{2}{3} .$

Câu 12:

Tìm các giới hạn sau:

a)

\lim \frac{3^{n} - {2.5}^{n}}{7 + {3.5}^{n}} .

Xem đáp án

a) $\lim \frac{3^{n} - {2.5}^{n}}{7 + {3.5}^{n}} = \lim \frac{{(\frac{3}{5})}^{n} - 2}{7. {(\frac{1}{5})}^{n} + 3} = \frac{0 - 2}{7.0 + 3} = - \frac{2}{3}$

Câu 13:

Tìm các giới hạn sau: b,

\lim \frac{1 + 2 + 2^{2} + ... + 2^{n}}{1 + 3 + 3^{2} + ... + 3^{n}} .

Xem đáp án

b, $\lim \frac{1 + 2 + 2^{2} + ... + 2^{n}}{1 + 3 + 3^{2} + ... + 3^{n}} = \lim \frac{2^{n + 1} - 1}{\frac{3^{n + 1} - 1}{2}} = \lim 2. \frac{{(\frac{2}{3})}^{n + 1} - {(\frac{1}{3})}^{n + 1}}{1 - {(\frac{1}{3})}^{n + 1}} = 0.$

Câu 14:

Tìm các giới hạn sau:

a) $\lim (\frac{1}{1.3} + \frac{1}{3.5} + ... + \frac{1}{(2 n - 1) (2 n + 1)}) .$

Xem đáp án

a) Do $\frac{1}{(2 k - 1) (2 k + 1)} = \frac{1}{2} . \frac{2 k + 1 - (2 k - 1)}{(2 k - 1) (2 k + 1)} = \frac{1}{2} (\frac{1}{2 k - 1} - \frac{1}{2 k + 1})$

Suy ra $\lim (\frac{1}{1.3} + \frac{1}{3.5} + ... + \frac{1}{(2 k - 1) (2 k + 1)})$

$= \lim \frac{1}{2} (\frac{1}{1} - \frac{1}{3} + \frac{1}{3} - \frac{1}{5} + ... + \frac{1}{2 n - 1} - \frac{1}{2 n + 1}) = \lim \frac{1}{2} (1 - \frac{1}{2 n + 1}) = \frac{1}{2} .$

Câu 15:

Tìm các giới hạn sau: b, $\lim (1 - \frac{1}{2^{2}}) (1 - \frac{1}{3^{2}}) ... (1 - \frac{1}{n^{2}}) .$

Xem đáp án

b) Ta có $(1 - \frac{1}{2^{2}}) (1 - \frac{1}{3^{2}}) (1 - \frac{1}{4^{2}}) ... (1 - \frac{1}{{(n - 1)}^{2}}) (1 - \frac{1}{n^{2}})$

$= \frac{1}{2} . \frac{3}{2} . \frac{2}{3} . \frac{4}{3} . \frac{3}{4} . \frac{5}{4} ... \frac{n - 2}{n - 1} . \frac{n}{n - 1} . \frac{n - 1}{n} . \frac{n + 1}{n} = \frac{n + 1}{2 n} .$

Suy ra $\lim (1 - \frac{1}{2^{2}}) (1 - \frac{1}{3^{2}}) ... (1 - \frac{1}{n^{2}}) = \lim \frac{n + 1}{2 n} = \lim \frac{1 + \frac{1}{n}}{2} = \frac{1}{2} .$

Câu 16:

Tính các tổng sau:

a) $S = \frac{1}{3} + \frac{1}{3^{2}} + ... + \frac{1}{3^{n}} + ...$

Xem đáp án

a) Xét dãy số $(u_{n}) : \frac{1}{3}, \frac{1}{3^{2}}, ..., \frac{1}{3^{n}}, ...$ là một cấp số nhân có $u_{1} = \frac{1}{3}, q = \frac{1}{3} .$

Suy ra $S = \frac{1}{3} + \frac{1}{3^{2}} + ... + \frac{1}{3^{n}} = \frac{1 - {(\frac{1}{3})}^{n + 1}}{1 - \frac{1}{3}} - 1.$

Vậy $\lim S = \frac{1}{2} .$

Câu 17:

Tính các tổng sau: b, $S = 16 - 8 + 4 - 2 + ...$

Xem đáp án

b) Xét dãy số $(u_{n}) : 16; - 8; 4; - 2; ...$ là một cấp số nhân có $u_{1} = 16, q = - \frac{1}{2} .$

Suy ra

S = 16 - 8 + 4 - 2 + ...

có

\lim S = \frac{16}{1 + \frac{1}{2}} = \frac{32}{3} .

Câu 18:

Hãy biểu diễn các số thập phân vô hạn tuần hoàn sau dưới dạng phân số: a,

α = 0, 353535...

Xem đáp án

a)

α = 0, 353535... = 0, 35 + 0, 0035 + ... = \frac{35}{10^{2}} + \frac{35}{10^{4}} + ... = \frac{\frac{35}{10^{2}}}{1 - \frac{1}{10^{2}}} = \frac{35}{99} .

Câu 19:

Hãy biểu diễn các số thập phân vô hạn tuần hoàn sau dưới dạng phân số: b,

β = 5, 231231...

Xem đáp án

b) $β = 5, 231231... = 5 + 0, 231 + 0, 000231 + ... = 5 + \frac{231}{10^{3}} + \frac{231}{10^{6}} + ...$

$= 5 + \frac{\frac{231}{10^{3}}}{1 - \frac{1}{10^{3}}} = 5 + \frac{231}{999} = \frac{1742}{333} .$

Câu 20:

Tính giới hạn sau: $\lim \frac{n^{2} + 4 n}{n^{2} + 4 n + 5} .$

Xem đáp án

Hướng dẫn giải

Nhập vào máy tính biểu thức sau:

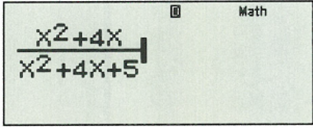
Tính giới hạn sau: a, lim n^2 +4n / n^2 +4n +5 (ảnh 1)

Sau đó bấm CALC.

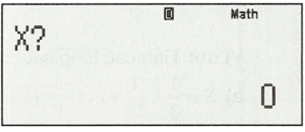
Tính giới hạn sau: a, lim n^2 +4n / n^2 +4n +5 (ảnh 2)

Nhập $x = 9999999999$ , sau đó bấm “=”, ta được kết quả:

Tính giới hạn sau: a, lim n^2 +4n / n^2 +4n +5 (ảnh 3)

Kết quả: Vậy giới hạn của dãy số bằng 1.

Câu 21:

Tính giới hạn sau $\lim (\sqrt{4 n^{2} - 5 n} - 2 n) .$

Xem đáp án

Hướng dẫn giải

Nhập vào máy tính biểu thức sau:

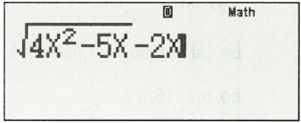
Tính giới hạn sau lim ( căn 4n^2 -5n -2n) (ảnh 1)

Sau đó bấm CACL.

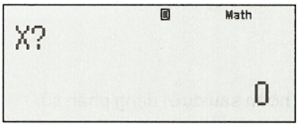
Tính giới hạn sau lim ( căn 4n^2 -5n -2n) (ảnh 2)

Nhập: $x = 9999999999$ , sau đó bấm “=”, ta được kết quả:

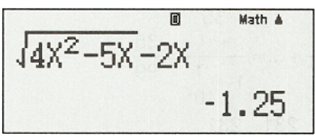
Tính giới hạn sau lim ( căn 4n^2 -5n -2n) (ảnh 3)

Kết quả: Vậy giới hạn của dãy số bằng $- 1, 25 = - \frac{5}{4} .$

Câu 22:

Giới hạn $\lim \frac{2 n + 1}{n + 2}$ bằng

A. 2

B. $\frac{3}{2}$

C. $\frac{- 1}{2}$

D. $\frac{1}{2}$

Xem đáp án

Ta có $\lim \frac{2 n + 1}{n + 2} = \lim \frac{2 + \frac{1}{n}}{1 + \frac{2}{n}} = \frac{2}{1} = 2.$

Chọn đáp án A

Câu 23:

Giới hạn $\lim \frac{n + 1}{n^{2} + 2}$ bằng

A. 2

B. $\frac{1}{2}$

C. 0

D. $\frac{1}{6}$

Xem đáp án

Chọn đáp án C

Ta có $\lim \frac{n + 1}{n^{2} + 2} = \lim \frac{\frac{1}{n} + \frac{1}{n^{2}}}{1 + \frac{2}{n^{2}}} = \frac{0}{1} = 0.$

Câu 24:

Giới hạn $\lim \frac{\sqrt{n^{2} + 1}}{2 n + 3}$ bằng

A. 0

B. $\frac{1}{2}$

C. $\frac{\sqrt{2}}{3} .$

D. $\frac{\sqrt{2}}{5} .$

Xem đáp án

Ta có $\lim \frac{\sqrt{n^{2} + 1}}{2 n + 3} = \lim \frac{\sqrt{1 + \frac{1}{n^{2}}}}{2 + \frac{3}{n}} = \frac{\sqrt{1}}{2} = \frac{1}{2} .$

Chọn đáp án B

Câu 25:

Giới hạn $\lim \frac{n^{2} + \sqrt[3]{n^{3} + 1} + n \sqrt{n}}{n \sqrt{n^{2} + 1} + 3}$ bằng

A. $\frac{1}{2}$

B. $\frac{1}{3}$

C. $\frac{2}{3}$

D. 1

Xem đáp án

Ta có

\lim \frac{n^{2} + \sqrt[3]{n^{3} + 1} + n \sqrt{n}}{n \sqrt{n^{2} + 1} + 3} = \lim \frac{1 + \sqrt[3]{\frac{1}{n^{3}} + \frac{1}{n^{6}}} + \sqrt{\frac{1}{n}}}{\sqrt{1 + \frac{1}{n^{2}}} + \frac{3}{n^{2}}} = \frac{1}{\sqrt{1}} = 1.

Chọn đáp án D

Câu 26:

Giới hạn $(\sqrt{9 n^{2} + 2 n} - \sqrt[3]{8 n^{3} + 6 n + 1} - n)$ là

A. $- \frac{1}{6} .$

B. $\frac{1}{6} .$

C. $\frac{1}{3} .$

D. $\frac{- 1}{3} .$

Xem đáp án

Ta có $\lim (\sqrt{9 n^{2} + 2 n} - \sqrt[3]{8 n^{3} + 6 n + 1} - n) = \lim (\sqrt{9 n^{2} + 2 n} - 3 n) - \lim (\sqrt[3]{8 n^{3} + 6 n + 1} - 2 n) = \frac{1}{3} - 0 = \frac{1}{3} .$

Chọn đáp án C

Câu 27:

Giới hạn $\lim \frac{{(n - \sqrt{n^{2} - 1})}^{2} + {(n + \sqrt{n^{2} - 1})}^{5}}{n^{5}}$ bằng

A. 64

B. 32

C. 16

D. 128

Xem đáp án

Chọn đáp án B

Ta có

\lim \frac{{(n - \sqrt{n^{2} - 1})}^{5} + {(n + \sqrt{n^{2} - 1})}^{5}}{n^{5}} = \lim \frac{{(1 - \sqrt{1 - \frac{1}{n^{2}}})}^{5} + {(1 + \sqrt{1 - \frac{1}{n^{2}}})}^{5}}{1} = 2^{5} = 32.

Câu 28:

Giới hạn $\lim \frac{1 - 4^{n}}{1 + 4^{n}}$ là

A. 1

B. -1

C. 0

D. $\frac{- 1}{3}$

Xem đáp án

Ta có

\lim \frac{1 - 4^{n}}{1 + 4^{n}} = \lim \frac{{(\frac{1}{4})}^{n} - 1}{{(\frac{1}{4})}^{n} + 1} = \frac{- 1}{1} = - 1.

Chọn đáp án B

Câu 29:

Giới hạn $\lim \frac{{4.3}^{n} + 7^{n + 1}}{{2.5}^{n} + 7^{n}}$ là

A. 4

B. 2

C. 7

D. -6

Xem đáp án

Ta có: $\lim \frac{{4.3}^{n} + 7^{n + 1}}{{2.5}^{n} + 7^{n}} = \lim \frac{4. {(\frac{3}{7})}^{n} + 7}{2. {(\frac{5}{7})}^{n} + 1} = \frac{7}{1} = 7.$

Chọn đáp án C

Câu 30:

Giới hạn

\lim (\frac{1}{2.4} + \frac{1}{4.6} + ... + \frac{1}{2 n (2 n + 2)})

bằng

A. $\frac{1}{3}$

B. $\frac{- 1}{2}$

C. 2

D. $\frac{1}{4}$

Xem đáp án

Ta có

\lim (\frac{1}{2.4} + \frac{1}{4.6} + ... + \frac{1}{2 n (2 n + 2)}) = \lim \frac{1}{2} (\frac{1}{2} - \frac{1}{4} + \frac{1}{4} - \frac{1}{6} + ... + \frac{1}{2 n} - \frac{1}{2 n + 3}) = \lim \frac{1}{2} (\frac{1}{2} - \frac{1}{2 n + 2}) = \frac{1}{4} .

Chọn đáp án D

Câu 31:

Giới hạn $\lim [\frac{1}{1 \sqrt{2} + 2 \sqrt{1}} + \frac{1}{2 \sqrt{3} + 3 \sqrt{2}} + ... + \frac{1}{n \sqrt{n + 1} + (n + 1) \sqrt{n}}]$ là

A. -2

B. 1

C. $\frac{3}{2}$

D. $\frac{- 5}{2}$

Xem đáp án

Ta có $\frac{1}{k \sqrt{k + 1} + (k + 1) \sqrt{k}} = \frac{k \sqrt{k + 1} - (k + 1) \sqrt{k}}{- k (k + 1)} = \frac{1}{\sqrt{k}} - \frac{1}{\sqrt{k + 1}} .$

Suy ra $u_{n} = \frac{1}{\sqrt{1}} - \frac{1}{\sqrt{n + 1}} \Rightarrow \lim u_{n} = 1.$

Chọn đáp án B

Câu 32:

Tổng $S = 8 + 88 + 888 + ... + \underset{n c h ö õ s o á 8}{\underset{⏟}{888...8}}$ bằng

A. $10^{n + 1} - 10 - 36 n .$

B. $10^{n + 1} + 10 + 54 n .$

C. $\frac{8}{81} (10^{n + 1} - 10 - 9 n)$

D. $\frac{1}{81} (10^{n + 1} - 10 - 72 n) .$

Xem đáp án

Chọn đáp án C

Ta viết lại $S = \frac{8}{9} (9 + 99 + 999 + ... + \underset{n s o á 9}{\underset{⏟}{99...9}}) = \frac{8}{9} (10 - 1 + 100 - 1 + ... + \underset{n s o á 0}{\underset{⏟}{100..0}} - 1)$

$\Rightarrow S = \frac{8}{9} [(10 + 100 + ... + \underset{n s o á 0}{\underset{⏟}{100..00}}) - n] \Leftrightarrow S = \frac{8}{9} [\frac{10. (10^{n} - 1)}{10 - 1} - n] = \frac{8}{9} (\frac{10^{n + 1} - 10}{9} - n) = \frac{8}{81} (10^{n + 1} - 10 - 9 n) .$

Câu 33:

Tổng $S = 5 - \sqrt{5} + 1 - \frac{1}{\sqrt{5}} + \frac{1}{5} - ...$ bằng

A. $\frac{25 - 5 \sqrt{5}}{4} .$

B. $\frac{25 - 5 \sqrt{3}}{4} .$

C. $\frac{25 + 3 \sqrt{5}}{4} .$

D. $\frac{5 + 3 \sqrt{5}}{4} .$

Xem đáp án

Ta có

S = 5 - \sqrt{5} + 1 - \frac{1}{\sqrt{5}} + \frac{1}{5} - ... = \frac{5}{1 + \frac{1}{\sqrt{5}}} = \frac{5 \sqrt{5}}{1 + \sqrt{5}} = \frac{25 - 5 \sqrt{5}}{4} .

chọn đáp án A

Bài tập chuyên đề Toán 11 Bài 1: Giới hạn của dãy số có đáp án

Dạng 2: Dãy số có giới hạn hữu hạn có đáp án

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương