Giải SGK Toán 7 (Chân trời sáng tạo): Bài tập cuối chương 8

Giải SGK Toán 7: Bài tập cuối chương 8

Giải Toán 7 trang 84 Tập 2

Bài 1 trang 84 Toán 7 Tập 2:

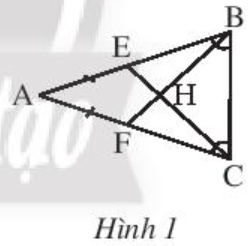
Cho tam giác ABC cân tại A ($\widehat{A}<90°$). Hai đường cao BE và CF cắt nhau tại H.

a) Chứng minh rằng ∆BEC = ∆CFB.

b) Chứng minh rằng ∆AHF = ∆AHE.

c) Gọi I là trung điểm của BC. Chứng minh rằng ba điểm A, H, I thẳng hàng.

Lời giải:

GT	$∆$ABC cân tại A, $\widehat{A}<90°$; Hai đường cao BE và CF cắt nhau tại H; c) I là trung điểm của BC.
KL	a) ∆BEC = ∆CFB. b) ∆AHF = ∆AHE. c) Ba điểm A, H, I thẳng hàng.

 

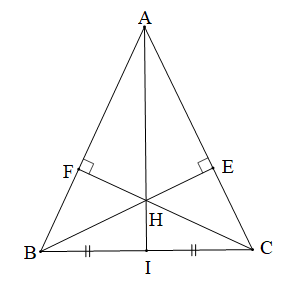
a) Tam giác ABC cân tại A (giả thiết) nên $\widehat{ABC}=\widehat{ACB}$ và AB = AC.

Xét ∆BEC (vuông tại E) và ∆CFB (vuông tại F) có:

$\widehat{ECB}=\widehat{FBC}$ (do $\widehat{ABC}=\widehat{ACB}$);

BC là cạnh chung.

Do đó ∆BEC = ∆CFB (cạnh huyền - góc nhọn).

Vậy ∆BEC = ∆CFB.

b) Vì ∆BEC = ∆CFB (chứng minh câu a)

Suy ra EC = FB (hai cạnh tương ứng).

Mà AB = AC (chứng minh câu a) nên AB - FB = AC - EC hay AF = AE.

Xét ∆AHF (vuông tại F) và ∆AHE (vuông tại E) có:

AF = AE (chứng minh trên);

AH là cạnh chung.

Do đó ∆AHF = ∆AHE (cạnh huyền - cạnh góc vuông).

Vậy ∆AHF = ∆AHE.

c) Vì ∆AHF = ∆AHE (chứng minh câu b)

Suy ra $\widehat{HAF}=\widehat{HAE}$ (hai góc tương ứng).

Do đó AH là tia phân giác của $\widehat{BAC}$  (1).

Xét $∆$ABI và $∆$ACI có:

AB = AC (chứng minh câu a);

AI là cạnh chung;

IB = IC (do I là trung điểm của BC).

Do đó ∆ABI = ∆ACI (c.c.c)

Suy ra $\widehat{BAI}=\widehat{CAI}$ (hai góc tương ứng)

Do đó AI là tia phân giác của $\widehat{BAC}$  (2)

Từ (1) và (2) suy ra AH trùng AI hay A, H, I thẳng hàng.

Bài 2 trang 84 Toán 7 Tập 2:

Cho tam giác ABC vuông tại A, vẽ đường cao AH. Trên tia đối của tia HA lấy điểm M sao cho H là trung điểm của AM.

a) Chứng minh rằng tam giác ABM cân.

b) Chứng minh rằng ∆ABC = ∆MBC.

Lời giải:

GT	$∆$ABC vuông tại A, đường cao AH, M thuộc tia đối của tia HA, H là trung điểm của AM.
KL	a) ∆ABM cân. b) ∆ABC = ∆MBC.

 

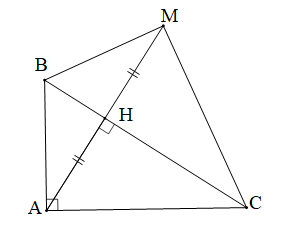
a) Ta có AH ⊥ BC tại H (giả thiết) do đó BC ⊥ AM tại H

Mà H là trung điểm của AM (giả thiết)

Suy ra BC là đường trung trực của AM.

Suy ra BA = BM (tính chất đường trung trực)

Do đó tam giác ABM cân tại B.

Vậy tam giác ABM cân tại B.

b) Vì BC là đường trung trực của đoạn thẳng AM (chứng minh câu a)

Nên CA = CM (tính chất đường trung trực)

Xét ∆ABC và ∆MBC có:

BA = BM (chứng minh câu a),

CA = CM (chứng minh trên)

BC là cạnh chung.

Do đó ∆ABC = ∆MBC (c.c.c)

Vậy ∆ABC = ∆MBC.

Bài 3 trang 84 Toán 7 Tập 2:

Cho tam giác ABC vuông tại A (AB < AC), vẽ đường cao AH. Trên tia đối của tia HC lấy điểm D sao cho HD = HC.

a) Chứng minh rằng AC = AD.

b) Chứng minh rằng $\widehat{A\text{D}B}=\widehat{BAH}$.

Lời giải:

GT	$∆$ABC vuông tại A, AB < AC, đường cao AH, H ∈ tia đối của tia HC, HD = HC
KL	a) AC = AD. b) $\widehat{A\text{D}B}=\widehat{BAH}$.

 

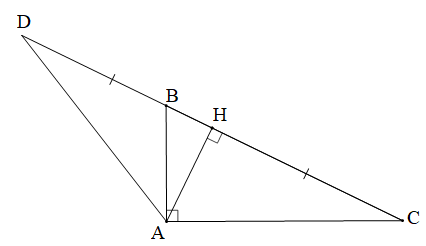
a) Vì H thuộc tia đối của tia HC sao cho HD = HC (giả thiết) nên H là trung điểm của CD.

Ta có: AH ⊥ CD tại trung điểm H của CD

Nên AH là đường trung trực của đoạn thẳng CD.

Suy ra AC = AD (tính chất trung trực của một đoạn thẳng)

Vậy AC = AD.

b) Tam giác ACD có AC = AD (chứng minh câu a) nên tam giác ACD cân tại A.

Do đó $\widehat{A\text{D}B}=\widehat{ACB}$ (tính chất tam giác cân)

Xét ∆ABC vuông tại A có:

$\widehat{ACB}+\widehat{ABC}=90°$ (trong tam giác vuông, hai góc nhọn phụ nhau)

Suy ra $\widehat{ACB}=90°-\widehat{ABC}$  (1)

Xét ∆ABH vuông tại H có:

$\widehat{BAH}+\widehat{ABH}=90°$(trong tam giác vuông, hai góc nhọn phụ nhau)

Suy ra $\widehat{BAH}=90°-\widehat{ABH}$  (2)

Từ (1) và (2) suy ra $\widehat{ACB}=\widehat{BAH}$.

Mà $\widehat{ACB}=\widehat{A\text{D}B}$ (chứng minh trên) nên $\widehat{A\text{D}B}=\widehat{BAH}$.

Vậy $\widehat{A\text{D}B}=\widehat{BAH}$.

Bài 4 trang 84 Toán 7 Tập 2:

Cho tam giác ABC vuông tại A (AB < AC). Trên cạnh BC lấy điểm N sao cho BA = BN. Kẻ BE $\perp$ AN (E $\in$ AN).

a) Chứng minh BE là tia phân giác của góc ABN.

b) Kẻ đường cao AH của tam giác ABC. Gọi K là giao điểm của AH với BE. Chứng minh rằng NK // CA.

c) Đường thẳng BK cắt AC tại F. Gọi G là giao điểm của đường thẳng AB với NF. Chứng minh rằng tam giác GBC cân.

Lời giải:

GT	$∆$ABC vuông tại A, AB < AC, N ∈ BC, BA = BN, BE $\perp$ AN (E $\in$ AN). b) AH là đường cao, K là giao điểm của AH với BE. c) BK cắt AC tại F, G là giao điểm của AB với NF.
KL	a) BE là tia phân giác của góc ABN. b) NK // CA. c) $∆$GBC cân.

 

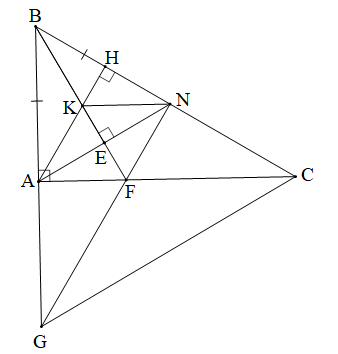
a) Xét ∆ABE (vuông tại E) và ∆NBE (vuông tại E) có:

BA = BN (giả thiết);

AE là cạnh chung.

Do đó ∆ABE = ∆NBE (cạnh huyền – cạnh góc vuông)

Suy ra $\widehat{ABE}=\widehat{NBE}$ (hai góc tương ứng)

Do đó BE là tia phân giác của góc ABN.

Vậy BE là tia phân giác của góc ABN.

b) Ta có ∆ABN có BE ⊥ AN, AH ⊥ BN (giả thiết)

Suy ra ∆ABN có hai đường cao AH và BE cắt nhau tại K.

Do đó K là trực tâm của tam giác ABN.

Suy ra NK $\perp$ AB.

Mà CA $\perp$ AB (do ∆ABC vuông tại A)

Do đó NK // AC.

Vậy NK // AC.

c) Vì BE là tia phân giác của $\widehat{ABN}$ (chứng minh câu a) nên $\widehat{ABF}=\widehat{NBF}$.

Xét ∆ABF và ∆NBF có:

BA = BN (giả thiết),

$\widehat{ABF}=\widehat{NBF}$ (chứng minh trên),

BF là cạnh chung

Do đó ∆ABF = ∆NBF (c.g.c)

Suy ra AF = NF (hai cạnh tương ứng) và $\widehat{BAF}=\widehat{BNF}=90°$ (hai góc tương ứng).

Do đó FN $\perp$ BC.

Xét ∆AFG (vuông tại A) và ∆NFC (vuông tại N) có:

AF = NF (chứng minh trên),

$\widehat{AFG}=\widehat{NFC}$ (hai góc đối đỉnh),

Do đó ∆AFG = ∆NFC (cạnh góc vuông – góc nhọn kề).

Suy ra AG = NC (hai cạnh tương ứng).

Lại có BA = BN (giả thiết)

Do đó BA + AG = BN + NC

Hay BG = BC.

Tam giác BGC có BG = BC nên tam giác BGC cân tại B.

Vậy tam giác BGC cân tại B.

Bài 5 trang 84 Toán 7 Tập 2:

Cho tam giác ABC nhọn (AB < AC), vẽ đường cao AH. Đường trung trực của cạnh BC cắt AC tại M, cắt BC tại N.

a) Chứng minh rằng $\widehat{BMN}=\widehat{HAC}$.

b) Kẻ MI ⊥ AH (I $\in$ AH), gọi K là giao điểm của AH với BM. Chứng minh rằng I là trung điểm của AK.

Lời giải:

GT	$∆$ABC nhọn, AB < AC, đường cao AH, MN là đường trung trực của BC, M $\in$ AC, N $\in$ BC, b) MI $\perp$ AH (I $\in$ AH), K là giao điểm của AH với BM
KL	a) $\widehat{BMN}=\widehat{HAC}$ b) I là trung điểm của AK.

 

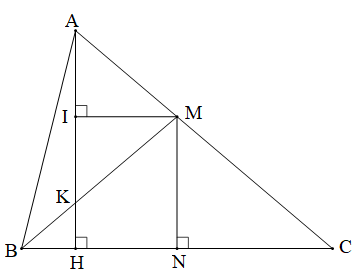
a) Vì M, N nằm trên đường trung trực của BC (giả thiết) nên MN là đường trung trực của BC

Suy ra MN ⊥ BC tại trung điểm N của BC và MB = MC (tính chất đường trung trực)

Xét ∆BMN (vuông tại N) và ∆CMN (vuông tại N) có:

MB = MC (chứng minh trên),

MN là cạnh chung.

Do đó ∆BMN = ∆CMN (cạnh huyền - cạnh góc vuông).

Suy ra $\widehat{BMN}=\widehat{CMN}$ (hai góc tương ứng) (1).

Mặt khác: MN $\perp$ BC (chứng minh trên),

AH $\perp$ BC (giả thiết)

Do đó MN // AH.

Suy ra $\widehat{CMN}=\widehat{CAH}$ (hai góc đồng vị) (2).

Từ (1) và (2) suy ra $\widehat{BMN}=\widehat{CAH}$.

Vậy $\widehat{BMN}=\widehat{HAC}$.

b) Ta có MN // AH (chứng minh câu a)

Suy ra $\widehat{BMN}=\widehat{AKM}$ (hai góc so le trong)

Mà $\widehat{BMN}=\widehat{HAC}$ (chứng minh câu a)

Suy ra $\widehat{AKM}=\widehat{HAC}$ hay $\widehat{AKM}=\widehat{KAM}$ 

Do đó tam giác AMK cân tại M

Suy ra MA = MB nên M nằm trên đường trung trực của AK.

Lại có MI ⊥ AK tại I nên MI là đường trung trực của AK.

Do đó I là trung điểm của AK.

Vậy I là trung điểm của AK.

Bài 6 trang 84 Toán 7 Tập 2:

Cho tam giác nhọn MNP. Các trung tuyến ME và NF cắt nhau tại G. Trên tia đối của tia FN lấy điểm D sao cho FD = FN.

a) Chứng minh rằng ∆MFN = ∆PFD.

b) Trên đoạn thẳng FD lấy điểm H sao cho F là trung điểm của GH. Gọi K là trung điểm của DP. Chứng minh rằng ba điểm M, H, K thẳng hàng.

Lời giải:

GT	$∆$MNP nhọn, trung tuyến ME và NF cắt nhau tại G, D thuộc tia đối của tia FN, FD = FN. b) H ∈ FD, F là trung điểm của GH, K là trung điểm của DP.
KL	a) ∆MFN = ∆PFD. b) Ba điểm M, H, K thẳng hàng.

 

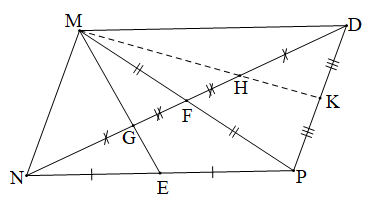
a) Xét ∆MFN và ∆PFD có:

MF = PF (do F là trung điểm của MP);

$\widehat{MFN}=\widehat{PF\text{D}}$ (hai góc đối đỉnh);

FN = FD (giả thiết).

Do đó ∆MFN = ∆PFD (c.g.c)

Vậy ∆MFN = ∆PFD.

b) Ta có: F là trung điểm của GH (giả thiết) nên FH = FG.

Mà FD = FN (giả thiết)

Do đó FD – FH = FN – FG hay DH = NG.

Mặt khác: tam giác MNP có hai trung tuyến ME và NF cắt nhau tại G (giả thiết)

Do đó G là trọng tâm tam giác MNP

Suy ra $NG=\frac{2}{3}NF$ (tính chất trọng tâm của tam giác)

Mà DH = NG (chứng minh trên) và NF = DF (giả thiết)

Do đó $DH=\frac{2}{3}DF$

Tam giác MDP có đường trung tuyến DF và DH = $\frac{2}{3}$DF nên H là trọng tâm của tam giác MDP.

Lại có K là trung điểm của DP (giả thiết) nên MK là đường trung tuyến của tam giác MDP

Do đó trung tuyến MK đi qua trọng tâm H

Suy ra M, H, K thẳng hàng.

Vậy M, H, K thẳng hàng.

Bài 7 trang 84 Toán 7 Tập 2:

Cho tam giác ABC vuông tại A có $AB=\frac{1}{2}AC$, AD là tia phân giác $\widehat{BAC}$ (D ∈ BC). Gọi E là trung điểm của AC.

a) Chứng minh rằng DE = DB.

b) AB cắt DE tại K. Chứng minh rằng tam giác DCK cân và B là trung điểm của đoạn thẳng AK.

c) AD cắt CK tại H. Chứng minh rằng AH ⊥ KC.

Lời giải:

GT	$∆$ABC vuông tại A, $AB=\frac{1}{2}AC$, AD là tia phân giác $\widehat{BAC}$ (D ∈ BC). E là trung điểm của AC. b) AB cắt DE tại K. c) AD cắt CK tại H.
KL	a) DE = DB. b) ∆DCK cân và B là trung điểm của đoạn thẳng AK. c) AH ⊥ KC.

 

a) Do E là trung điểm của AC (giả thiết) nên AE = $\frac{1}{2}$AC.

Mà AB = $\frac{1}{2}$AC (giả thiết) nên AE = AB.

Vì AD là tia phân giác của $\widehat{BAC}$ (giả thiết) nên $\widehat{BA\text{D}}=\widehat{E\text{A}D}$.

Xét ∆ABD và ∆AED có:

AB = AE (chứng minh trên);

$\widehat{BA\text{D}}=\widehat{E\text{A}D}$ (chứng minh trên);

AD là cạnh chung.

Do đó ∆ABD = ∆AED (c.g.c)

Suy ra DB = DE (hai cạnh tương ứng).

Vậy DE = DB.

b)

+) Vì ∆ABD = ∆AED (chứng minh câu a)

Suy ra $\widehat{ADB}=\widehat{ADE}$ (hai góc tương ứng).

Mà $\widehat{KDB}=\widehat{C\text{D}E}$ (hai góc đối đỉnh)

Do đó $\widehat{A\text{D}B}+\widehat{K\text{D}B}=\widehat{A\text{D}E}+\widehat{C\text{D}E}$ 

Hay $\widehat{ADK}=\widehat{A\text{D}C}$.

Xét ∆ADK và ∆ADC có:

$\widehat{DAK}=\widehat{DAC}$ (do AD là tia phân giác của góc BAC);

AD là cạnh chung;

$\widehat{ADK}=\widehat{A\text{D}C}$ (chứng minh trên)

Do đó ∆ADK = ∆ADC (g.c.g)

Suy ra DK = DC (hai cạnh tương ứng)

Do đó tam giác DCK cân tại D.

+) Vì ∆ADK = ∆ADC (chứng minh trên)

Suy ra AK = AC (hai cạnh tương ứng)

Mà $AB=\frac{1}{2}AC$ (giả thiết) nên $AB=\frac{1}{2}AK$ 

Mà A, B, K thẳng hàng nên B là trung điểm của AK.

Vậy B là trung điểm của AK.

c) Ta có AK = AC (chứng minh câu b) nên A nằm trên đường trung trực của KC.

Lại có DK = DC (chứng minh câu b) nên D nằm trên đường trung trực của KC.

Do đó AD là đường trung trực của KC

Suy ra AD ⊥ KC hay AH ⊥ KC

Vậy AH ⊥ KC.

Bài 8 trang 84 Toán 7 Tập 2:

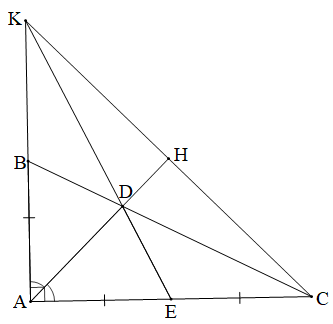
Ở Hình 1, cho biết AE = AF và $\widehat{ABC}=\widehat{ACB}$. Chứng minh rằng AH là đường trung trực của BC.

 

Lời giải:

GT	$∆$ABC, AE = AF, $\widehat{ABC}=\widehat{ACB}$.
KL	AH là đường trung trực của BC.

 

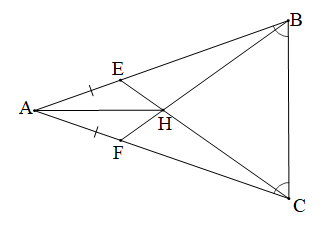
Tam giác ABC có $\widehat{ABC}=\widehat{ACB}$ (giả thiết) nên tam giác ABC cân tại A.

Do đó AB = AC.

Mà AE = AF (giả thiết)

Nên AB - AE = AC - AF

Hay BE = CF.

Xét ∆EBC và ∆FCB có:

BE = CF (chứng minh trên);

$\widehat{EBC}=\widehat{FCB}$ (do $\widehat{ABC}=\widehat{ACB}$);

BC là cạnh chung

Do đó ∆EBC = ∆FCB (c.g.c)

Suy ra $\widehat{ECB}=\widehat{FBC}$ (hai góc tương ứng)

Hay $\widehat{HCB}=\widehat{HBC}$.

Do đó tam giác HBC cân tại H.

Suy ra HB = HC, từ đó ta có H thuộc trung trực của BC.

Lại có AB = AC (chứng minh trên)

Suy ra A thuộc trung trực của BC

Do đó AH là đường trung trực của BC.

Vậy AH là đường trung trực của BC.

Bài 9 trang 84 Toán 7 Tập 2:

Cho tam giác ABC vuông tại A. Tia phân giác của góc C cắt AB ở M. Từ B kẻ BH vuông góc với đường thẳng CM (H ∈ CM). Trên tia đối của tia HC lấy điểm E sao cho HE = HM.

a) Chứng minh rằng tam giác MBE cân.

b) Chứng minh rằng $\widehat{EBH}=\widehat{ACM}$.

c) Chứng minh rằng EB ⊥ BC.

Lời giải:

GT	$∆$ABC vuông tại A, Tia phân giác của góc C cắt AB ở M, BH ⊥ CM (H ∈ CM). E thuộc tia đối của tia HC, HE = HM
KL	a) $∆$MBE cân. b) $\widehat{EBH}=\widehat{ACM}$ c) EB ⊥ BC.

 

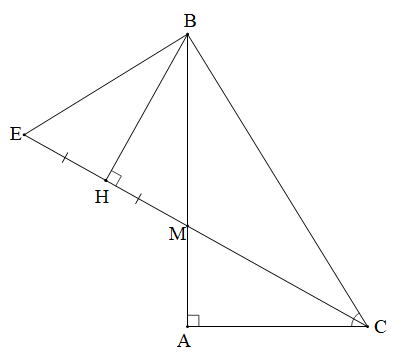
a) Vì E thuộc tia đối của tia HC và HE = HM (giả thiết) nên H là trung điểm của ME.

Mà BH ⊥ CM tại H (giả thiết)

Do đó BH là đường trung trực của EM

Suy ra BM = BE.

Tam giác MBE có BM = BE nên tam giác MBE cân tại B.

Vậy tam giác MBE cân tại B.

b)

+) Xét ∆BEH (vuông tại H) và ∆BMH (vuông tại H) có:

BH là cạnh chung,

BE = BM (chứng minh câu a)

Do đó ∆BEH = ∆BMH (cạnh huyền – cạnh góc vuông)

Suy ra $\widehat{HBE}=\widehat{HBM}$ (hai góc tương ứng) (1).

+) Xét ∆BHM vuông tại H có:

$\widehat{HBM}+\widehat{BMH}=90°$ (trong tam giác vuông, hai góc nhọn phụ nhau)

Suy ra $\widehat{HBM}=90°-\widehat{BMH}$  (2)

Xét ∆ACM vuông tại A có:

$\widehat{ACM}+\widehat{CMA}=90°$ (trong tam giác vuông, hai góc nhọn phụ nhau)

Suy ra $\widehat{ACM}=90°-\widehat{CMA}$  (3)

Mà $\widehat{BMH}=\widehat{CMA}$ (hai góc đối đỉnh) (4)

Từ (2), (3), (4) suy ra $\widehat{HBM}=\widehat{ACM}$  (5).

Từ (1) và (5) suy ra $\widehat{HBE}=\widehat{ACM}$.

Vậy $\widehat{EBH}=\widehat{ACM}$

c) Vì CM là tia phân giác của $\widehat{BCA}$ (giả thiết) nên $\widehat{ACM}=\frac{1}{2}\widehat{BCA}$  (6)

Lại có $\widehat{HBE}=\widehat{HBM}$ (chứng minh câu b)

Nên BH là tia phân giác của $\widehat{EBM}$ do đó $\widehat{EBH}=\frac{1}{2}\widehat{EBM}$  (7)

Mà $\widehat{EBH}=\widehat{ACM}$ (chứng minh câu b) (8)

Từ (6), (7) và (8) ta có $\widehat{BCA}=\widehat{EBM}$ 

Xét tam giác ACB vuông tại A có:

$\widehat{ABC}+\widehat{BCA}=90°$ (trong tam giác vuông, hai góc nhọn phụ nhau)

Do đó $\widehat{ABC}+\widehat{EBM}=90°$

Hay $\widehat{EBC}=90°$, từ đó ta có EB ⊥ BC.

Vậy EB ⊥ BC.

Bài 10 trang 84 Toán 7 Tập 2:

Trên đường thẳng a lấy ba điểm phân biệt I, J, K (J ở giữa I và K). Kẻ đường thẳng b vuông góc với a tại J, trên b lấy điểm M khác điểm J. Đường thẳng qua I vuông góc với MK cắt b tại N. Chứng minh rằng KN vuông góc với MI.

Lời giải

GT	I, J, K ∈ a (J ở giữa I và K), b ⊥ a tại J, M ∈ b, M ≠ J, IN ⊥ MK, N ∈ b
KL	KN ⊥ MI.

 

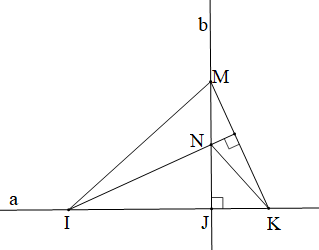
Nối IM.

Xét tam giác MIK có MJ ⊥ IK, IN ⊥ MK.

Mà MJ cắt IN tại N nên N là trực tâm của tam giác MIK.

Do đó NK ⊥ MI.

Vậy NK ⊥ MI.

Xem thêm lời giải bài tập SGK Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác: 

Bài 8: Tính chất ba đường cao của tam giác

Bài 9: Tính chất ba đường phân giác của tam giác

Bài 10: Hoạt động thực hành và trải nghiệm. Làm giàn hoa tam giác để trang trí lớp học

Bài 1: Làm quen với biến cố ngẫu nhiên

Bài 2: Làm quen với xác suất của biến cố ngẫu nhiên