Bài 1 trang 84 Toán 7 Tập 2:
Cho tam giác ABC cân tại A (). Hai đường cao BE và CF cắt nhau tại H.
a) Chứng minh rằng ∆BEC = ∆CFB.
b) Chứng minh rằng ∆AHF = ∆AHE.
c) Gọi I là trung điểm của BC. Chứng minh rằng ba điểm A, H, I thẳng hàng.
|
GT |
ABC cân tại A, ; Hai đường cao BE và CF cắt nhau tại H; c) I là trung điểm của BC. |
|
KL |
a) ∆BEC = ∆CFB. b) ∆AHF = ∆AHE. c) Ba điểm A, H, I thẳng hàng. |
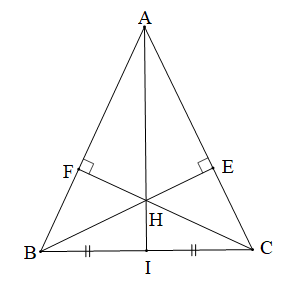
a) Tam giác ABC cân tại A (giả thiết) nên và AB = AC.
Xét ∆BEC (vuông tại E) và ∆CFB (vuông tại F) có:
(do );
BC là cạnh chung.
Do đó ∆BEC = ∆CFB (cạnh huyền - góc nhọn).
Vậy ∆BEC = ∆CFB.
b) Vì ∆BEC = ∆CFB (chứng minh câu a)
Suy ra EC = FB (hai cạnh tương ứng).
Mà AB = AC (chứng minh câu a) nên AB - FB = AC - EC hay AF = AE.
Xét ∆AHF (vuông tại F) và ∆AHE (vuông tại E) có:
AF = AE (chứng minh trên);
AH là cạnh chung.
Do đó ∆AHF = ∆AHE (cạnh huyền - cạnh góc vuông).
Vậy ∆AHF = ∆AHE.
c) Vì ∆AHF = ∆AHE (chứng minh câu b)
Suy ra (hai góc tương ứng).
Do đó AH là tia phân giác của (1).
Xét ABI và ACI có:
AB = AC (chứng minh câu a);
AI là cạnh chung;
IB = IC (do I là trung điểm của BC).
Do đó ∆ABI = ∆ACI (c.c.c)
Suy ra (hai góc tương ứng)
Do đó AI là tia phân giác của (2)
Từ (1) và (2) suy ra AH trùng AI hay A, H, I thẳng hàng.
Xem thêm lời giải bài tập Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác:
Bài 9: Tính chất ba đường phân giác của tam giác
Bài 10: Hoạt động thực hành và trải nghiệm. Làm giàn hoa tam giác để trang trí lớp học
Bài 1: Làm quen với biến cố ngẫu nhiên
Bài 2: Làm quen với xác suất của biến cố ngẫu nhiên
Bài 3: Hoạt động thực hành và trải nghiệm. Nhảy theo xúc xắc