Giải SGK Toán 7 Bài 4 (Cánh diều): Phép nhân đa thức một biến

A. Câu hỏi

Giải Toán 7 trang 60 Tập 2

Câu hỏi khởi động trang 60 Toán 7 Tập 2: Trong quá trình biến đổi và tính toán những biểu thức đại số, nhiều khi ta phải thực hiện phép nhân hai đa thức một biến, chẳng hạn ta cần thực hiện phép nhân sau:

(x – 1)(x² + x + 1).

Làm thế nào để thực hiện được phép nhân hai đa thức một biến?

Lời giải:

Sau bài học này chúng ta sẽ giải quyết được câu hỏi trên như sau:

Muốn nhân một đa thức với một đa thức, ta nhân mỗi đơn thức của đa thức này với từng đơn thức của đa thức kia rồi cộng các tích với nhau.

Hoạt động 1 trang 60 Toán 7 Tập 2: Thực hiện phép tính:

a) x² . x⁴;

b) 3x² . x³;

c) ax^m . bxⁿ (a ≠ 0; b ≠ 0; m, n ∈ ℕ).

Lời giải:

a) x² . x⁴ = x²⁺⁴ = x⁶.

Vậy x² . x⁴ = x⁶.

b) 3x² . x³ = 3x²⁺³ = 3x⁵.

Vậy 3x² . x³ = 3x⁵.

c) ax^m . bxⁿ = a . b . x^m . xⁿ = abx^m+n (a ≠ 0; b ≠ 0; m, n ∈ ℕ).

Vậy ax^m . bxⁿ = abx^m+n với a ≠ 0; b ≠ 0; m, n ∈ ℕ.

Luyện tập 1 trang 60 Toán 7 Tập 2: Tính:

a) 3x⁵ . 5x⁸;

b) -2x^m+2 . 4x^n-2 (m, n ∈ ℕ; n > 2).

Lời giải:

a) Ta có: 3x⁵ . 5x⁸ = 3 . 5 . x⁵ . x⁸ = 15 . x⁵⁺⁸ = 15x¹³.

Vậy 3x⁵ . 5x⁸ = 15x¹³.

b) Ta có:

-2x^m+2 . 4x^n-2 

= -2 . 4 . x^m+2 . x^n-2

= -8 . x^m+2+n-2

= -8x^m+n  (m, n ∈ ℕ; n > 2).

Vậy -2x^m+2 . 4x^n-2 = -8x^m+n  (m, n ∈ ℕ; n > 2).

Hoạt động 2 trang 60 Toán 7 Tập 2:

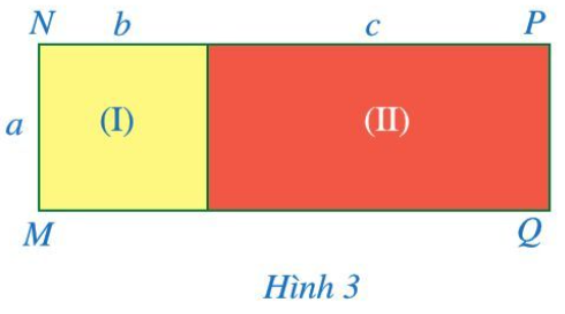
Quan sát hình chữ nhật MNPQ ở Hình 3.

a) Tính diện tích mỗi hình chữ nhật (I), (II);

b) Tính diện tích của hình chữ nhật MNPQ;

c) So sánh: a(b + c) và ab + ac.

Lời giải:

a) Diện tích hình chữ nhật (I) là ab (đơn vị diện tích).

Diện tích hình chữ nhật (II) là ac (đơn vị diện tích).

b) Quan sát Hình 3 ta thấy chiều dài của hình chữ nhật MNPQ là b + c.

Do đó diện tích hình chữ nhật MNPQ là a(b + c) (đơn vị diện tích).

c) Quan sát Hình 3 ta thấy hình chữ nhật MNPQ là hình được ghép bởi hình chữ nhật (I) và hình chữ nhật (II).

Do đó diện tích hình chữ nhật MNPQ bằng tổng diện tích hai hình chữ nhật (I) và (II) là: ab + ac (đơn vị diện tích).

 Vậy a(b + c) = ab  +ac.

Giải Toán 7 trang 61 Tập 2

Hoạt động 3 trang 61 Toán 7 Tập 2:

Cho đơn thức P(x) = 2x và đa thức Q(x) = 3x² + 4x + 1.

a) Hãy nhân đơn thức P(x) với từng đơn thức của đa thức Q(x).

b) Hãy cộng các tích vừa tìm được:

Lời giải:

a) Đa thức Q(x) = 3x² + 4x + 1 nên các đơn thức của đa thức Q(x) là 3x²; 4x; 1.

Nhân đơn thức P(x) với từng đơn thức của đa thức Q(x) như sau:

2x . 3x² = 2 . 3 . x . x² = 6 . x¹⁺² = 6x³.

2x . 4x = 2 . 4 . x . x = 8 . x¹⁺¹ = 8x².

2x . 1 = 2x.

b) Cộng các tích vừa tìm được ta có:

2x . 3x² + 2x . 4x + 2x . 1

= 6x³ + 8x² + 2x.

Luyện tập 2 trang 61 Toán 7 Tập 2: Tính:

a) $\frac{1}{2}x(6x-4);$

b) $-x^2\left(\frac{1}{3}{x}^2-x-\frac{1}{4}\right).$

Lời giải:

a) $\frac{1}{2}x(6x-4)=\frac{1}{2}x.6x-\frac{1}{2}x.4$= $\frac{1}{2}$= = 3.x¹⁺¹  ‒ 2x = 3x² - 2x.

b) $-x^2\left(\frac{1}{3}{x}^2-x-\frac{1}{4}\right)=-x^2.\frac{1}{3}{x}^2-\left(-x^2\right).x-\left(-x^2\right).\frac{1}{4}$

$=-\frac{1}{3}{x}^{2+2}+x^{2+1}+\frac{1}{4}{x}^2=-\frac{1}{3}{x}^4+x^3+\frac{1}{4}{x}^2.$ 

Hoạt động 4 trang 61 Toán 7 Tập 2:

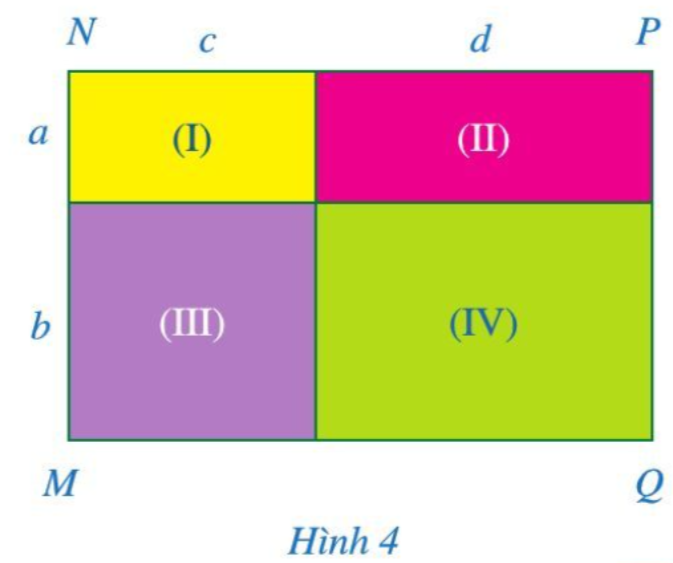
Quan sát hình chữ nhật MNPQ ở Hình 4.

a) Tính diện tích mỗi hình chữ nhật (I), (II), (III), (IV).

b) Tính diện tích của hình chữ nhật MNPQ.

c) So sánh: (a + b)(c + d) và ac + ad + bc + bd.

Lời giải:

a) Diện tích hình chữ nhật (I) là ac (đơn vị diện tích).

Diện tích hình chữ nhật (II) là ad (đơn vị diện tích).

Diện tích hình chữ nhật (III) là bc (đơn vị diện tích).

Diện tích hình chữ nhật (IV) là bd (đơn vị diện tích).

b) Quan sát Hình 4 ta có chiều rộng của hình chữ nhật MNPQ là a + b.

Chiều dài của hình chữ nhật MNPQ là c + d.

Diện tích hình chữ nhật MNPQ là (a + b)(c + d) (đơn vị diện tích).

c) Diện tích hình chữ nhật MNPQ bằng tổng diện của bốn hình chữ nhật (I), (II), (III), (IV) là: ac + ad + bc + bd (đơn vị diện tích).

Vậy (a + b)(c +  d) = ac + ad + bc + bd.

Giải Toán 7 trang 62 Tập 2

Hoạt động 5 trang 62 Toán 7 Tập 2:

Cho đa thức P(x) = 2x + 3 và đa thức Q(x) = x + 1.

a) Hãy nhân mỗi đơn thức của đa thức P(x) với từng đơn thức của đa thức Q(x).

b) Hãy cộng các tích vừa tìm được.

Lời giải:

a) Đa thức P(x) = 2x + 3 có các đơn thức là 2x; 3.

Đa thức Q(x) = x + 1 có các đơn thức là x; 1.

+ Nhân đơn thức 2x của đa thức P(x) với từng đơn thức của đa thức Q(x) như sau:

2x . x = 2x²;

2x . 1 = 2x;

+ Nhân đơn thức 3 của đa thức P(x) với từng đơn thức của đa thức Q(x) như sau:

3 . x = 3x;

3 . 1 = 3.

b) Cộng các tích vừa tìm được:

2x . x + 2x . 1 + 3 . x + 3 . 1

= 2x² + 2x + 3x + 3

= 2x² + (2x + 3x) + 3

= 2x² + 5x + 3.

Luyện tập 3 trang 62 Toán 7 Tập 2: Tính:

a) (x² - 6)(x² + 6);

b) (x - 1)(x² + x + 1).

Lời giải:

a) (x² - 6)(x² + 6)

= x² . x² + x² . 6 - 6 . x² - 6 . 6

= x⁴ + 6x² – 6x² – 36

= x⁴ + (6x² – 6x²) – 36

= x⁴ - 36.

Vậy (x² - 6)(x² + 6) = x⁴ - 36.

b) (x - 1)(x² + x + 1)

= x . x² + x . x + x . 1 - 1 . x² - 1 . x - 1 . 1

= x³ + x² + x - x² - x - 1

= x³ + (x² - x²) + (x - x) - 1

= x³ - 1

Vậy (x - 1)(x² + x + 1) = x³ - 1.

B. Bài tập

Giải Toán 7 trang 63 Tập 2

Bài 1 trang 63 Toán 7 Tập 2: Tính:

a) $\frac{1}{2}{x}^2.\frac{6}{5}{x}^3;$ 

b) $y^2\left(\frac{5}{7}{y}^3-2y^2+\mathrm{0,25}\right)$;

c) (2x² + x + 4)(x² - x - 1);

d) (3x - 4)(2x + 1) - (x - 2)(6x + 3).

Lời giải:

a) $\frac{1}{2}{x}^2.\frac{6}{5}{x}^3$

$=\frac{1}{2}.\frac{6}{5}.x^2.x^3$ 

$=\frac{\mathrm{1.2.3}}{2.5}.x^{2+3}$ 

$=\frac{3}{5}{x}^5.$

b) $y^2\left(\frac{5}{7}{y}^3-2y^2+\mathrm{0,25}\right)$

$=y^2.\frac{5}{7}{y}^3-y^2.2y^2+y^2\mathrm{.0,25}$ 

$=\frac{5}{7}.y^{2+3}-2y^{2+2}+\frac{25}{100}{y}^2$

$=\frac{5}{7}.y^5-2y^4+\frac{1}{4}{y}^2$ 

c) (2x² + x + 4)(x² - x - 1)

= 2x² . x² - 2x² . x - 2x² . 1 + x . x² - x . x - x . 1 + 4 . x² - 4 . x - 4 . 1

= 2x²⁺²  - 2x²⁺¹  - 2x² + x¹⁺² - x¹⁺¹ - x + 4x² - 4x - 4

= 2x⁴ - 2x³ - 2x² + x³ - x² - x + 4x² - 4x - 4

= 2x⁴ + (-2x³ + x³) + (-2x² - x²+ 4x²) + (-x - 4x) - 4

= 2x⁴ - x³ + x² - 5x - 4.

d) (3x - 4)(2x + 1) - (x - 2)(6x + 3)

= (3x . 2x + 3x . 1 - 4 . 2x - 4 . 1) - (x . 6x + x . 3 - 2 . 6x - 2 . 3)

= 6x² + 3x - 8x - 4 - (6x² + 3x - 12x - 6)

= 6x² + (3x - 8x) - 4 - [6x² + (3x −12x) - 6]

= 6x² - 5x - 4 - (6x² - 9x - 6)

= 6x² - 5x - 4 - 6x² + 9x + 6

= (6x² - 6x²) + (-5x + 9x) + (-4 + 6)

= 4x + 2.

Bài 2 trang 63 Toán 7 Tập 2:

Tìm bậc, hệ số cao nhất và hệ số tự do của mỗi đa thức sau:

a) P(x) = (-2x² - 3x + x - 1)(3x² - x - 2);

b) Q(x) = (x⁵ - 5)(-2x⁶ - x³ + 3).

Lời giải:

a) Ta thực hiện nhân và thu gọn rồi sắp xếp đa thức theo số mũ giảm dần của biến:

P(x) = (-2x² - 3x + x - 1)(3x² - x - 2)

= [-2x² + (-3x + x) - 1].(3x² - x - 2)

= (-2x² - 2x - 1)(3x² - x - 2)

= -2x².3x² - (-2x²).x - (-2x²).2 - 2x.3x² - 2x.(-x) - 2x.(-2) - 1.3x² - 1.(-x) - 1.(-2)

= -6x⁴ + 2x³ + 4x² - 6x³ + 2x² + 4x - 3x² + x + 2

= -6x⁴ + (2x³ - 6x³) + (4x² + 2x² - 3x²) + (4x + x) + 2

= -6x⁴ + (2 – 6)x³ + (4 + 2 – 3)x² + (4 + 1)x + 2

= -6x⁴ - 4x³ + 3x² + 5x + 2

Vậy đa thức P(x) có bậc bằng 4, hệ số cao nhất bằng -6 và hệ số tự do bằng 2.

b) Ta thực hiện nhân và thu gọn rồi sắp xếp đa thức theo số mũ giảm dần của biến:

Q(x) = (x⁵ - 5)(-2x⁶ - x³ + 3)

= x⁵ . (-2x⁶) - x⁵ . x³ + x⁵ . 3 - 5 . (-2x⁶) - 5 . (-x³) - 5 . 3

= -2x¹¹ - x⁸ + 3x⁵ + 10x⁶ + 5x³ - 15

= -2x¹¹ - x⁸ + 10x⁶ + 3x⁵ + 5x³ - 15

Khi đó đa thức Q(x) có bậc bằng 11, hệ số cao nhất bằng -2 và hệ số tự do bằng -15.

Bài 3 trang 63 Toán 7 Tập 2: Xét đa thức P(x) = x²(x² + x + 1) - 3x(x - a) + $\frac{1}{4}$ (với a là một số).

a) Thu gọn đa thức P(x) rồi sắp xếp đa thức đó theo số mũ giảm dần của biến.

b) Tìm a sao cho tổng các hệ số của đa thức P(x) bằng $\frac{5}{2}$.

Lời giải:

a) Ta có:

P(x) = x²(x² + x + 1) - 3x(x - a) + $\frac{1}{4}$

= x² . x² + x² . x + x² . 1 - (3x . x - 3x .a) + $\frac{1}{4}$

= x⁴ + x³ + x² - (3x² - 3ax) + $\frac{1}{4}$

= x⁴ + x³ + x² - 3x² + 3ax + $\frac{1}{4}$

= x⁴ + x³ + (x² - 3x²) + 3ax + $\frac{1}{4}$

= x⁴ + x³ - 2x² + 3ax + $\frac{1}{4}$

Vậy P(x) = x⁴ + x³ - 2x² + 3ax + $\frac{1}{4}$

b) Ta có đa thức P(x) = x⁴ + x³ - 2x² + 3ax + $\frac{1}{4}$ có các hệ số là: 1; 1; -2; 3a; $\frac{1}{4}$ 

Tổng các hệ số của đa thức P(x) là: $1+1+\left(-2\right)+3a+\frac{1}{4}=3a+\frac{1}{4}$ 

Do tổng các hệ số của đa thức P(x) bằng $\frac{5}{2}$ nên ta có 3a + $\frac{1}{4}$ = $\frac{5}{2}$.

Suy ra $3a=\frac{5}{2}-\frac{1}{4}=\frac{10}{4}-\frac{1}{4}=\frac{9}{4}$.

Do đó $a=\frac{9}{4}:3=\frac{9}{4}.\frac{1}{3}=\frac{3}{4}$.

Vậy $a=\frac{3}{4}.$ 

Bài 4 trang 63 Toán 7 Tập 2: Từ tấm bìa hình chữ nhật có kích thước 20 cm và 30 cm, bạn Quân cắt đi ở mỗi góc của tấm bìa một hình vuông sao cho bốn hình vuông bị cắt đi có cùng độ dài cạnh, sau đó gấp lại để tạo thành hình hộp chữ nhật không nắp (Hình 5).

Viết đa thức biểu diễn thể tích của hình hộp chữ nhật được tạo thành theo độ dài cạnh của hình vuông bị cắt đi.

Lời giải:

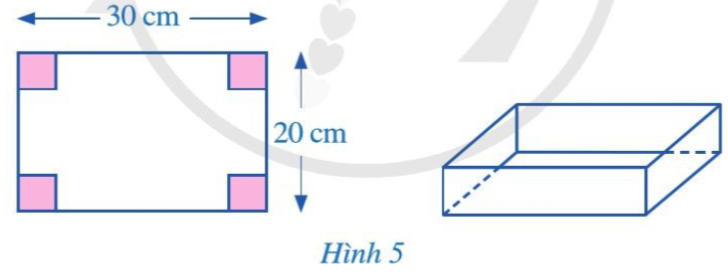
Gọi độ dài cạnh của hình vuông bị cắt đi là x (cm).

Ta thấy độ dài hai cạnh đáy của hình hộp chữ nhật là chiều dài và chiều rộng của hình chữ nhật sau khi cắt đi 2 hình vuông, chiều cao của hình hộp chữ nhật là độ dài cạnh của hình vuông.

Khi đó ta có:

- Chiều dài của hình chữ nhật sau khi cắt đi 2 hình vuông là 30 - 2a (cm).

- Chiều rộng của hình chữ nhật sau khi cắt đi 2 hình vuông là 20 - 2a (cm).

Do đó thể tích của hình hộp chữ nhật đó là: a(30 - 2a)(20 - 2a) (cm³).

Bài 5 trang 63 Toán 7 Tập 2:

Bạn Hạnh bảo với bạn Ngọc:

“- Nếu bạn lấy tuổi của một người bất kì cộng thêm 5;

- Được bao nhiêu đem nhân với 2;

- Lấy kết quả đó cộng với 10;

- Nhân kết quả vừa tìm được với 5;

- Đọc kết quả cuối cùng sau khi trừ đi 100. Mình sẽ đoán được tuổi của người đó.”

Em hãy sử dụng kiến thức nhân đa thức để giải thích vì sao bạn Hạnh lại đoán được tuổi người đó.

Lời giải:

Gọi tuổi của người đó là x (tuổi) (x > 0).

- Nếu lấy tuổi của người đó cộng thêm 5 ta được: x + 5.

- Nhân kết quả vừa tìm được với 2 ta có: (x + 5).2 = x.2 + 5.2 = 2x + 10.

- Lấy kết quả đó cộng với 10 ta được: 2x + 10 + 10 = 2x + 20.

- Nhân kết quả vừa tìm được với 5 ta có: (2x + 20).5 = 2x.5 + 20.5 = 10x + 100.

- Lấy kết quả trừ đi 100 ta được: 10x + 100 - 100 = 10x.

Do đó kết quả cuối cùng bằng 10 lần tuổi của người đó. Đó là lí do vì sao bạn Hạnh lại đoán được tuổi của người đó.

Xem thêm lời giải bài tập SGK Toán lớp 7 Cánh diều hay, chi tiết khác:

Bài 2: Đa thức một biến. Nghiệm của đa thức một biến

Bài 3: Phép cộng, phép trừ đa thức một biến

Bài 5: Phép chia đa thức một biến

Bài tập cuối chương 6

Bài 1: Tổng các góc của một tam giác