Giải SGK Toán 10 (Cánh Diều) Bài 5: Hai dạng phương trình quy về phương trình bậc hai

Giải Toán 10 Bài 5: Hai dạng phương trình quy về phương trình bậc hai

Câu hỏi khởi động

Câu hỏi khởi động trang 56 Toán lớp 10 Tập 1: Hai ô tô xuất phát tại cùng một điểm với vận tốc trung bình như nhau là 40 km/h từ hai vị trí A và B trên hai con đường vuông góc với nhau để đi về bến O là giao của hai con đường. Vị trí A cách bến 8 km, vị trí B cách bến 7 km. Gọi x là thời gian hai xe bắt đầu chạy cho tới khi cách nhau 5 km (Hình 31).

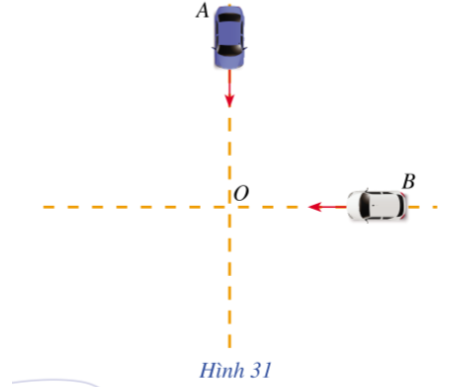
Bạn Dương xác định được x thỏa mãn phương trình $\sqrt{{\left(8-40x\right)}^2+{\left(7-40x\right)}^2}=5.$

Làm thế nào để tìm được giá trị của x?

Lời giải:

Sau bài học này ta sẽ giải quyết bài toán này như sau:

Để tìm được giá trị của x, ta cần giải phương trình $\sqrt{{\left(8-40x\right)}^2+{\left(7-40x\right)}^2}=5$ (1).

Điều kiện xác định: (8 – 40x)² + (7 – 40x)² ≥ 0.

Vì (8 – 40x)² ≥ 0 và (7 – 40x)² ≥ 0 với mọi x nên (8 – 40x)² + (7 – 40x)² ≥ 0 với mọi x.

Bình phương hai vế ta được: (8 – 40x)² + (7 – 40x)² = 25

⇔ 1 600x² – 640x + 64 + 1 600x² – 560x + 49 = 25

⇔ 3 200x² – 1 200x + 88 = 0

⇔ 400x² – 150x + 11 = 0

$\iff \left[\begin{array}{l}x=0,1\\ x=0,275\end{array}\right.$(thỏa mãn điều kiện)

Vậy có hai giá trị của x: x = 0,1 hoặc x = 0,275 nghĩa là có hai thời điểm để hai xe cách nhau 5km.

1. Giải phương trình có dạng $\sqrt{f\left(x\right)}$=$\sqrt{g\left(x\right)}$ (I)

Luyện tập 1 trang 57 Toán lớp 10 Tập 1: Giải phương trình:

$\sqrt{3x^2-4x+1}=\sqrt{x^2+x-1} \left(1\right).$

Lời giải:

Bình phương hai vế của phương trình (1) ta được:

3x² – 4x + 1 = x² + x – 1

⇔ 2x² – 5x + 2 = 0

$\iff \left[\begin{array}{l}x=2\\ x=\frac{1}{2}\end{array}\right.$.

Thay x = 2 vào bất phương trình 3x² – 4x + 1 ≥ 0 ta được: 3.2² – 4.2 + 1 ≥ 0 ⇔ 5 ≥ 0 (luôn đúng). Do đó x = 2 là nghiệm của phương trình (1).

Thay $x=\frac{1}{2}$ vào bất phương trình 3x² – 4x + 1 ≥ 0 ta được: $3.{\left(\frac{1}{2}\right)}^2-4.\frac{1}{2}+1\ge 0\iff \frac{3}{4}-2+1\ge 0\iff -\frac{1}{4}\ge 0$ (vô lý). Do đó $x=\frac{1}{2}$ không là nghiệm của phương trình (1).

Vậy phương trình (1) có nghiệm là x = 2.

2. Giải phương trình có dạng $\sqrt{f\left(x\right)}$=g(x) (II)

Luyện tập 2 trang 58 Toán lớp 10 Tập 1: Giải phương trình:

$\sqrt{3x-5}=x-1$ (1)

Lời giải:

Ta có:  x – 1 ≥ 0 ⇔ x ≥ 1.

Bình phương hai vế của (1) ta được:

 3x – 5 = (x – 1)²

⇔ 3x – 5 = x² – 2x + 1

⇔ x² – 5x + 6 = 0

$\iff \left[\begin{array}{l}x=2\\ x=3\end{array}\right.$ (thỏa mãn x ≥ 1)

Vậy phương trình đã cho có hai nghiệm là x = 2 và x = 3.

Bài tập

Bài 1 trang 58 Toán lớp 10 Tập 1: Giải các phương trình sau:

a) $\sqrt{2x-3} = \sqrt{2x^2-3x-1}$;

b) $\sqrt{4x^2-6x-6}=\sqrt{x^2-6}$;

c) $\sqrt{x+9}=2x-3$;

d) $\sqrt{-x^2+4x-2}=2-x$.

Lời giải:

a) $\sqrt{2x-3} = \sqrt{2x^2-3x-1}$

Bình phương hai vế của phương trình đã cho ta được:

2x –  3 = 2x2 – 3x – 1

⇔ 2x² – 3x – 1 – 2x + 3 = 0

⇔ 2x² – 5x +2 = 0

$\iff \left[\begin{array}{l}x=\frac{1}{2}\\ x=2\end{array}\right.$

Lần lượt thay hai giá trị trên vào bất phương trình 2x² – 3x – 1 ≥ 0 ta thấy chỉ có giá trị x = 2 thỏa mãn bất phương trình.

Vậy phương trình đã cho có nghiệm là x = 2.

b) $\sqrt{4x^2-6x-6}=\sqrt{x^2-6}$ 

Bình phương hai vế của phương trình đã cho ta được:

4x² – 6x – 6 = x² – 6

⇔ 4x² – x² – 6x – 6 + 6 = 0

⇔ 3x² – 6x = 0

⇔ 3x(x – 2) = 0

$\iff \left[\begin{array}{l}x=0\\ x-2=0\end{array}\right.\iff \left[\begin{array}{l}x=0\\ x=2\end{array}\right.$

Lần lượt thay hai giá trị trên vào bất phương trình 4x² – 6x – 6 ≥ 0 ta thấy cả hai giá trị đều không thỏa mãn bất phương trình.

Vậy phương trình đã cho vô nghiệm.

c) $\sqrt{x+9}=2x-3$  

Điều kiện: 2x – 3 ≥ 0 ⇔ x ≥ $\frac{3}{2}$ (1)

Bình phương cả hai vế của phương trình đã cho ta được:

x + 9 = (2x – 3)²

⇔ x + 9 = 4x² – 12x + 9

⇔ 4x² – 12x + 9 – x – 9 = 0

⇔ 4x² – 13x = 0

⇔ x(4x – 13) = 0

$\iff \left[\begin{array}{l}x=0\\ 4x-13=0\end{array}\right.\iff \left[\begin{array}{l}x=0\\ x=\frac{13}{4}\end{array}\right.$

Ta thấy chỉ có giá trị x = $\frac{13}{4}$ thỏa mãn điểu kiện (1).

Vậy nghiệm của phương trình đã cho là x = $\frac{13}{4}$.

d) $\sqrt{-x^2+4x-2}=2-x$ 

Điều kiện: 2 – x ≥ 0 ⇔ x ≤ 2 (2).

Bình phương hai vế của phương trình đã cho ta được:

– x² + 4x – 2 = (2 – x)²

⇔ – x² + 4x – 2 = 4 – 4x + x²

⇔ 2x² – 8x + 6 = 0

⇔ x² – 4x + 3 = 0

$\iff \left[\begin{array}{l}x=3\\ x=1\end{array}\right.$

Ta thấy trong hai giá trị trên chỉ có giá trị x = 1 thỏa mãn điều kiện (2).

Vậy nghiệm của phương trình đã cho là x = 1.

Bài 2 trang 59 Toán lớp 10 Tập 1: Giải các phương trình sau:

a) $\sqrt{2-x}+2x=3$;

b) $\sqrt{-x^2+7x-6}+x=4$.

Lời giải:

a) $\sqrt{2-x}+2x=3$

 $\iff \sqrt{2-x}=3-2x$(1)

Điều kiện: 3 – 2x ≥ 0 ⇔ x ≤ $\frac{3}{2}$ (2).

Bình phương hai vế của phương trình (1) ta được: 2 – x = (3 – 2x)²

⇔ 2 – x = 9 – 12x + 4x²

⇔ 4x² – 11x + 7 = 0

$\iff \left[\begin{array}{l}x=1\\ x=\frac{7}{4}\end{array}\right.$

Ta thấy x = 1 thỏa mãn (2) và $x=\frac{7}{4}$ không thỏa mãn (2).

Vậy nghiệm của phương trình đã cho là x = 1.

b) $\sqrt{-x^2+7x-6}+x=4$    

$\iff \sqrt{-x^2+7x-6}=4-x$ (3)

Điều kiện: 4 – x ≥ 0 ⇔ x ≤ 4 (4)

 Bình phương hai vế của phương trình (3) ta được: – x² + 7x – 6 = (4 – x)²

⇔ – x² + 7x – 6 = 16 – 8x + x²

⇔ 2x² – 15x + 22 = 0

$\iff \left[\begin{array}{l}x=2\\ x=\frac{11}{2}\end{array}\right.$

Ta thấy x = 2 thỏa mãn (4) và $x=\frac{11}{2}$ không thỏa mãn (4).

Vậy nghiệm của phương trình đã cho là x = 2.

Bài 3 trang 59 Toán lớp 10 Tập 1: Để leo lên một bức tường, bác Nam dùng một chiếc thang có chiều dài cao hơn bức tường đó 1 m. Ban đầu, bác Nam đặt chiếc thang mà đầu trên của chiếc thang đó vừa chạm đúng và mép trên bức tường (Hình 33a). Sau đó, bác Nam dịch chuyển chân thang vào gần chân tường thêm 0,5 m thì bác Nam nhận thấy thang tạo với mặt đất một góc 60° (Hình 33b). Bức tường cao bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?

Lời giải:

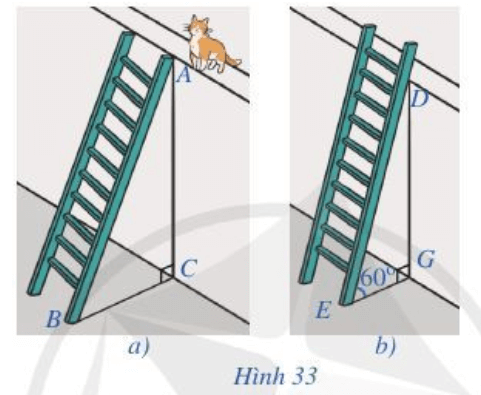
Gọi chiều cao của bức tường là x (mét) (x > 0).

Vì chiếc thang cao hơn tường 1 m nên chiều cao của chiếc thang là x + 1 (m).

Hình 33a) tương ứng ta có: AC = x, AB = x + 1

Xét tam giác ABC vuông tại C:

AB² = AC² + BC² (định lý Pythagore)

⇒ BC² = AB² – AC² = (x + 1)² – x² = (x + 1 – x)(x + 1 + x) = 2x + 1

$\Rightarrow BC=\sqrt{2x+1}$ (m).

Hình 33b) ta thấy chiều cao bức tường không thay đổi nên DG = x (m).

Khi bác Nam dịch chuyển chân thang vào gần tường thêm 0,5 m thì GE = BC – 0,5.

Suy ra $GE=\sqrt{2x+1}-0,5$  (m)

Xét tam giác DGE vuông tại G, ta có:

$\tan \widehat{DEG}=\frac{DG}{GE}$

⇔ $\tan 60°=\frac{x}{\sqrt{2x+1}-0,5}$

⇔$\sqrt{3}=\frac{x}{\sqrt{2x+1}-0,5}$

⇔$x=\sqrt{3}\left(\sqrt{2x+1}-0,5\right)$

$\iff x=\sqrt{3\left(2x+1\right)}-\frac{\sqrt{3}}{2}$

$\iff \sqrt{3\left(2x+1\right)}=x+\frac{\sqrt{3}}{2}$   (1)

Điều kiện $x+\frac{\sqrt{3}}{2}\ge 0\iff x\ge -\frac{\sqrt{3}}{2}$ (2)

Bình phương hai vế của (1) ta được: $3\left(2x+1\right)={\left(x+\frac{\sqrt{3}}{2}\right)}^2$

$\iff 6x+3=x^2+\sqrt{3}x+\frac{3}{4}$

$\iff x^2+\left(\sqrt{3}-6\right)x-\frac{9}{4}=0$ 

$\iff \left[\begin{array}{l}x=\frac{6-\sqrt{3}+\sqrt{48-12\sqrt{3}}}{2}\approx 4,7\\ x=\frac{6-\sqrt{3}-\sqrt{48-12\sqrt{3}}}{2}\approx -0,5\end{array}\right.$ 

Ta thấy chỉ có x ≈ 4,7 thỏa mãn x > 0 và điều kiện (2).

Vậy bức tường cao khoảng 4,7 m.

Bài 4 trang 59 Toán lớp 10 Tập 1: Một người đứng ở điểm A trên bờ sông rộng 300 m, chèo thuyền đến vị trí D, sau đó chạy bộ đến vị trí B cách C một khoảng 800 m như Hình 34. Vận tốc chèo thuyền là 6 km/h, vận tốc chạy bộ là 10 km/h và giả sử vận tốc dòng nước không đáng kể. Tính khoảng cách từ vị trí C đến D, biết tổng thời gian người đó chèo thuyền và chạy bộ từ A đến B là 7,2 phút.

Lời giải:

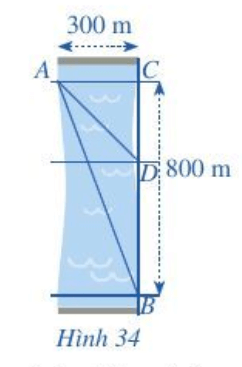
Gọi độ dài khoảng cách từ vị trí C đến D là x (km, x > 0).

Đổi: 300 m = 0,3 km; 800 m = 0,8 km; 7,2 phút = 0,12 giờ.

Tương ứng ta có: AC = 0,3 km; CD = x km; BC = 0,8 km; DB = BC – CD = 0,8 – x (km).

Xét tam giác ACD vuông tại C, ta có:

AD² = AC² + CD² (định lý Pythagore)

AD² = (0,3)² + x² = 0,09 + x²

$\Rightarrow AD=\sqrt{0,09+x^2}$ (km)

Thời gian người đó chèo thuyền từ vị trí A đến vị trí D là $\frac{\sqrt{0,09+x^2}}{6}$ (giờ).

Thời gian người đó chạy bộ từ vị trí D đến vị trí B là $\frac{0,8-x}{10}$ (giờ).

Tổng thời gian người đó chèo thuyền và đi bộ là $\frac{\sqrt{0,09+x^2}}{6}+\frac{0,8-x}{10}$ (giờ).

Vì người đó mất 0,12 giờ chèo thuyền và chạy bộ từ A đến B nên ta có phương trình:

$\frac{\sqrt{0,09+x^2}}{6}+\frac{0,8-x}{10}=0,12$

$\iff \frac{5\sqrt{0,09+x^2}}{30}+\frac{3\left(0,8-x\right)}{30}=0,12$

$\iff 5\sqrt{0,09+x^2}+2,4-3x=3,6$

$\iff 5\sqrt{0,09+x^2}=1,2+3x$   (1)

Điều kiện 1,2 + 3x ≥ 0 ⇔ $x\ge -\frac{2}{5}$ (2)

Bình phương cả hai vế của (1) ta được: 25.(0,09 + x²) = (1,2 + 3x)²

⇔ 2,25 + 25x² = 1,44 + 7,2x + 9x²

⇔ 16x² – 7,2x + 0,81 = 0

⇔ x = 0,225 (thỏa mãn điều kiện x > 0 và điều kiện (2))

Ta có: x = 0,225 km = 225 m.

Vậy khoảng cách từ vị trí C đến D là 225 m. 

Bài 5 trang 59 Toán lớp 10 Tập 1: Một ngọn hải đăng đặt tại vị trí A cách bờ biển một khoảng cách AB = 4 km. Trên bờ biển có một cái kho ở vị trí C cách B một khoảng là 7 km. Người canh hải đăng có thể chèo thuyền từ A đến vị trí M trên bờ biển với vận tốc 3 km/h rồi đi bộ đến C với vận tốc 5 km/h như Hình 35. Tính khoảng cách từ vị trí B đến M, biết thời gian người đó đi từ A đến C là 148 phút.

Lời giải:

Gọi khoảng cách từ vị trí B đến M là x (km, x > 0).

Tương ứng trên hình vẽ ta có: AB = 4 km, BM = x km, BC = 7 km.

Xét tam giác ABM vuông tại B, ta có:

AM² = AB² + BM² (định lý Pythagore)

⇔ AM² = 42 + x² = 16 + x²

$\Rightarrow AM=\sqrt{16+x^2}$(km)

Thời gian chèo thuyền từ A đến M là $\frac{\sqrt{16+x^2}}{3}$ (giờ).

Ta có: MC = BC – BM = 7 – x (km).

Thời gian đi bộ từ M đến C là $\frac{7-x}{5}$ (giờ).

Tổng thời gian người đó đi từ A đến C là: $\frac{\sqrt{16+x^2}}{3}+\frac{7-x}{5}$ (giờ)

Biết thời gian đi từ A đến C là 148 phút = $\frac{37}{15}$ giờ nên ta có phương trình: $\frac{\sqrt{16+x^2}}{3}+\frac{7-x}{5}=\frac{37}{15}$

$\iff \frac{5\sqrt{16+x^2}}{15}+\frac{3.\left(7-x\right)}{15}=\frac{37}{15}$

$\iff 5\sqrt{16+x^2}+3.\left(7-x\right)=37$

$\iff 5\sqrt{16+x^2}+21-3x=37$

$\iff 5\sqrt{16+x^2}=16+3x$  (1)

Điều kiện 16 + 3x ≥ 0 ⇔ x ≥ $-\frac{16}{3}$ (2)

Bình phương cả hai vế của (1) ta được: 25.(16 + x²) = (16 + 3x)²

⇔ 400 + 25x² = 256 + 96x + 9x²

⇔ 16x² – 96x + 144 = 0

 ⇔ x = 3 (thỏa mãn điều kiện x > 0 và (2))

Vậy khoảng cách từ vị trí B đến vị trí M là 3 km.

Xem thêm lời giải bài tập SGK Toán lớp 10 Cánh Diều hay, chi tiết khác:

Bài 3: Dấu của tam thức bậc hai

Bài 4: Bất phương trình bậc hai một ẩn

Bài tập cuối chương 3

Bài 1: Giá trị lượng giác của một góc từ 0 độ đến 180 độ. Định lý côsin và định lý sin trong tam giác

Bài 2: Giải tam giác. Tính diện tích tam giác