Một người đứng ở điểm A trên bờ sông rộng 300 m, chèo thuyền đến vị trí D, sau đó chạy bộ đến vị trí B cách C một khoảng 800 m như Hình 34

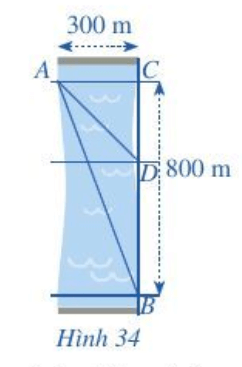
Bài 4 trang 59 Toán lớp 10 Tập 1: Một người đứng ở điểm A trên bờ sông rộng 300 m, chèo thuyền đến vị trí D, sau đó chạy bộ đến vị trí B cách C một khoảng 800 m như Hình 34. Vận tốc chèo thuyền là 6 km/h, vận tốc chạy bộ là 10 km/h và giả sử vận tốc dòng nước không đáng kể. Tính khoảng cách từ vị trí C đến D, biết tổng thời gian người đó chèo thuyền và chạy bộ từ A đến B là 7,2 phút.

Trả lời

Gọi độ dài khoảng cách từ vị trí C đến D là x (km, x > 0).

Đổi: 300 m = 0,3 km; 800 m = 0,8 km; 7,2 phút = 0,12 giờ.

Tương ứng ta có: AC = 0,3 km; CD = x km; BC = 0,8 km; DB = BC – CD = 0,8 – x (km).

Xét tam giác ACD vuông tại C, ta có:

AD² = AC² + CD² (định lý Pythagore)

AD² = (0,3)² + x² = 0,09 + x²

$\Rightarrow AD=\sqrt{0,09+x^2}$ (km)

Thời gian người đó chèo thuyền từ vị trí A đến vị trí D là $\frac{\sqrt{0,09+x^2}}{6}$ (giờ).

Thời gian người đó chạy bộ từ vị trí D đến vị trí B là $\frac{0,8-x}{10}$ (giờ).

Tổng thời gian người đó chèo thuyền và đi bộ là $\frac{\sqrt{0,09+x^2}}{6}+\frac{0,8-x}{10}$ (giờ).

Vì người đó mất 0,12 giờ chèo thuyền và chạy bộ từ A đến B nên ta có phương trình:

$\frac{\sqrt{0,09+x^2}}{6}+\frac{0,8-x}{10}=0,12$

$\iff \frac{5\sqrt{0,09+x^2}}{30}+\frac{3\left(0,8-x\right)}{30}=0,12$

$\iff 5\sqrt{0,09+x^2}+2,4-3x=3,6$

$\iff 5\sqrt{0,09+x^2}=1,2+3x$   (1)

Điều kiện 1,2 + 3x ≥ 0 ⇔ $x\ge -\frac{2}{5}$ (2)

Bình phương cả hai vế của (1) ta được: 25.(0,09 + x²) = (1,2 + 3x)²

⇔ 2,25 + 25x² = 1,44 + 7,2x + 9x²

⇔ 16x² – 7,2x + 0,81 = 0

⇔ x = 0,225 (thỏa mãn điều kiện x > 0 và điều kiện (2))

Ta có: x = 0,225 km = 225 m.

Vậy khoảng cách từ vị trí C đến D là 225 m. 

Xem thêm lời giải bài tập SGK Toán lớp 10 Cánh Diều hay, chi tiết khác:

Bài 3: Dấu của tam thức bậc hai

Bài 4: Bất phương trình bậc hai một ẩn

Bài 5: Hai dạng phương trình quy về phương trình bậc hai

Bài tập cuối chương 3

Bài 1: Giá trị lượng giác của một góc từ 0 độ đến 180 độ. Định lý côsin và định lý sin trong tam giác

Bài 2: Giải tam giác. Tính diện tích tam giác