Giải SGK Toán 10 (Cánh Diều): Bài tập cuối chương 3 trang 60, 61

Giải Toán 10: Bài tập cuối chương 3 trang 60, 61

Bài 1 trang 60 Toán lớp 10 Tập 1: Tìm tập xác định của mỗi hàm số sau:

a) $y=\frac{1}{x^2-x}$

b) $y=\sqrt{x^2-4x+3}$

c) $y=\frac{1}{\sqrt{x-1}}$

Lời giải:

a) Biểu thức $\frac{1}{x^2-x}$ xác định khi x² – x ≠ 0 ⇔ x(x – 1) ≠ 0 $\iff \left\{\begin{array}{l}x\ne 0\\ x\ne 1\end{array}\right.$.

Vậy tập xác định của hàm số là D = {x $\in ℝ$| x ≠ 0, x ≠ 1} = $ℝ\backslash \left\{0;1\right\}$.

b) Biểu thức $\sqrt{x^2-4x+3}$ xác định khi x² – 4x + 3 ≥ 0 (1).

Xét tam thức bậc hai x² – 4x + 3 có hệ số a = 1 > 0, b = – 4, c = 3 và ∆ = (– 4)² – 4 . 1 . 3 = 4 > 0.

Suy ra tam thức có hai nghiệm phân biệt x₁ = 1, x₂ = 3

Khi đó ta có bảng xét dấu:

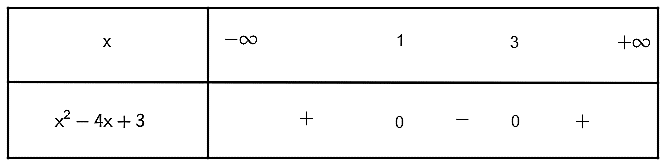
Suy ra x² – 4x + 3 ≥ 0 khi và khi chỉ khi x ≤ 1 và x ≥ 3.

Vậy tập xác định của hàm số đã cho là D = (– ∞; 1] ∪ [3; + ∞).

c) Biểu thức $\frac{1}{\sqrt{x-1}}$ xác định khi $\left\{\begin{array}{l}x-1\ge 0\\ \sqrt{x-1}\ne 0\end{array}\right.$⇔ x – 1 > 0 ⇔ x > 1.

Vậy tập xác định của hàm số đã cho là D = (1; + ∞).

Bài 2 trang 60 Toán lớp 10 Tập 1: Đồ thị ở Hình 36 cho thấy sự phụ thuộc của lượng hàng hóa được sản xuất (cung) (đơn vị: sản phẩm) bởi giá bán (đơn vị: triệu đồng/sản phẩm) đối với một loại hàng hóa.

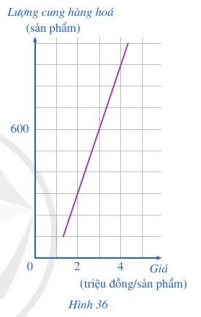
a) Xác định lượng hàng hóa được sản xuất khi mức giá bán 1 sản phẩm là 2 triệu đồng; 4 triệu đồng.

b) Biết nhu cầu thị trường đang cần 600 sản phẩm. Hỏi với mức giá bán là bao nhiêu thì thị trường cân bằng (thị trường cân bằng khi sản lượng cung bằng sản lượng cầu)? 

Lời giải:

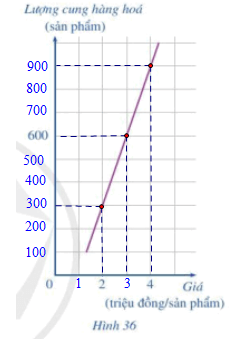
Hoàn thiện các giá trị trên hai trục ta được đồ thị sau:

a) Dựa vào đồ thị trên, ta có:

Khi mức giá bán 1 sản phẩm là 2 triệu đồng thì lượng hàng hóa được sản xuất tương ứng là 300 sản phẩm.

Khi mức giá bán 1 sản phẩm là 4 triệu đồng thì lượng hàng hóa được sản xuất tương ứng là 900 sản phẩm.

b) Để thị trường cân bằng thì sản lượng cung bằng sản lượng cầu mà nhu cầu thị trường đang cần 600 sản phẩm nên mức giá bán là 3 triệu đồng.

Bài 3 trang 60 Toán lớp 10 Tập 1: Một nhà cung cấp dịch vụ Internet đưa ra hai gói khuyến mại cho người dùng như sau:

Gói A: Giá cước 190 000 đồng/tháng.

Nếu trả tiền cước ngay 6 tháng thì sẽ được tặng thêm 1 tháng. 

Nếu trả tiền cước ngay 12 tháng thì sẽ được tặng thêm 2 tháng. 

Gói B: Giá cước 189 000 đồng/tháng.

Nếu trả tiền cước ngay 7 tháng thì số tiền phải trả cho 7 tháng đó là 1 134 000 đồng. 

Nếu trả tiền cước ngay 15 tháng thì số tiền phải trả cho 15 tháng đó là 2 268 000 đồng. 

Giả sử số tháng sử dụng Internet là x (x nguyên dương). 

a) Hãy lập các hàm số thể hiện số tiền phải trả ít nhất theo mỗi gói A, B nếu thời gian dùng không quá 15 tháng. 

b) Nếu gia đình bạn Minh dùng 15 tháng thì nên chọn gói nào? 

Lời giải:

a) Giả sử số tháng sử dụng Internet là x (x nguyên dương, x ≤ 15).

Gọi y (đồng, y > 0) là số tiền phải trả khi dùng Internet.

Theo gói A, ta có:

+ Nếu x ≤ 6: y = 190 000.x

+ Nếu 6 < x ≤ 13: y = 190 000 . (x – 1)

+ Nếu 13 < x ≤ 15: y = 190 000 . (x – 2)

Vậy ta có hàm số thể hiện số tiền ít nhất phải trả theo gói A là:

$y=\left\{\begin{array}{l}190000.xkhix\le 6\\ 190000.\left(x-1\right)khi6<x\le 13\\ 190000.\left(x-2\right)khi13<x\le 15\end{array}\right.$.

Theo gói B, ta có:

+ Nếu x < 7: y = 189 000 . x

 + Nếu x = 7: y = 1 134 000

+ Nếu 7 < x < 13: y = 1 134 000 + (x – 7) . 189 000

+ Nếu 13 ≤ x ≤ 15: y = 2 268 000

Vậy ta có hàm số thể hiện số tiền ít nhất phải trả theo gói B là:

$y=\left\{\begin{array}{l}189000.xkhix<7\\ 1134000khix=7\\ 1134000+\left(x-7\right).189000khi7<x<13\\ 2268000khi13\le x\le 15\end{array}\right.$.

b) Gia đình Minh dùng 15 tháng nên x = 15

Theo gói A:

 Với x = 15 tháng thì số tiền cước trả ít nhất là:

190 000.(15 – 2) = 2 470 000 (đồng)

Do đó với 15 tháng sử dụng Internet theo gói cước A thì gia đình bạn Minh phải trả 2 470 000 đồng.

Theo gói B:

Với x = 15 tháng thì số tiền cước phải trả ít nhất là: 2 268 000 (đồng)

Do đó nếu sử dụng gói cước B thì gia đình bạn Minh phải trả số tiền ít nhất là 2 268 000 đồng.

Vì 2 268 000 < 2 470 000 nên dùng gói cước B giá thấp hơn.

Vậy gia đình bạn Minh nếu dùng 15 tháng thì nên chọn gói B để số tiết kiệm chi phí nhất.

Bài 4 trang 60, 61 Toán lớp 10 Tập 1: Quan sát đồ thị hàm số bậc hai y = ax² + bx + c ở Hình 37a và Hình 37b rồi nêu:

a) Dấu của hệ số a;

b) Tọa độ đỉnh và trục đối xứng;

c) Khoảng đồng biến;

d) Khoảng nghịch biến;

e) Khoảng giá trị x mà y > 0;

g) Khoảng giá trị x mà y ≤ 0. 

Lời giải:

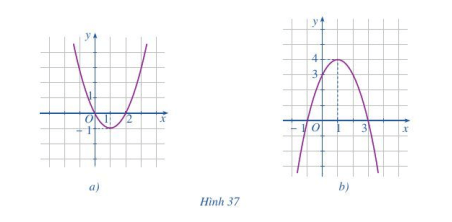
* Hình 37a: Quan sát đồ thị ta thấy:

a) Bề lõm của đồ thị hướng lên trên nên hệ số a > 0 hay hệ số a mang dấu “+”.

b) Tọa độ đỉnh I(1; – 1), trục đối xứng x = 1.

c) Trên khoảng (1; + ∞) đồ thị hàm số đi lên nên hàm số đồng biến trên khoảng (1; + ∞).

d) Trên khoảng (– ∞; 1) đồ thị hàm số đi xuống nên hàm số nghịch biến trên khoảng (– ∞; 1).

e) Trên các khoảng (– ∞; 0) và (2; + ∞) phần Parabol nằm phía trên trục hoành nên hàm số y > 0 với x ∈ (– ∞; 0) ∪ (2; + ∞).

g) Trên khoảng (0; 2) phần parabol  nằm phía dưới trục hoành nên hàm số y < 0 với x ∈ (0; 2) và f(x) = 0 tại x = 0 hoặc x = 2. Do đó khoảng giá trị của x mà y ≤ 0 là đoạn [0; 2].

* Hình 37b: Quan sát đồ thị ta thấy,

a) Bề lõm của đồ thị hướng xuống dưới nên a < 0 hay hệ số a mang dấu “–”.

b) Tọa độ đỉnh I(1; 4), trục đối xứng x = 1.

c) Trong khoảng (– ∞; 1) phần parabol đi lên nên hàm số đồng biến trên khoảng (– ∞; 1).

d) Trong khoảng (1; +∞) phần parabol đi xuống nên hàm số nghịch biến trên khoảng (1; +∞).

e) Trong khoảng (– 1; 3) phần parabol nằm phía trên trục hoành nên y > 0 khi  x ∈ (– 1; 3).

g) Trong khoảng (– ∞; – 1) và (3; + ∞) phần parabol nằm phía dưới trục hoành nên để y ≤ 0 khi x ∈ (– ∞; – 1] ∪ [3; + ∞).

Bài 5 trang 61 Toán lớp 10 Tập 1: Vẽ đồ thị của mỗi hàm số sau:

a) y = x² – 3x – 4; 

b) y = x² + 2x + 1; 

c) y = – x² + 2x – 2. 

Lời giải:

a) y = x² – 3x – 4

Ta có: hệ số a = 1 > 0, b = – 3, c = – 4, ∆ = (– 3)² – 4 . 1 . (– 4) = 25 > 0.

- Parabol có bề lõm hướng lên trên.

- Tọa độ đỉnh I$\left(\frac{3}{2};\frac{-25}{4}\right)$.

- Trục đối xứng $x=\frac{3}{2}$.

- Ta có bảng giá trị sau:

Đồ thị hàm số y = x² – 3x – 4 là đường cong đi qua các điểm B(-1; 0), A(0; -4); $I\left(\frac{3}{2};\frac{-25}{4}\right)$; D(3; -4) và C(4; 0).

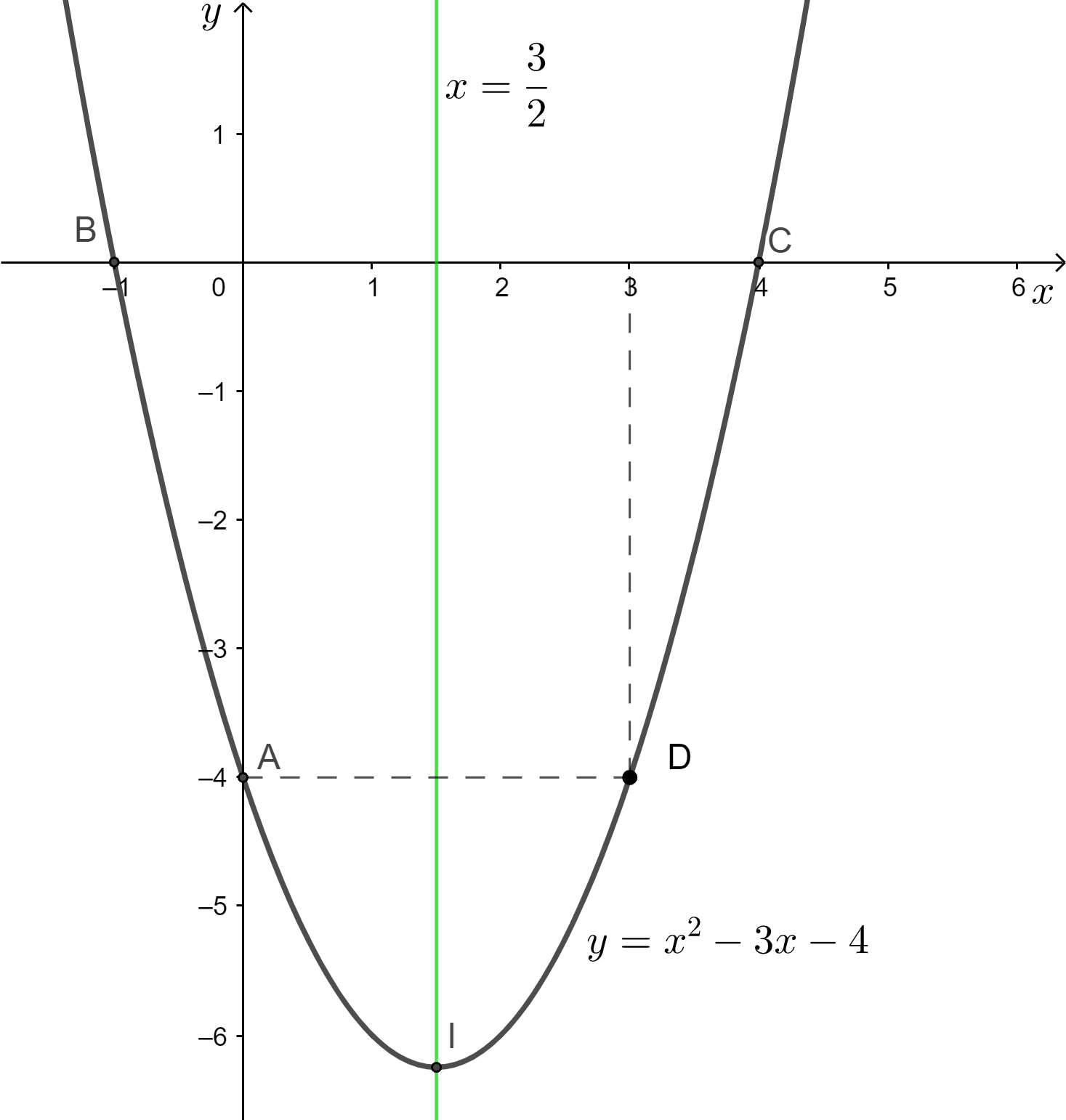
b) y = x² + 2x + 1

Ta có hệ số a = 1 > 0, b = 2, c = 1, ∆ = 2² – 4 . 1 . 1 = 0.

- Parabol có bề lõm hướng lên trên.

- Tọa độ đỉnh I(– 1; 0).

- Trục đối xứng x = – 1.

- Ta có bảng giá trị sau:

Đồ thị hàm số y = x² + 2x + 1 là đường cong đi qua các điểm A(-3; 4), B(-2; 1); I(-1; 0); C(0; 1) và D(1; 4).

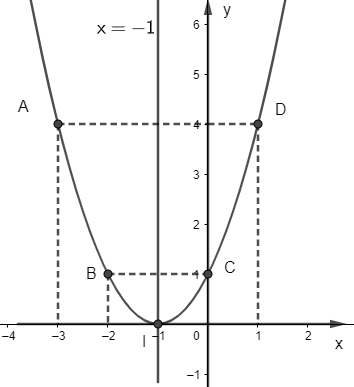
c) y = – x² + 2x – 2

Ta có hệ số a = – 1 < 0, b = 2, c = – 2 và ∆ = 2² – 4 . (– 1) . (– 2) = – 4.

- Đồ thị hàm số có bề lõm hướng xuống dưới.

- Tọa độ đỉnh I(1; – 1).

- Trục đối xứng x = 1.

- Ta có bảng sau:

Đồ thị hàm số y = - x² + 2x - 2 là đường cong đi qua các điểm A(-1; -5), B(0; -2); I(1; -1); C(2; -2) và C(3; -5).

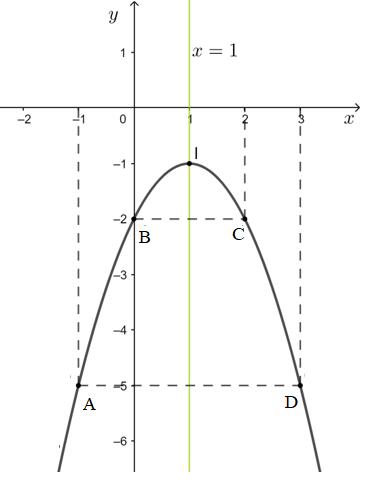
Bài 6 trang 61 Toán lớp 10 Tập 1: Lập bảng xét dấu của mỗi tam thức bậc hai sau:

a) f(x) = – 3x² + 4x – 1; 

b) f(x) = x² – x – 12; 

c) f(x) = 16x² + 24x + 9. 

Lời giải:

a) Xét tam thức bậc hai f(x) = – 3x² + 4x – 1 có:

∆ = 4² – 4 . (– 3) . (– 1) = 4 > 0.

Do đó tam thức f(x) có hai nghiệm phân biệt x₁ = $\frac{1}{3}$ và x₂ = 1

Ta lại có a = - 3 < 0

Ta lập được bảng xét dấu như sau:

b) Xét tam thức bậc hai f(x) = x² – x – 12 có:

 ∆ = (– 1)² – 4 . 1 . (– 12) = 49 > 0.

Do đó tam thức f(x) có hai nghiệm phân biệt x₁ = – 3 và x₂ = 4.

Ta có hệ số a = 1 > 0

Ta lập được bảng xét dấu sau:

c) Xét tam thức bậc hai f(x) = 16x² + 24x + 9 có:

∆ = 24² – 4 . 16 . 9 = 0.

Do đó tam thức bậc hai có nghiệm kép x = $-\frac{3}{4}$.

Ta có hệ số a = 16 > 0

Sử dụng định lý về dấu của tam thức bậc hai, ta có bảng xét dấu sau:

Bài 7 trang 61 Toán lớp 10 Tập 1: Giải các bất phương trình sau:

a) 2x² + 3x + 1 ≥ 0; 

b) – 3x² + x + 1 > 0; 

c) 4x² + 4x + 1 ≥ 0; 

d) – 16x² + 8x – 1 < 0; 

e) 2x² + x + 3 < 0; 

g) – 3x² + 4x – 5 < 0. 

Lời giải:

a) Xét tam thức bậc hai 2x² + 3x + 1 có ∆ = 3² – 4 . 2 . 1 = 1 > 0

Suy ra tam thức này có hai nghiệm x₁ = – 1, x₂ = $-\frac{1}{2}$ 

Ta có hệ số a = 2 > 0.

Khi đó ta có bảng xét dấu sau:

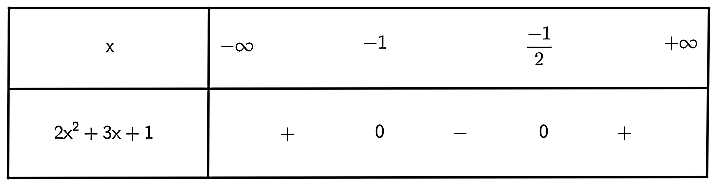
Ta thấy tam thức 2x² + 3x + 1 không âm khi x ≤ -1 hoặc $x\ge -\frac{1}{2}$.

Vậy tập nghiệm của bất phương trình đã cho là $\left(-\infty ;-1\right]\cup \left[-\frac{1}{2};+\infty \right)$.

b) Xét tam thức bậc hai – 3x² + x + 1 có: Hệ số a = – 3 < 0 và

∆ = 1² – 4 . (– 3) . 1 = 13 > 0

Suy ra tam thức này có hai nghiệm $x_1=\frac{1-\sqrt{13}}{6},x_2=\frac{1+\sqrt{13}}{6}$ 

Ta có bảng xét dấu sau:

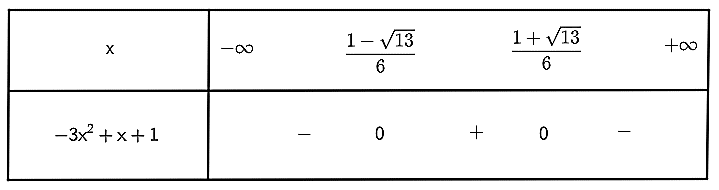
Ta thấy tam thức – 3x² + x + 1 mang dấu “+” khi $x\in \left(\frac{1-\sqrt{13}}{6};\frac{1+\sqrt{13}}{6}\right)$.

Vậy tập nghiệm của bất phương trình – 3x² + x + 1 > 0 là $\left(\frac{1-\sqrt{13}}{6};\frac{1+\sqrt{13}}{6}\right)$.

c) Xét tam thức bậc hai 4x² + 4x + 1 có hệ số a = 4 > 0 và ∆ = 4² – 4 . 4 . 1 = 0

Suy ra tam thức này có nghiệm kép là x = $-\frac{1}{2}$.

Ta có bảng xét dấu sau:

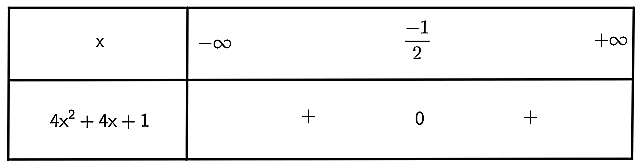
Từ bảng xét dấu ta thấy 4x² + 4x + 1 > 0 với mọi $x\ne -\frac{1}{2}$ và 4x² + 4x + 1 = 0 tại x = $-\frac{1}{2}$.

Do đó bất phương trình 4x² + 4x + 1 ≥ 0 đã cho có vô số nghiệm.

Vậy tập nghiệm của bất phương trình là $ℝ$.

d) Xét tam thức bậc hai – 16x² + 8x – 1 < 0 có hệ số a = -16 < 0 và ∆’ = 4² – (– 16) . (– 1) = 0 nên tam thức có nghiệm kép là x = $\frac{1}{4}$.

Ta có bảng xét dấu:

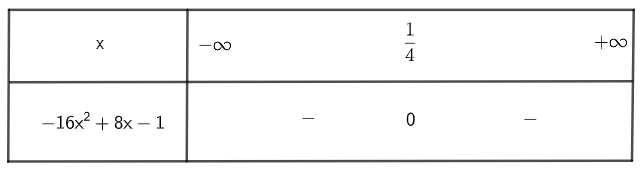
Ta thấy tam thức – 16x² + 8x – 1 < 0 với mọi $x\ne \frac{1}{4}$.

Vậy tập nghiệm của bất phương trình – 16x² + 8x – 1 < 0 là $ℝ\backslash \left\{\frac{1}{4}\right\}$.

e) Xét tam thức bậc hai 2x² + x + 3 có hệ số a = 2 > 0 và ∆ = 1² – 4 . 2 . 3 = – 23 < 0

Ta có bảng xét dấu sau:

Dựa vào bảng xét dấu ta thấy 2x² + x + 3 > 0 với mọi $x\in ℝ$.

Vậy bất phương trình 2x² + x + 3 < 0 vô nghiệm.

g) – 3x² + 4x – 5 < 0

Xét tam thức bậc hai – 3x² + 4x – 5 có hệ số a = – 3 < 0 và ∆’ = 2² – (– 3) . (– 5) = – 11 < 0.

Ta có bảng xét dấu:

Dựa vào bảng xét dấu ta thấy – 3x² + 4x – 5 < 0 với mọi $x\in ℝ$.

Vậy tập nghiệm của bất phương trình – 3x² + 4x – 5 < 0 là $ℝ$.

Bài 8 trang 61 Toán lớp 10 Tập 1: Giải các phương trình sau:

a) $\sqrt{x+2}=x$

b) $\sqrt{2x^2+3x-2}=\sqrt{x^2+x+6}$;

c) $\sqrt{2x^2+3x-1}=x+3$. 

Lời giải:

a) $\sqrt{x+2}=x$ (1)

Điều kiện: x > 0

(1) ⇔ x + 2 = x²

⇔ x² – x – 2 = 0

$\iff \left[\begin{array}{l}x=-1\left(khôngTMĐK\right)\\ x=2\left(TMĐK\right)\end{array}\right.$

Vậy nghiệm của phương trình đã cho là x = 2.

b) $\sqrt{2x^2+3x-2}=\sqrt{x^2+x+6}$ 

⇔ 2x² + 3x – 2 = x² + x + 6

⇔ 2x² – x² + 3x – x – 2 – 6 = 0

⇔ x² + 2x – 8 = 0

$\iff \left[\begin{array}{l}x=-4\\ x=2\end{array}\right.$

Thay x = -4  và x = 2 lần lượt vào bất đẳng thức 2x² + 3x – 2 ≥ 0 ta thấy cả hai giá trị đều thỏa mãn bất đẳng thức.

Vậy nghiệm của phương trình đã cho là x = 2 và x = – 4.

c) $\sqrt{2x^2+3x-1}=x+3$ (3)

Điều kiện x + 3 ≥ 0 ⇔ x ≥ – 3.

Phương trình (3) ⇔ 2x² + 3x – 1 = (x + 3)²

⇔ 2x² + 3x – 1 = x² + 6x + 9

⇔ 2x² – x² + 3x – 6x – 1 – 9 = 0

⇔ x² – 3x – 10 = 0

$\iff \left[\begin{array}{l}x=-2\\ x=5\end{array}\right.$(thỏa mãn điều kiện)

Vậy nghiệm của phương trình đã cho là x = – 2 và x = 5.

Bài 9 trang 61 Toán lớp 10 Tập 1: Một kĩ sư thiết kế đường dây điện từ vị trí A đến vị trí S và từ vị trí S đến vị trí C trên cù lao như Hình 38. Tiền công thiết kế mỗi ki-lô-mét đường dây từ A đến S và từ S đến C lần lượt là 3 triệu đồng và 5 triệu đồng. Biết tổng số tiền công là 16 triệu đồng. Tính tổng số ki-lô-mét đường dây điện đã thiết kế.

Lời giải:

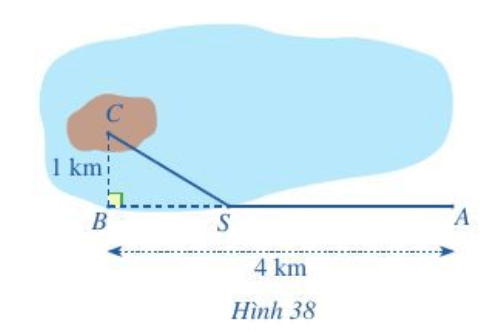
Gọi số ki-lô-mét đường dây điện từ vị trí B đến vị trí S là x (km) (x > 0).

Khi đó, ta có: SA = AB – BS = 4 - x (km) (Ta có 4 – x > 0 ⇔ x < 4)

Số tiền công thiết kế trên đoạn đường SA là: 3(4 – x) (triệu đồng)

Xét ∆CBS vuông tại B, có:

CS² = BS² + BC² (định lý Py – ta – go)

CS² = x² + 1² = x² + 1

CS = $\sqrt{x^2+1}$ (km)

Số tiền công thiết kế trên đoạn đường CS là: $5\sqrt{x^2+1}$ (triệu đồng)

Tổng số tiền công thiết kế đường dây điện trên cả quãng đường AC là:

$5\sqrt{x^2+1}+3\left(4-x\right)$ (triệu đồng)

Vì tổng số tiền công là 16 triệu đồng nên ta có phương trình:

$5\sqrt{x^2+1}+3\left(4-x\right)=16$

$\iff 5\sqrt{x^2+1}=3x+4$ (1)

Điều kiện 3x + 4 ≥ 0 ⇔ $x\ge -\frac{4}{3}$

Phương trình (1) ⇔ 25(x² + 1) = (3x + 4)²

⇔ 25x² + 25 = 9x² + 24x + 16

⇔ 16x² - 24x + 9 = 0

$\iff x=\frac{3}{4}=0,75$ (thỏa mãn điều kiện)

Do đó số ki-lô-mét đường dây từ vị trí A đến S là 4 – 0,75 = 3,25 km.

Số ki-lô-mét đường dây từ vị trí S đến C là: $\sqrt{x^2+1}=\sqrt{{\left(0,75\right)}^2+1}=1,25$ (km).

Vậy tổng số ki-lô-mét đường dây đã thiết kế là 3,25 + 1,25 = 4,5 (km).

Xem thêm lời giải bài tập SGK Toán lớp 10 Cánh Diều hay, chi tiết khác:

Bài 4: Bất phương trình bậc hai một ẩn

Bài 5: Hai dạng phương trình quy về phương trình bậc hai

Bài 1: Giá trị lượng giác của một góc từ 0 độ đến 180 độ. Định lý côsin và định lý sin trong tam giác

Bài 2: Giải tam giác. Tính diện tích tam giác

Bài 3: Khái niệm vectơ