Hai ô tô xuất phát tại cùng một điểm với vận tốc trung bình như nhau là 40 km/h từ hai vị trí A và B trên hai con đường vuông góc với nhau để đi về bến O là giao của hai con đường

Câu hỏi khởi động trang 56 Toán lớp 10 Tập 1: Hai ô tô xuất phát tại cùng một điểm với vận tốc trung bình như nhau là 40 km/h từ hai vị trí A và B trên hai con đường vuông góc với nhau để đi về bến O là giao của hai con đường. Vị trí A cách bến 8 km, vị trí B cách bến 7 km. Gọi x là thời gian hai xe bắt đầu chạy cho tới khi cách nhau 5 km (Hình 31).

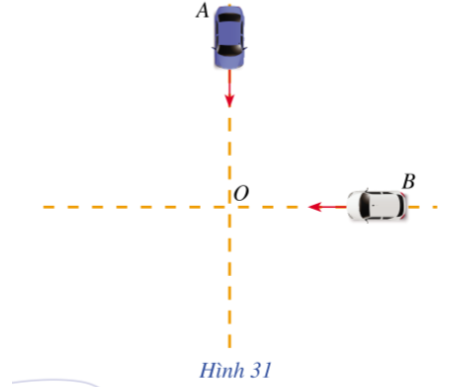
Bạn Dương xác định được x thỏa mãn phương trình $\sqrt{{\left(8-40x\right)}^2+{\left(7-40x\right)}^2}=5.$

Làm thế nào để tìm được giá trị của x?

Trả lời

Sau bài học này ta sẽ giải quyết bài toán này như sau:

Để tìm được giá trị của x, ta cần giải phương trình $\sqrt{{\left(8-40x\right)}^2+{\left(7-40x\right)}^2}=5$ (1).

Điều kiện xác định: (8 – 40x)² + (7 – 40x)² ≥ 0.

Vì (8 – 40x)² ≥ 0 và (7 – 40x)² ≥ 0 với mọi x nên (8 – 40x)² + (7 – 40x)² ≥ 0 với mọi x.

Bình phương hai vế ta được: (8 – 40x)² + (7 – 40x)² = 25

⇔ 1 600x² – 640x + 64 + 1 600x² – 560x + 49 = 25

⇔ 3 200x² – 1 200x + 88 = 0

⇔ 400x² – 150x + 11 = 0

$\iff \left[\begin{array}{l}x=0,1\\ x=0,275\end{array}\right.$(thỏa mãn điều kiện)

Vậy có hai giá trị của x: x = 0,1 hoặc x = 0,275 nghĩa là có hai thời điểm để hai xe cách nhau 5km.

Xem thêm lời giải bài tập SGK Toán lớp 10 Cánh Diều hay, chi tiết khác:

Bài 3: Dấu của tam thức bậc hai

Bài 4: Bất phương trình bậc hai một ẩn

Bài 5: Hai dạng phương trình quy về phương trình bậc hai

Bài tập cuối chương 3

Bài 1: Giá trị lượng giác của một góc từ 0 độ đến 180 độ. Định lý côsin và định lý sin trong tam giác

Bài 2: Giải tam giác. Tính diện tích tam giác