Giải SGK Toán 10 (Kết nối tri thức) Bài 20: Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách

Giải Toán 10 Bài 20: Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách

Mở đầu

Mở đầu trang 36 Toán 10 Tập 2: Trong mặt phẳng tọa độ, mỗi đường thẳng đều có đối tượng đại số tương ứng, gọi là phương trình của nó. Vậy các yếu tố liên quan tới đường thẳng được thể hiện như thế nào qua phương trình tương ứng?

Lời giải:

Để biết các yếu tố liên quan tới đường thẳng được thể hiện qua phương trình tương ứng như thế nào ta cùng tìm hiểu qua bài học 20. 

1. Vị trí tương đối giữa hai đường thẳng

HĐ1 trang 36 Toán 10 Tập 2: Trong mặt phẳng tọa độ, cho hai đường thẳng 

∆₁: x – 2y + 3 = 0,

∆₂: 3x – y – 1 = 0.

a) Điểm M(1; 2) có thuộc cả hai đường thẳng nói trên hay không? 

b) Giải hệ $\left\{\begin{array}{l}x-2y+3=0\\ 3x-y-1=0\end{array}\right.$. 

c) Chỉ ra mối quan hệ giữa tọa độ giao điểm của ∆₁ và ∆₂ với nghiệm của hệ phương trình trên. 

Lời giải:

a) Thay tọa độ điểm M(1; 2) vào phương trình ∆₁ ta được: 

1 – 2 . 2 + 3 = 0 ⇔ 0 = 0 (luôn đúng).

Do đó điểm M thuộc ∆₁. 

Thay tọa độ điểm M(1; 2) vào phương trình ∆₂ ta được: 

3 . 1 – 2 – 1 = 0 ⇔ 0 = 0 (luôn đúng). 

Do đó điểm M thuộc ∆₂. 

Vậy M thuộc cả hai đường thẳng ∆₁ và ∆_2­. 

b) Ta có: $\left\{\begin{array}{l}x-2y+3=0\\ 3x-y-1=0\end{array}\right.\iff \left\{\begin{array}{l}x-2y+3=0\left(1\right)\\ 6x-2y-2=0\left(2\right)\end{array}\right.$

Lấy (2) trừ (1) theo vế ta được: 5x – 5 = 0 ⇔ x = 1.

Thay x = 1 vào (1) ta được: 1 – 2y + 3 = 0 ⇔ 2y = 4 ⇔ y = 2. 

Vậy nghiệm của hệ đã cho là (x; y) = (1; 2). 

c) Theo câu a, điểm M(1; 2) thuộc cả hai đường thẳng ∆₁ và ∆₂ nên M là giao điểm của hai đường thẳng này. 

Do đó ta thấy tọa độ giao điểm của ∆₁ và ∆₂ giống với nghiệm của hệ phương trình ở câu b. 

Luyện tập 1 trang 37 Toán 10 Tập 2: Xét vị trí tương đối giữa các cặp đường thẳng sau: 

a) ∆₁: x + 4y – 3 = 0 và ∆₂: x – 4y – 3 = 0; 

b) ∆₁: x + 2y –$\sqrt{5}$ = 0 và ∆₂: 2x + 4y – $3\sqrt{5}$= 0.

Lời giải:

a) Xét hệ $\left\{\begin{array}{l}x+4y-3=0\left(1\right)\\ x-4y-3=0\left(2\right)\end{array}\right.$

Lấy (1) cộng vế theo vế với (2) ta được: 2x – 6 = 0 ⇔ x = 3. 

Thay x = 3 vào (1) ta được: 3 + 4y – 3 = 0 ⇔ 4y = 0 ⇔ y = 0. 

Do đó hệ phương trình trên có nghiệm duy nhất (x; y) = (3; 0). 

Vậy hai đường thẳng ∆₁ và ∆₂ cắt nhau tại điểm M(3; 0). 

b) Đường thẳng ∆₁: x + 2y –$\sqrt{5}$= 0 có vectơ pháp tuyến là ${\overrightarrow{n}}_1=\left(1;2\right)$. 

Đường thẳng ∆₂: 2x + 4y – $3\sqrt{5}$= 0 có vectơ pháp tuyến là ${\overrightarrow{n}}_2=\left(2;4\right)$.

Ta thấy: ${\overrightarrow{n}}_2=2{\overrightarrow{n}}_1$ nên hai vectơ này cùng phương. 

Do đó hai đường thẳng ∆₁ và ∆₂ song song hoặc trùng nhau. 

Mặt khác, ta lại có điểm A($\sqrt{5}$; 0) thuộc đường thẳng ∆₁ nhưng không thuộc đường thẳng ∆₂ nên hai đường thẳng này không trùng nhau. 

Vậy hai đường thẳng ∆₁ và ∆₂ song song với nhau. 

2. Góc giữa hai đường thẳng

HĐ2 trang 37 Toán 10 Tập 2: Hai đường thẳng ∆₁ và ∆₂ cắt nhau tạo thành bốn góc (H.7.6). Các số đo của bốn góc đó có mối quan hệ gì với nhau?

Lời giải:

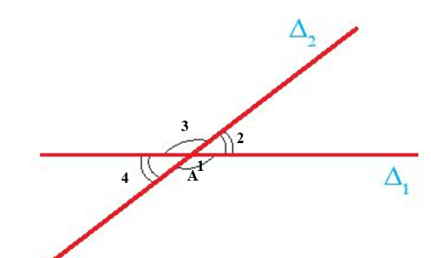
Hai đường thẳng cắt nhau tạo thành bốn góc, trong đó có hai cặp góc đối đỉnh với nhau. Hai góc đối đỉnh thì có số đo bằng nhau. 

Hai đường thẳng ∆₁ và ∆₂ cắt nhau tại A. Khi đó ta có:

+) ${\widehat{A}}_1={\widehat{A}}_3$ (2 góc đối đỉnh);

+) ${\widehat{A}}_2={\widehat{A}}_4$ (2 góc đối đỉnh).

HĐ3 trang 38 Toán 10 Tập 2: Cho hai đường thẳng cắt nhau ∆₁, ∆₂ tương ứng có các vectơ pháp tuyến ${\overrightarrow{n}}_1,{\overrightarrow{n}}_2$. Gọi φ là góc giữa hai đường thẳng đó (H.7.7). Nêu mối quan hệ giữa: 

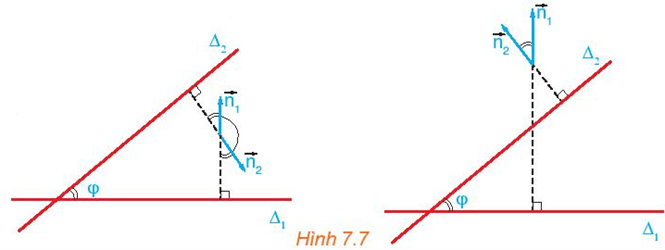
a) góc φ và góc $({\overrightarrow{n}}_1,{\overrightarrow{n}}_2\text{)}$;

b) cosφ và cos$({\overrightarrow{n}}_1,{\overrightarrow{n}}_2\text{)}$.

Lời giải:

a) Quan sát Hình 7.7, ta thấy góc giữa hai đường thẳng ∆₁ và ∆₂ là góc φ, góc này bằng hoặc bù với góc giữa hai vectơ ${\overrightarrow{n}}_1$ và ${\overrightarrow{n}}_2$. 

b) 

+) Với trường hợp góc φ và góc$({\overrightarrow{n}}_1,{\overrightarrow{n}}_2\text{)}$ bằng nhau thì ta có: cosφ = cos$({\overrightarrow{n}}_1,{\overrightarrow{n}}_2\text{)}$;

+) Với trường hợp góc φ và góc$({\overrightarrow{n}}_1,{\overrightarrow{n}}_2\text{)}$ bù nhau thì ta có: cosφ = – cos$({\overrightarrow{n}}_1,{\overrightarrow{n}}_2\text{)}$.

Luyện tập 2 trang 38 Toán 10 Tập 2: Tính góc giữa hai đường thẳng 

∆₁: x + 3y + 2 = 0 và ∆₂: y = 3x + 1. 

Lời giải:

Vectơ pháp tuyến của đường thẳng ∆₁ là ${\overrightarrow{n}}_1=\left(1;3\right)$.

Ta có: y = 3x + 1 ⇔ 3x – y + 1 = 0 hay ∆₂: 3x – y + 1 = 0, do đó vectơ pháp tuyến của đường thẳng ∆₂ là ${\overrightarrow{n}}_2=\left(3;-1\right)$. 

Gọi φ là góc giữa hai đường thẳng ∆₁ và ∆₂. Ta có: 

cosφ = $\left|\cos \left({\overrightarrow{n}}_1,{\overrightarrow{n}}_2\right)\right|=\frac{\left|{\overrightarrow{n}}_1.{\overrightarrow{n}}_2\right|}{\left|{\overrightarrow{n}}_1\right|.\left|{\overrightarrow{n}}_2\right|}=\frac{\left|1.3+3.\left(-1\right)\right|}{\sqrt{1^2+3^2}.\sqrt{3^2+{\left(-1\right)}^2}}=0$. 

Do đó hai đường thẳng ∆₁ và ∆₂ vuông góc và φ = 90°. 

Luyện tập 3 trang 39 Toán 10 Tập 2: Tính góc giữa hai đường thẳng ${\Delta }_1:\left\{\begin{array}{l}x=2+t\\ y=1-2t\end{array}\right.$và ${\Delta }_2:\left\{\begin{array}{l}x=1+t^{\text{'}}\\ y=5+3t^{\text{'}}\end{array}\right.$. 

Lời giải:

Vectơ chỉ phương của đường thẳng ∆₁ là ${\overrightarrow{u}}_1=\left(1;-2\right)$, của ∆₂ là ${\overrightarrow{u}}_2=\left(1;3\right)$. 

Suy ra vectơ pháp tuyến của ∆₁ là ${\overrightarrow{n}}_1=\left(2;1\right)$, của ∆­₂ là ${\overrightarrow{n}}_2=\left(3;-1\right)$. 

Gọi φ là góc giữa hai đường thẳng ∆₁ và ∆₂. Ta có: 

cosφ = $\left|\cos \left({\overrightarrow{n}}_1,{\overrightarrow{n}}_2\right)\right|=\frac{\left|{\overrightarrow{n}}_1.{\overrightarrow{n}}_2\right|}{\left|{\overrightarrow{n}}_1\right|.\left|{\overrightarrow{n}}_2\right|}=\frac{\left|2.3+1.\left(-1\right)\right|}{\sqrt{2^2+1^2}.\sqrt{3^2+{\left(-1\right)}^2}}=\frac{5}{\sqrt{5}.\sqrt{10}}=\frac{\sqrt{2}}{2}$. 

Do đó, góc giữa ∆₁ và ∆₂ là φ = 45°. 

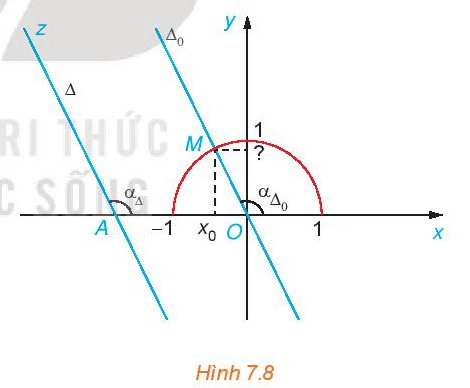
Luyện tập 4 trang 39 Toán 10 Tập 2: Cho đường thẳng ∆: y = ax + b với a ≠ 0. 

a) Chứng minh rằng ∆ cắt trục hoành. 

b) Lập phương trình đường thẳng ∆₀ đi qua O(0; 0) và song song (hoặc trùng) với ∆. 

c) Hãy chỉ ra mối quan hệ giữa α_∆ và α_∆0. 

d) Gọi M là giao điểm của ∆₀ với nửa đường tròn đơn vị và x₀ là hoành độ của M. Tính tung độ của M theo x₀ và a. Từ đó, chứng minh rằng tanα_∆ = a. 

Lời giải:

a) Phương trình trục hoành Ox: y = 0. 

Xét hệ $\left\{\begin{array}{l}y=0\\ y=ax+b\end{array}\right.$. 

Khi đó ta có: ax + b = 0 ⇔ x = $-\frac{b}{a}$(do a ≠ 0). 

Do đó hệ trên có nghiệm duy nhất $\left(-\frac{b}{a};0\right)$ nên ∆ và trục hoành cắt nhau tại giao điểm có tọa độ $\left(-\frac{b}{a};0\right)$. 

b) Đường thẳng ∆ có vectơ pháp tuyến là $\overrightarrow{n}=\left(a;-1\right)$. 

Do đường thẳng ∆₀ song song hoặc trùng với ∆ nên ta chọn vectơ $\overrightarrow{n}$ là một vectơ pháp tuyến của ∆₀. 

Đường thẳng ∆₀ đi qua điểm O(0; 0) và nhận $\overrightarrow{n}=\left(a;-1\right)$ làm vectơ pháp tuyến. 

Khi đó phương trình đường thẳng ∆₀ là: a(x – 0) – (y – 0) = 0 hay ax – y = 0 hay y = ax. 

c) Khi ∆ và ∆₀ trùng nhau thì α_∆ và α_∆0 trùng nhau nên α_∆ = α_∆0. 

Khi ∆ và ∆₀ song song thì α_∆ = α_∆0 (do hai góc ở vị trí đồng vị). 

Vậy α_∆ = α_∆0.

d) Vì M thuộc đường thẳng ∆₀ nên tọa độ điểm M thỏa mãn phương trình đường thẳng ∆₀ nên khi có hoành độ x₀ thì tung độ của M là y₀ = ax₀. 

Ta có tanα_∆0 = tan∠xOM = $\frac{y_0}{x_0}=\frac{a{x}_0}{x_0}=a$ (theo định nghĩa giá trị lượng giác)

Do α_∆ = α_∆0 nên tanα_∆ = tanα_∆0 = a. 

Vậy tanα_∆ = a. 

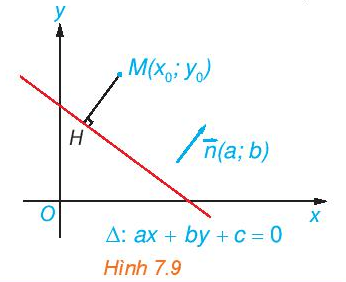
3. Khoảng cách từ một điểm đến một đường thẳng

HĐ4 trang 40 Toán 10 Tập 2: Cho điểm M(x₀; y₀) và đường thẳng ∆: ax + by + c = 0 có vectơ pháp tuyến $\overrightarrow{n}\left(a;b\right)$. Gọi H là hình chiếu vuông góc của M trên ∆ (H.7.9). 

a) Chứng minh rằng $\left|\overrightarrow{n}.\overrightarrow{HM}\right|=\sqrt{a^2+b^2}.HM$.

b) Giả sử H có tọa độ (x₁; y₁). Chứng minh rằng: $\overrightarrow{n}.\overrightarrow{HM}$= a(x₀ – x₁) + b(y₀ – y₁) = ax₀ + by₀ + c. 

c) Chứng minh rằng $HM=\frac{\left|a{x}_0+b{y}_0+c\right|}{\sqrt{a^2+b^2}}$. 

Lời giải:

a) Do H là hình chiếu của M lên ∆ nên MH ⊥ ∆.

Vectơ $\overrightarrow{n}$ là vectơ pháp tuyến của ∆ nên giá của vectơ $\overrightarrow{n}$ vuông góc với ∆. 

Khi đó đường thẳng MH song song hoặc trùng với giá của vectơ $\overrightarrow{n}$ nên hai vectơ $\overrightarrow{HM}$ và $\overrightarrow{n}$cùng phương. 

Do đó hai vectơ $\overrightarrow{HM}$ và $\overrightarrow{n}$ cùng hướng hoặc ngược hướng.

+) Nếu hai vectơ $\overrightarrow{HM}$ và $\overrightarrow{n}$ cùng hướng thì $\overrightarrow{n}.\overrightarrow{HM}=\left|\overrightarrow{n}\right|.\left|\overrightarrow{HM}\right|=\sqrt{a^2+b^2}.HM$.

+) Nếu hai vectơ $\overrightarrow{HM}$ và $\overrightarrow{n}$ ngược hướng thì $\overrightarrow{n}.\overrightarrow{HM}=-\left|\overrightarrow{n}\right|.\left|\overrightarrow{HM}\right|=-\sqrt{a^2+b^2}.HM$.

Vậy $\left|\overrightarrow{n}.\overrightarrow{HM}\right|=\sqrt{a^2+b^2}.HM$. 

b) Vì H thuộc ∆ nên tọa độ của H thỏa mãn phương trình ∆, thay tọa độ của H vào phương trình ∆ ta được: ax₁ + by₁ + c = 0 ⇔ c = – ax₁ – by₁           (1). 

Ta lại có: $\overrightarrow{HM}=\left(x_0-x_1;y_0-y_1\right)$.

Suy ra: $\overrightarrow{n}.\overrightarrow{HM}=a\left(x_0-x_1\right)+b\left(y_0-y_1\right)$ = ax₀ + by₀ – ax₁ – by₁             (2). 

Từ (1) và (2) suy ra : $\overrightarrow{n}.\overrightarrow{HM}=a\left(x_0-x_1\right)+b\left(y_0-y_1\right)$ = ax₀ + by₀ + c. 

c) Theo câu a) ta có: $\left|\overrightarrow{n}.\overrightarrow{HM}\right|=\sqrt{a^2+b^2}.HM$. 

Theo câu b) ta có: $\overrightarrow{n}.\overrightarrow{HM}$ = ax₀ + by₀ + c. 

Suy ra: |ax₀ + by₀ + c| = $\sqrt{a^2+b^2}.HM$.

Vậy $HM=\frac{\left|a{x}_0+b{y}_0+c\right|}{\sqrt{a^2+b^2}}$.

Trải nghiệm trang 40 Toán 10 Tập 2: Đo trực tiếp khoảng cách từ điểm M đến đường thẳng ∆ (H.7.10) và giải thích vì sao kết quả đo đạc đó phù hợp với kết quả tính toán trong lời giải Ví dụ 4. 

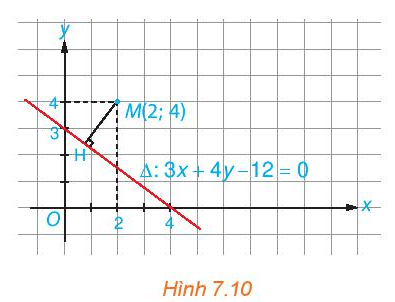
Lời giải:

Khoảng cách từ M đến đường thẳng ∆ là độ dài đoạn MH. 

Dùng thước ta đo được MH có độ dài bằng 2 ô vuông trên mặt phẳng tọa độ Oxy nên MH = 2. 

Kết quả này hoàn toàn phù hợp với kết quả tính được trong lời giải của Ví dụ 4 vì điểm M ở đây có tọa độ trùng với điểm M của Ví dụ 4 và đường thẳng Δ có phương trình trùng với phương trình trong Ví dụ 4.

Luyện tập 5 trang 40 Toán 10 Tập 2: Tính khoảng cách từ điểm M(1; 2) đến đường thẳng $\Delta :\left\{\begin{array}{l}x=5+3t\\ y=-5-4t\end{array}\right.$. 

Lời giải:

Đường thẳng $\Delta :\left\{\begin{array}{l}x=5+3t\\ y=-5-4t\end{array}\right.$đi qua điểm A(5; – 5) và có một vectơ chỉ phương là $\overrightarrow{u}=\left(3;-4\right)$, suy ra ∆ có vectơ pháp tuyến là $\overrightarrow{n}=\left(4;3\right)$. 

Do đó, phương trình tổng quát của ∆ là: 4(x – 5) + 3(y + 5) = 0 hay 4x + 3y – 5 = 0. 

Áp dụng công thức tính khoảng cách từ điểm M đến đường thẳng ∆, ta có: 

d(M, ∆) = $\frac{\left|4.1+3.2-5\right|}{\sqrt{4^2+3^2}}=\frac{5}{5}=1$. 

Vậy khoảng cách từ điểm M đến đường thẳng ∆ là 1. 

Vận dụng trang 41 Toán 10 Tập 2: Nhân dịp nghỉ hè, Nam về quê ở với ông bà nội. Nhà ông bà nội có một ao cá có dạng hình chữ nhật ABCD với chiều dài AD = 15 m, chiều rộng AB = 12 m. Phần tam giác DEF là nơi ông bà nuôi vịt, AE = 5 m, CF = 6 m (H.7.11). 

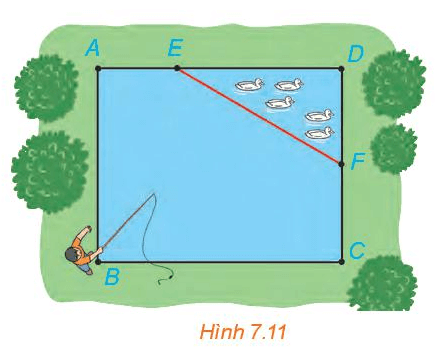
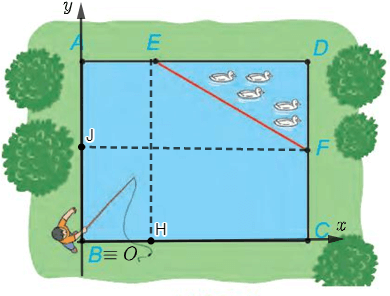
a) Chọn hệ trục tọa độ Oxy, có điểm O trùng với điểm B, các tia Ox, Oy tương ứng trùng với các tia BC, BA. Chọn 1 đơn vị độ dài trên mặt phẳng tọa độ tương ứng với 1 m trong thực tế. Hãy xác định tọa độ của các điểm A, B, C, D, E, F và viết phương trình đường thẳng EF. 

b) Nam đứng ở vị trí B câu cá và có thể quăng lưỡi câu xa 10,7 m. Hỏi lưỡi câu có thể rơi vào nơi nuôi vịt hay không ? 

Lời giải:

a) Đặt hệ trục tọa độ như hình vẽ sau: 

Vì B trùng với gốc tọa độ O nên B có tọa độ là (0; 0). 

Vì ABCD là hình chữ nhật nên CD = AB = 12 m, BC = AD = 15 m. 

Điểm A thuộc trục Oy và có AO = AB = 12 m nên A có tọa độ là (0; 12). 

Điểm C thuộc trục Ox và có CO = CB = 15 m nên C có tọa độ là (15; 0). 

Ta có: DC ⊥ Ox (do DC ⊥ BC), DA ⊥ Oy (do DA ⊥ AB) và DC = 12 m, DA = 15 m nên điểm D có tọa độ là (15; 12). 

Từ E kẻ EH vuông góc với BC, H thuộc BC nên EH = AB = 12 m, lại có AE = 5 m, do đó điểm E có tọa độ là (5; 12).

Từ F kẻ FJ vuông góc với AB, J thuộc AB nên FJ = AD = 15 m, lại có CF = 6 m, do đó điểm F có tọa độ là (15; 6). 

Vậy A(0; 12), B(0; 0), C(15; 0), D(15; 12), E(5; 12), F(15; 6). 

Ta có: $\overrightarrow{EF}=\left(15-5;6-12\right)=\left(10;-6\right)$. 

Chọn vectơ $\overrightarrow{u}=\frac{1}{2}\overrightarrow{EF}=\left(5;-3\right)$ làm vectơ chỉ phương của đường thẳng EF thì vectơ pháp tuyến của đường thẳng EF là $\overrightarrow{n}=\left(3;5\right)$. 

Đường thẳng EF đi qua điểm E(5; 12) và có một vectơ pháp tuyến là $\overrightarrow{n}=\left(3;5\right)$, do đó phương trình đường thẳng EF là: 3(x – 5) + 5(y – 12) = 0 hay 3x + 5y – 75 = 0. 

b) Áp dụng công thức tính khoảng cách, ta có khoảng cách từ B đến EF là: 

$d\left(B,EF\right)=\frac{\left|3.0+5.0-75\right|}{\sqrt{3^2+5^2}}=\frac{75}{\sqrt{34}}$≈ 12,9 m. 

Khoảng cách từ B đến EF là đường ngắn nhất từ B nơi Nam đứng đến EF, lưỡi câu có thể quăng xa 10,7 m và 10,7 m < 12,9 m nên lưỡi câu không thể rơi vào vị trí nuôi vịt. 

Bài tập

Bài 7.7 trang 41 Toán 10 Tập 2: Xét vị trí tương đối giữa các cặp đường thẳng sau: 

a) ∆₁: $3\sqrt{2}x+\sqrt{2}y-\sqrt{3}=0$và ∆₂: 6x + 2y $-\sqrt{6}$= 0. 

b) d₁: x $-\sqrt{3}y$+ 2 = 0 và d₂: $\sqrt{3}x$– 3y + 2 = 0. 

c) m₁: x – 2y + 1 = 0 và m₂: 3x + y – 2 = 0. 

Lời giải:

a) Đường thẳng ∆₁: $3\sqrt{2}x+\sqrt{2}y-\sqrt{3}=0$có vectơ pháp tuyến là ${\overrightarrow{n}}_1=\left(3\sqrt{2};\sqrt{2}\right)$. 

Đường thẳng ∆₂: 6x + 2y$-\sqrt{6}$ = 0 có vectơ pháp tuyến là ${\overrightarrow{n}}_2=\left(6;2\right)$. 

Ta có: ${\overrightarrow{n}}_1=\frac{\sqrt{2}}{2}{\overrightarrow{n}}_2$ nên hai vectơ ${\overrightarrow{n}}_1$ và ${\overrightarrow{n}}_2$ cùng phương, do đó hai đường thẳng ∆₁ và ∆₂ song song hoặc trùng nhau. 

Mặt khác, điểm A$\left(0;\frac{\sqrt{6}}{2}\right)$ vừa thuộc ∆₁ vừa thuộc ∆₂. 

Vậy hai đường thẳng ∆₁ và ∆₂ trùng nhau. 

b) Vectơ pháp tuyến của đường thẳng d₁: x$-\sqrt{3}y$ + 2 = 0 là $\overrightarrow{n_1}=\left(1;-\sqrt{3}\right)$ và của d₂: $\sqrt{3}$x – 3y + 2 = 0 là $\overrightarrow{n_2}=\left(\sqrt{3};-3\right)$. 

Ta có: $\overrightarrow{n_2}=\sqrt{3}\overrightarrow{n_1}$ nên hai vectơ ${\overrightarrow{n}}_1$ và ${\overrightarrow{n}}_2$ cùng phương, do đó hai đường thẳng d₁ và d₂ song song hoặc trùng nhau. 

Mặt khác, điểm B(– 2; 0) thuộc d₁ nhưng không thuộc d₂. 

Vậy hai đường thẳng d₁ và d₂ song song với nhau.

c) Xét hệ phương trình $\left\{\begin{array}{l}x-2y+1=0\\ 3x+y-2=0\end{array}\right.\iff \left\{\begin{array}{l}3x-6y+3=0\left(1\right)\\ 3x+y-2=0\left(2\right)\end{array}\right.$.

Lấy (2) trừ vế theo vế cho (1) ta được: 7y – 5 = 0 $\iff y=\frac{5}{7}$.

Thay vào (1) ta được: $3x-6.\frac{5}{7}+3=0\iff x=\frac{3}{7}$. 

Do đó hệ trên có nghiệm duy nhất $\left(\frac{3}{7};\frac{5}{7}\right)$. 

Vậy hai đường thẳng m₁ và m₂ cắt nhau tại điểm có tọa độ $\left(\frac{3}{7};\frac{5}{7}\right)$.

Bài 7.8 trang 41 Toán 10 Tập 2: Tính góc giữa các cặp đường thẳng sau: 

a) ∆₁:$\sqrt{3}x$ + y – 4 = 0 và ∆₂: x +$\sqrt{3}y$ + 3 = 0; 

b) d₁: $\left\{\begin{array}{l}x=-1+2t\\ y=3+4t\end{array}\right.$và d₂: $\left\{\begin{array}{l}x=3+s\\ y=1-3s\end{array}\right.$           (t, s là các tham số). 

Lời giải:

a) Vectơ pháp tuyến của đường thẳng ∆₁: $\sqrt{3}x$+ y – 4 = 0 là $\overrightarrow{n_1}=\left(\sqrt{3};1\right)$ và của ∆₂: x +$\sqrt{3}y$ + 3 = 0 là $\overrightarrow{n_2}=\left(1;\sqrt{3}\right)$. 

Gọi φ là góc giữa hai đường thẳng ∆₁ và ∆₂. Ta có: 

cosφ = $\left|\cos \left(\overrightarrow{n_1},\overrightarrow{n_2}\right)\right|=\frac{\left|\overrightarrow{n_1}.\overrightarrow{n_2}\right|}{\left|\overrightarrow{n_1}\right|.\left|\overrightarrow{n_2}\right|}=\frac{\left|\sqrt{3}.1+1.\sqrt{3}\right|}{\sqrt{{\left(\sqrt{3}\right)}^2+1^2}.\sqrt{1^2+{\left(\sqrt{3}\right)}^2}}=\frac{2\sqrt{3}}{2.2}=\frac{\sqrt{3}}{2}$. 

Do đó, góc giữa ∆₁ và ∆₂ là φ = 30°.

b) Vectơ chỉ phương của đường thẳng d₁ là $\overrightarrow{u_1}=\left(2;4\right)$, của đường thẳng d₂ là $\overrightarrow{u_2}=\left(1;-3\right)$. 

Suy ra vectơ pháp tuyến của đường thẳng d₁ là $\overrightarrow{n_1}=\left(4;-2\right)$, của đường thẳng d₂ là $\overrightarrow{n_2}=\left(3;1\right)$. 

Gọi α là góc giữa hai đường thẳng d₁ và d₂. Ta có: 

cosα = $\left|\cos \left(\overrightarrow{n_1},\overrightarrow{n_2}\right)\right|=\frac{\left|\overrightarrow{n_1}.\overrightarrow{n_2}\right|}{\left|\overrightarrow{n_1}\right|.\left|\overrightarrow{n_2}\right|}=\frac{\left|4.3+\left(-2\right).1\right|}{\sqrt{4^2+{\left(-2\right)}^2}.\sqrt{3^2+1^2}}=\frac{10}{\sqrt{20}.\sqrt{10}}=\frac{\sqrt{2}}{2}$. 

Do đó, góc giữa d₁ và d₂ là α = 45°.

Bài 7.9 trang 41 Toán 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho điểm A(0; – 2) và đường thẳng ∆: x + y – 4 = 0.

a) Tính khoảng cách từ điểm A đến đường thẳng ∆. 

b) Viết phương trình đường thẳng a đi qua điểm M(– 1; 0) và song song với ∆. 

c) Viết phương trình đường thẳng b đi qua điểm N(0; 3) và vuông góc với ∆. 

Lời giải:

a) Áp dụng công thức tính khoảng cách, ta có khoảng cách từ điểm A đến đường thẳng ∆ là: d(A, ∆) = $\frac{\left|0+\left(-2\right)-4\right|}{\sqrt{1^2+1^2}}=\frac{6}{\sqrt{2}}=3\sqrt{2}$. 

Vậy khoảng cách từ điểm A đến đường thẳng ∆ là $3\sqrt{2}$. 

b) Đường thẳng ∆ có vectơ pháp tuyến là $\overrightarrow{n_{\Delta }}=\left(1;1\right)$. 

Do a // ∆, nên vectơ pháp tuyến của a là $\overrightarrow{n_a}=\overrightarrow{n_{\Delta }}=\left(1;1\right)$. 

Đường thẳng a đi qua điểm M(– 1; 0) và có vectơ pháp tuyến là $\overrightarrow{n_a}=\left(1;1\right)$, do đó phương trình đường thẳng a là: 1(x + 1) + 1(y – 0) = 0 hay x + y + 1 = 0. 

c) Đường thẳng ∆ có vectơ chỉ phương là $\overrightarrow{u_{\Delta }}=\left(1;-1\right)$. 

Do b ⊥ ∆, nên vectơ pháp tuyến của b là $\overrightarrow{n_b}=\overrightarrow{u_{\Delta }}=\left(1;-1\right)$.

Đường thẳng b đi qua điểm N(0; 3) và có vectơ pháp tuyến là $\overrightarrow{n_b}=\left(1;-1\right)$, do đó phương trình đường thẳng b là: 1(x – 0) – 1(y – 3) = 0 hay x – y + 3 = 0. 

Bài 7.10 trang 41 Toán 10 Tập 2: Trong mặt phẳng tọa độ, cho tam giác ABC có A(1; 0), B(3; 2) và C(– 2; – 1). 

a) Tính độ dài đường cao kẻ từ đỉnh A của tam giác ABC. 

b) Tính diện tích tam giác ABC. 

Lời giải:

a) Độ dài đường cao kẻ từ đỉnh của tam giác ABC chính là khoảng cách từ điểm A đến đường thẳng BC. 

Ta có: $\overrightarrow{BC}=\left(-2-3;-1-2\right)=\left(-5;-3\right)$. 

Chọn vectơ chỉ phương của đường thẳng BC là $\overrightarrow{u}=-\overrightarrow{BC}=\left(5;3\right)$. 

Suy ra vectơ pháp tuyến của đường thẳng BC là $\overrightarrow{n}=\left(3;-5\right)$. 

Đường thẳng BC đi qua điểm B(3; 2) và có vectơ pháp tuyến $\overrightarrow{n}=\left(3;-5\right)$, do đó phương trình đường thẳng BC là: 3(x – 3) – 5(y – 2) = 0 hay 3x – 5y + 1 = 0. 

Khi đó khoảng cách từ A đến BC là: 

d(A, BC) = $\frac{\left|3.1-5.0+1\right|}{\sqrt{3^2+5^2}}=\frac{4}{\sqrt{34}}=\frac{2\sqrt{34}}{17}$. 

Vậy độ dài đường cao kẻ từ đỉnh A của tam giác ABC là h = $\frac{2\sqrt{34}}{17}$. 

b) Ta có: BC = $\left|\overrightarrow{BC}\right|=\sqrt{{\left(-5\right)}^2+{\left(-3\right)}^2}=\sqrt{34}$. 

Diện tích tam giác ABC là: 

S = $\frac{1}{2}h.BC=\frac{1}{2}.\frac{2\sqrt{34}}{17}.\sqrt{34}=2$(đvdt). 

Vậy diện tích tam giác ABC là 2 đvdt.

Bài 7.11 trang 41 Toán 10 Tập 2: Chứng minh rằng hai đường thẳng d: y = ax + b (a ≠ 0) và d': y = a'x + b' (a' ≠ 0) vuông góc với nhau khi và chỉ khi aa' = – 1. 

Lời giải:

Ta có: y = ax + b ⇔ ax – y + b = 0 hay d: ax – y + b = 0 nên vectơ pháp tuyến của đường thẳng d là $\overrightarrow{n}=\left(a;-1\right)$. 

Lại có: y = a'x + b' ⇔ a'x – y + b' = 0 hay d': a'x – y + b' = 0 nên vectơ pháp tuyến của đường thẳng d' là $\overrightarrow{n^{\text{'}}}=\left(a\text{'};-1\right)$. 

Hai đường thẳng d và d' vuông góc với nhau khi $\overrightarrow{n}\perp \overrightarrow{n^{\text{'}}}\iff \overrightarrow{n}.\overrightarrow{n^{\text{'}}}=0\iff a.a\text{'}+\left(-1\right).\left(-1\right)=0$ 

$\iff a.a\text{'}+1=0\iff a.a\text{'}=-1$. 

Vậy d ⊥ d' ⇔ aa' = – 1. 

Bài 7.12 trang 41 Toán 10 Tập 2: Trong mặt phẳng tọa độ, một tín hiệu âm thanh phát đi từ một vị trí và được ba thiết bị ghi tín hiệu đặt tại ba vị trí O(0; 0), A(1; 0), B(1; 3) nhận được cùng một thời điểm. Hãy xác định vị trí phát tín hiệu âm thanh. 

Lời giải:

Gọi H(a; b) là vị trí tín hiệu âm thanh phát đi. 

Vì ba thiết bị ghi tín hiệu đặt tại ba vị trí O(0; 0), A(1; 0), B(1; 3) nhận tín hiệu từ H phát đi tại cùng một thời điểm nên HO = HA = HB. 

Ta có: $\overrightarrow{HO}=\left(-a;-b\right)$, $\overrightarrow{HA}=\left(1-a;-b\right)$, $\overrightarrow{HC}=\left(1-a;3-b\right)$. 

Do đó: $HO=\sqrt{{\left(-a\right)}^2+\left(-b^2\right)}=\sqrt{a^2+b^2}$, $HA=\sqrt{{\left(1-a\right)}^2+{\left(-b\right)}^2}=\sqrt{{\left(a-1\right)}^2+b^2}$, $HC=\sqrt{{\left(1-a\right)}^2+{\left(3-b\right)}^2}=\sqrt{{\left(a-1\right)}^2+{\left(b-3\right)}^2}$. 

Vì HO = HA nên $\sqrt{a^2+b^2}=\sqrt{{\left(a-1\right)}^2+b^2}$ $\Rightarrow a^2+b^2={\left(a-1\right)}^2+b^2$

⇔ a² = a² – 2a + 1 ⇔ 2a = 1 ⇔ a = $\frac{1}{2}$. 

Vì HA = HB nên $\sqrt{{\left(a-1\right)}^2+b^2}=\sqrt{{\left(a-1\right)}^2+{\left(b-3\right)}^2}$

$\Rightarrow {\left(a-1\right)}^2+b^2={\left(a-1\right)}^2+{\left(b-3\right)}^2$

⇔ b² = b² – 6b + 9 ⇔ 6b = 9 ⇔ b = $\frac{3}{2}$. 

Thay a = $\frac{1}{2}$ và b = $\frac{3}{2}$ vào các phương trình ta thấy đều thỏa mãn. 

Vậy vị trí phát tín hiệu âm thanh là tại điểm H có tọa độ $\left(\frac{1}{2};\frac{3}{2}\right)$. 

Xem thêm lời giải bài tập SGK Toán lớp 10 Kết nối tri thức hay, chi tiết khác:

Bài 21: Đường tròn trong mặt phẳng tọa độ

Bài 22: Ba đường conic

Bài tập cuối chương 7 trang 58, 59

Bài 23: Quy tắc đếm

Bài 24: Hoán vị, chỉnh hợp và tổ hợp