Giải SBT Toán 7 (Cánh diều) Bài 1: Tổng các góc của một tam giác

Tổng quan

Hỏi đáp (10)

Chủ đề (2)

Với giải sách bài tập Toán 7 Bài 1: Tổng các góc của một tam giác sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 7 Bài 1. Mời các bạn đón xem:

Giải Sách bài tập Toán lớp 7 Bài 1: Tổng các góc của tam giác

Bài 1 trang 68 SBT Toán 7 Tập 2: Cho tam giác MHK vuông tại H. Ta có:

A. $\hat{M} + \hat{K} > 90 °$ ;

B. $\hat{M} + \hat{K} = 90 °$ ;

C. $\hat{M} + \hat{K} < 90 °$ ;

D. $\hat{M} + \hat{K} = 180 °$ .

Lời giải

Đáp án đúng là: B

Xét tam giác MHK vuông tại H ta có:

$\hat{M} + \hat{K} = 90 °$ (trong tam giác vuông, tổng hai góc nhọn bằng 90°).

Vậy ta chọn đáp án B.

Bài 2 trang 68 SBT Toán 7 Tập 2: Quan sát Hình 3.

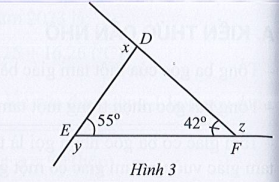
Sách bài tập Toán 7 Bài 1 (Cánh diều): Tổng các góc của một tam giác (ảnh 1)

a) Tính các số đo x, y, z.

b) Hãy nhận xét về tổng các số đo x + y + z.

Lời giải

a) • Tam giác DEF có x là số đo góc ngoài của tam giác tại đỉnh D.

Nên $x = \hat{DEF} + \hat{D F E}$ (tính chất góc ngoài của tam giác).

Do đó x = 55° + 42° = 97°.

• Ta có: $y + \hat{DEF} = 180 °$ (hai góc kề bù).

Suy ra $y = 180 ° - \hat{DEF} = 180 ° - 55 ° = 125 °$ .

• Ta có: $z + \hat{DFE} = 180 °$ (hai góc kề bù).

Suy ra $z = 180 ° - \hat{DFE} = 180 ° - 42 ° = 138 °$ .

Vậy x = 97°, y = 125° và z = 138°.

b) Ta có: x + y + z = 97° + 125° + 138° = 360°.

Vậy tổng số đo x + y + z của ba góc ngoài (kề bù với góc trong tam giác) luôn bằng 360°.

Bài 3 trang 68 SBT Toán 7 Tập 2:

a) Cho biết một góc nhọn của tam giác vuông bằng 40°. Tính số đo góc nhọn còn lại.

b) Cho một tam giác vuông có hai góc nhọn bằng nhau. Tính số đo mỗi góc nhọn đó.

Lời giải

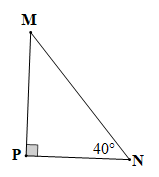
Sách bài tập Toán 7 Bài 1 (Cánh diều): Tổng các góc của một tam giác (ảnh 1)

Xét tam giác MNP vuông tại P ta có:

$\hat{M} + \hat{N} = 90 °$ (trong tam giác vuông, tổng hai góc nhọn bằng 90°)

Suy ra $\overset{︿}{M} = 90 ° - \overset{︿}{N} = 90 ° - 40 ° = 50 °$ .

Vậy số đo góc nhọn còn lại trong tam giác vuông đó là 50°.

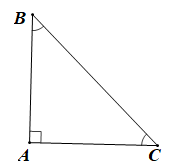
Sách bài tập Toán 7 Bài 1 (Cánh diều): Tổng các góc của một tam giác (ảnh 1)

Trong tam giác ABC vuông tại A ta có:

$\hat{B} + \hat{C} = 90 °$ (trong tam giác vuông, tổng hai góc nhọn bằng 90°).

Mà $\hat{B} = \hat{C}$ (giả thiết)

Suy ra $\hat{B} = \hat{C} = 90 ° : 2 = 45 °$ .

Vậy số đo mỗi góc nhọn của tam giác vuông đó là 45°.

Bài 4 trang 68 SBT Toán 7 Tập 2: Bạn Bình phát biểu: “Không có tam giác ABC nào mà $\hat{A} = 3 \hat{B}, \hat{B} = 3 \hat{C}$ và $\hat{C} = 14 °$ ”. Phát biểu của bạn Bình có đúng không? Vì sao?

Lời giải

Giả sử có tam giác ABC thỏa mãn $\hat{A} = 3 \hat{B}$ và $\hat{B} = 3 \hat{C}$

Khi đó $\hat{A} = 3 \hat{B} = 3.3 \hat{C} = 9 \hat{C}$ và $\hat{B} = 3 \hat{C}$ .

Suy ra $\hat{A} + \hat{B} + \hat{C} = 9 \hat{C} + \hat{3 C} + \hat{C} = 13 \hat{C}$

Mà $\hat{C} = 14 °$

Do đó $\hat{A} + \hat{B} + \hat{C} = 13.14 ° = 182 °$ . Điều này vô lí (vì tổng các góc của tam giác bằng 180°).

Do đó không có tam giác ABC nào thỏa mãn điều kiện $\hat{A} = 3 \hat{B}, \hat{B} = 3 \hat{C}$ và $\hat{C} = 14 °$ .

Vậy bạn Bình phát biểu đúng.

Bài 5 trang 68 SBT Toán 7 Tập 2: Cho tam giác ABC có $\hat{A} = 50 °, \hat{B} = 70 °$ . Tia phân giác của góc C cắt cạnh AB tại M. Tính số đo của $\hat{A M C}$ và $\hat{B M C}$ .

Lời giải

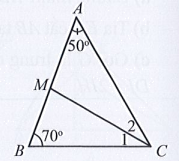
Sách bài tập Toán 7 Bài 1 (Cánh diều): Tổng các góc của một tam giác (ảnh 1)

Xét $∆$ ABC có: $\hat{A} + \hat{B} + \hat{C} = 180 °$ (định lí tổng ba góc của một tam giác).

Suy ra $\hat{A C B} = 180 ° - \hat{A} - \hat{B} = 180 ° - 50 ° - 70 ° = 60 °$ .

Vì tia CM là tia phân giác của $\hat{A C B}$ nên ta có:

$\hat{C_{1}} = \hat{C_{2}} = \frac{\hat{A C B}}{2} = \frac{60 °}{2} = 30 °$ .

Xét $∆$ AMC có: $\hat{A M C} + \hat{C_{2}} + \hat{A} = 180 °$ (tổng ba góc của một tam giác).

Suy ra $\hat{A M C} = 180 ° - \hat{C_{2}} - \hat{A} = 180 ° - 30 ° - 50 ° = 100 ° .$

Xét $∆$ BMC có: $\hat{B M C} + \hat{C_{1}} + \hat{B} = 180 °$ (tổng ba góc của một tam giác).

Suy ra $\hat{B M C} = 180 ° - \hat{C_{1}} - \hat{B} = 180 ° - 30 ° - 70 ° = 80 ° .$

Vậy $\hat{A M C} = 100 °, \hat{B M C} = 80 ° .$

Bài 6 trang 68 SBT Toán 7 Tập 2: Tính số đo các góc của tam giác ABC trong mỗi trường hợp sau:

a) $\hat{A} = \hat{B} = \hat{C}$ ;

b) $\hat{A} = 70 °$ và $\hat{C} - \hat{B} = 20 °$ ;

c) Số đo của $\hat{C} - \hat{B} = 20 °$ lần lượt tỉ lệ với 1; 2; 3.

Lời giải

a) Xét $∆$ ABC có: $\hat{A} + \hat{B} + \hat{C} = 180 °$ (tổng ba góc của một tam giác).

Mà $\hat{A} = \hat{B} = \hat{C}$

Do đó $\hat{A} = \hat{B} = \hat{C} = 180 ° : 3 = 60 °$ .

Vậy số đo mỗi góc A, B, C bằng 60°.

b) Xét $∆$ ABC có: $\hat{A} + \hat{B} + \hat{C} = 180 °$ (tổng ba góc của một tam giác).

Suy ra $\hat{B} + \hat{C} = 180 ° - \hat{A} = 180 ° - 70 ° = 110 °$ .

Lại có $\hat{C} - \hat{B} = 20 °$

Suy ra $\hat{B} = (110 ° - 20 °) : 2 = 45 °$

Khi đó $\hat{C} = 110 ° - 45 ° = 65 °$ .

Vậy số đo góc C là 65°, số đo góc B là 45°.

c) Số đo của $\hat{A}, \hat{B}, \hat{C}$ lần lượt tỉ lệ với 1; 2; 3 nên ta có $\frac{\hat{A}}{1} = \frac{\hat{B}}{2} = \frac{\hat{C}}{3}$ .

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

$\frac{\hat{A}}{1} = \frac{\hat{B}}{2} = \frac{\hat{C}}{3} = \frac{\hat{A} + \hat{B} + \hat{C}}{1 + 2 + 3} = \frac{180 °}{6} = 30 °$ .

Do đó

• $\hat{A} = 1.30 ° = 30 °;$

• $\hat{B} = 2.30 ° = 60 °;$

• $\hat{C} = 3.30 ° = 90 ° .$

Vậy số đo góc A, B, C lần lượt bằng 30°, 60° và 90°.

Bài 7 trang 68 SBT Toán 7 Tập 2: Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC tại H, AD là tia phân giác của $\hat{H A C}$ (Hình 4)

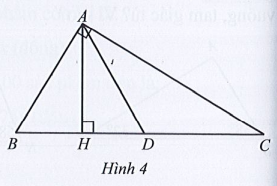
Sách bài tập Toán 7 Bài 1 (Cánh diều): Tổng các góc của một tam giác (ảnh 1)

a) Tìm các cặp góc có tổng số đo bằng 90°.

b) Cho $\hat{C} = 40 °$ . Tính số đo của $\hat{B}, \hat{B D A}, \hat{D A C} .$

c) Chứng minh: $\hat{B A H} = \hat{C}, \hat{C A H} = \hat{B}, \hat{B A D} = \hat{B D A} .$

Lời giải

a) Xét $∆$ ABC vuông tại A ta có:

$\hat{B} + \hat{C} = 90 °$ (trong tam giác vuông, tổng hai góc nhọn bằng 90°).

Xét $∆$ ABH vuông tại H ta có:

$\hat{B} + \hat{B A H} = 90 °$ (trong tam giác vuông, tổng hai góc nhọn bằng 90°).

Xét $∆$ ACH vuông tại H ta có:

$\hat{C} + \hat{C A H} = 90 °$ (trong tam giác vuông, tổng hai góc nhọn bằng 90°).

Xét $∆$ ADH vuông tại H ta có:

$\hat{A D H} + \hat{D A H} = 90 °$ (trong tam giác vuông, tổng hai góc nhọn bằng 90°).

Ta có: $\hat{B A C} = 90 ° = \hat{B A H} + \hat{H A C} = \hat{B A D} + \hat{D A C}$

Vậy các cặp góc có tổng số đo bằng 90° là:

$\hat{B A H}$ và $\hat{C A H}$ ; $\hat{B}$ và $\hat{C}$ ; $\hat{B}$ và $\hat{B A H}$ ; $\hat{C}$ và $\hat{C A H}$ ; $\hat{B A D}$ và $\hat{D A C}$ ; $\hat{H A D}$ và $\hat{A D H}$ .

b) • Do $\hat{B} + \hat{C} = 90 °$ (chứng minh câu a) nên $\hat{B} = 90 ° - \hat{C}$ .

Mà $\hat{C} = 40 °$ nên $\hat{B} = 90 ° - 40 ° = 50 °$ .

• Do $\hat{C} + \hat{C A H} = 90 °$ (chứng minh câu a)

Nên $\hat{C A H} = 90 ° - \hat{C} = 90 ° - 40 ° = 50 °$ .

Mà AD là tia phân giác của $\hat{C A H}$ (giả thiết)

Do đó $\hat{D A C} = \hat{D A H} = \frac{\hat{C A H}}{2} = \frac{50 °}{2} = 25 °$ .

• Do $\hat{A D H} + \hat{D A H} = 90 °$ (chứng minh câu a)

Nên $\hat{A D H} = 90 ° - \hat{D A H} = 90 ° - 25 ° = 65 °$ hay $\hat{B D A} = 65 ° .$

Vậy $\hat{B} = 50 °, \hat{B D A} = 65 °, \hat{D A C} = 25 ° .$

c) Vì $\hat{B} + \hat{B A H} = 90 °$ (chứng minh câu a)

Nên $\hat{B A H} = 90 ° - \hat{B} = 90 ° - 50 ° = 40 °$ .

Khi đó $\hat{B} = \hat{C A H} (= 50 °)$ , $\hat{C} = \hat{B A H} (= 40 °)$ .

Lại có $\hat{B A D} + \hat{D A C} = 90 °; \hat{A D H} + \hat{D A H} = 90 °$ (chứng minh câu a)

Mà $\hat{D A C} = \hat{D A H}$ suy ra $\hat{B A D} = \hat{A D H}$ hày $\hat{B A D} = \hat{B D A} .$

Vậy $\hat{B A H} = \hat{C}, \hat{C A H} = \hat{B}, \hat{B A D} = \hat{B D A} .$

Bài 8 trang 69 SBT Toán 7 Tập 2 : Cho tam giác ABC. Kẻ HB vuông góc với AC tại H. Kẻ CK vuông góc với AB tại K, BH cắt CK tại I (Hình 5).

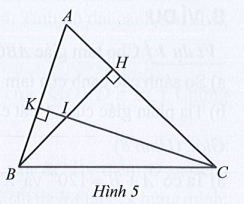
Sách bài tập Toán 7 Bài 1 (Cánh diều): Tổng các góc của một tam giác (ảnh 1)

Nếu $\hat{A} < 90 °$ thì khi đó ta có:

A. $\hat{A B H} < \hat{A C K}$ ;

B. $\hat{A B H} = \hat{A C K}$ ;

C. $\hat{A B H} > \hat{A C K}$ ;

D. $\hat{A B H} = 90 ° + \hat{A C K}$ .

Lời giải

Đáp án đúng là: B

• Xét $∆$ ABH vuông tại H ta có:

$\hat{A} + \hat{A B H} = 90 °$ (trong tam giác vuông, tổng hai góc nhọn bằng 90°).

Suy ra $\hat{A B H} = 90 ° - \hat{A}$ (1)

• Xét $∆$ ACK vuông tại K ta có:

$\hat{A} + \hat{A C K} = 90 °$ (trong tam giác vuông, tổng hai góc nhọn bằng 90°).

Suy ra $\hat{A C K} = 90 ° - \hat{A}$ (2)

Từ (1) và (2) ta có $\hat{A B H} = \hat{A C K} (= 90 ° - \hat{A})$ .

Vậy ta chọn đáp án B.

Bài 9 trang 69 SBT Toán 7 Tập 2: Cho tam giác ABC, tia phân giác của $\hat{B A C}$ cắt cạnh BC tại D. Tính số đo mỗi góc của tam giác ABC, biết $\hat{A D B} = 80 °$ và $\hat{B} = 1,5 \hat{C}$ .

Lời giải

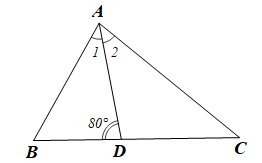
Sách bài tập Toán 7 Bài 1 (Cánh diều): Tổng các góc của một tam giác (ảnh 1)

• Xét $∆$ ABD có: ${\hat{A}}_{1} + \hat{B} + \hat{A D B} = 180 °$ (tổng ba góc của một tam giác)

Suy ra ${\hat{A}}_{1} + \hat{B} = 180 ° - \hat{A D B} = 180 ° - 80 ° = 100 °$

Khi đó ${\hat{A}}_{1} = 100 ° - \hat{B}$

Lại có $\hat{B} = 1,5 \hat{C}$

Suy ra ${\hat{A}}_{1} = 100 ° - 1,5 \hat{C}$ (1)

• Vì $\hat{A D B}$ là góc ngoài của tam giác ACD tại đỉnh D nên $\hat{A D B} = \hat{C} + {\hat{A}}_{2}$

Suy ra ${\hat{A}}_{2} = \hat{A D B} - \hat{C} = 80^{o} - \hat{C}$ (2)

• Ta có AD là tia phân giác của góc BAC nên ${\hat{A}}_{1} = {\hat{A}}_{2}$ (3)

Từ (1), (2), (3) ta có: $100 ° - 1,5 \hat{C} = 80 ° - \hat{C}$

Hay $1,5 \hat{C} - \hat{C} = 100 ° - 80 °$

Suy ra $\hat{C} = 40 °$ .

Do đó $\hat{B} = 1,5 \hat{C} = 1,5.40 ° = 60 °$ .

Xét $∆$ ABC có: $\hat{C} + \hat{B} + \hat{B A C} = 180 °$ (tổng ba góc của một tam giác).

Do đó $\hat{B A C} = 180 ° - \hat{C} - \hat{B} = 180 ° - 40 ° - 60 ° = 80 °$ .

Vậy $\hat{C} = 40 °, \hat{B} = 60 °, \hat{B A C} = 80 ° .$

Bài 10 trang 69 SBT Toán 7 Tập 2: Ở Hình 6 có $\hat{A} = \hat{B} = 60 °$ và Cx là tia phân giác của góc ACy. Chứng minh Cx song song với AB.

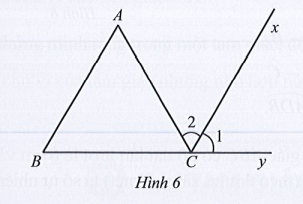
Sách bài tập Toán 7 Bài 1 (Cánh diều): Tổng các góc của một tam giác (ảnh 1)

Lời giải

Vì $\hat{A C y}$ là góc ngoài của $∆$ ABC tại đỉnh C nên $\hat{A C y} = \hat{A} + \hat{B}$ .

Do đó $\hat{A C y} = 60 ° + 60 ° = 120 °$ .

Vì Cx là tia phân giác của góc ACy nên ${\hat{C}}_{1} = {\hat{C}}_{2} = \frac{\hat{A C y}}{2} = \frac{120 °}{2} = 60 °$ .

Suy ra $\hat{B} = {\hat{C}}_{1}$ (cùng bằng 60°), mà chúng ở vị trí đồng vị nên Cx // AB.

Vậy Cx // AB.

Bài 11 trang 69 SBT Toán 7 Tập 2: Ở Hình 7 có $\hat{B A D} = \hat{B C D} = 90 °, \hat{A D B} = 15 °$ , AD song song với BC. Chứng minh AB song song với DC.

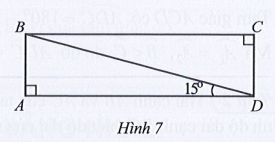
Sách bài tập Toán 7 Bài 1 (Cánh diều): Tổng các góc của một tam giác (ảnh 1)

Lời giải

Do AD // BC (giả thiết) nên $\hat{D B C} = \hat{A D B} = 15 °$ (hai góc so le trong).

Xét $∆$ BCD vuông tại C ta có:

$\hat{C B D} + \hat{C D B} = 90 °$ (trong tam giác vuông, tổng hai góc nhọn bằng 90°).

Suy ra $\hat{B D C} = 90 ° - \hat{D B C} = 90 ° - 15 ° = 75 °$ .

Xét $∆$ ABD vuông tại A ta có:

$\hat{A B D} + \hat{AD B} = 90 °$ (trong tam giác vuông, tổng hai góc nhọn bằng 90°).

Suy ra $\hat{A B D} = 90 ° - \hat{A D B} = 90 ° - 15 ° = 75 °$ .

Do đó $\hat{A B D} = \hat{B D C}$ (cùng bằng 75°)

Mà $\hat{A B D}$ và $\hat{B D C}$ ở vị trí so le trong nên AB // DC.

Vậy AB // DC.

Xem thêm lời giải sách bài tập Toán lớp 7 Cánh diều hay, chi tiết khác:

Bài 5. Phép chia đa thức một biến

Bài tập cuối chương 6

Bài 2. Quan hệ giữa góc và cạnh đối diện. Bất đẳng thức tam giác

Bài 3. Hai tam giác bằng nhau

Bài 4. Trường hợp bằng nhau thứ nhất của tam giác: cạnh – cạnh – cạnh

Câu hỏi liên quan

Cho tam giác ABC. Kẻ HB vuông góc với AC tại H. Kẻ CK vuông góc với AB tại K, BH cắt CK tại I (Hình 5)

Đáp án đúng là: B
Xem thêm

Cho tam giác MHK vuông tại H. Xét tam giác MHK vuông tại H

Đáp án đúng là: B
Xem thêm

Xem tất cả hỏi đáp với chuyên mục: Tổng các góc của một tam giác sbt

Được cập nhật 03/01/2024 182 lượt xem

Bởi Trang Quỳnh

Chủ đề: Giải sbt Toán 7 Tổng các góc của một tam giác

Bình luận (0)

Đăng nhập để có thể bình luận

Chưa có bình luận nào. Bạn hãy là người đầu tiên cho tôi biết ý kiến!

Bài viết cùng chủ đề

Giải sbt Toán 7 - CD

Giải SBT Toán 7 (Cánh diều) Bài tập cuối chương 7

Với giải sách bài tập Toán 7 Bài tập cuối chương 7 sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 7 chương 7. Mời các bạn đón xem:

163 9 tháng trước

Giải sbt Toán 7 - CD

Giải SBT Toán 7 (Cánh diều) Bài 13: Tính chất ba đường cao của tam giác

Với giải sách bài tập Toán 7 Bài 13: Tính chất ba đường cao của tam giác sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 7 Bài 13. Mời các bạn đón xem:

156 9 tháng trước

Giải sbt Toán 7 - CD

Giải SBT Toán 7 (Cánh diều) Bài 12: Tính chất ba đường trung trực của tam giác

Với giải sách bài tập Toán 7 Bài 12: Tính chất ba đường trung trực của tam giác sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 7 Bài 12. Mời các bạn đón xem:

160 9 tháng trước