Giải SBT Toán 7 (Cánh diều) Bài 2: Quan hệ giữa góc và cạnh đối diện. Bất đẳng thức tam giác

Giải Sách bài tập Toán lớp 7 Bài 2: Quan hệ giữa góc và cạnh dối diện. Bất đẳng thức tam giác

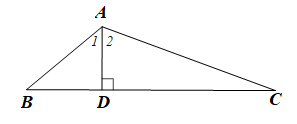
Bài 12 trang 70 SBT Toán 7 Tập 2: Cho tam giác ABC có $\widehat{A}=3\widehat{B}=6\widehat{C}$.

a) Tìm số đo góc lớn nhất, góc bé nhất của tam giác ABC.

b) Kẻ AD vuông góc với BC tại D. Chứng minh AD < BD.

Lời giải

a) Từ $\widehat{A}=3\widehat{B}=6\widehat{C}$ suy ra: $\frac{\widehat{A}}{6}=\frac{\widehat{B}}{2}=\frac{\widehat{C}}{1}$.

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

$\frac{\widehat{A}}{6}=\frac{\widehat{B}}{2}=\frac{\widehat{C}}{1}=\frac{\widehat{A}+\widehat{B}+\widehat{C}}{6+2+1}=\frac{180°}{9}=20°$.

Suy ra

• $\widehat{A}=20°.6=120°;$

• $\widehat{B}=20°.2=40°;$

• $\widehat{C}=20°.1=20°.$

Vậy trong tam giác ABC, số đo góc lớn nhất là $\widehat{A}=120°$, số đo góc bé nhất là $\widehat{C}=20°$.

b) Xét ∆ABD vuông tại D ta có:

${\widehat{A}}_1+\widehat{B}=90°$ (trong tam giác vuông, tổng hai góc nhọn bằng 90°).

Mà $\widehat{B}=40°$ (câu a)

Suy ra ${\widehat{A}}_1=90°-\widehat{B}=90°-40°=50°$.

Trong $∆$ADB có: ${\widehat{A}}_1>\widehat{B}$ (do 50° > 40°).

Suy ra BD > AD (trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn).

Vậy AD < BD.

Bài 13 trang 70 SBT Toán 7 Tập 2: Cho tam giác ABC có góc A tù. Trên cạnh AC lấy điểm D và E (D nằm giữa A và E). Chứng minh BA < BD < BE < BC.

Lời giải

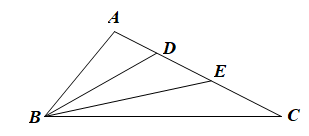
• Xét tam giác ABD có $\widehat{A}$là góc tù.

Nên BA < BD (trong tam giác tù, cạnh đối diện với góc tù là cạnh lớn nhất) (1)

• Vì $\widehat{BDE}$ là góc ngoài của tam giác ADB tại đỉnh D nên $\widehat{BDE}=\widehat{A}+\widehat{ABD}$.

Mà $\widehat{A}$là góc tù.

Do đó $\widehat{BDE}$ là góc tù.

Xét tam giác EBD có $\widehat{BDE}$là góc tù .

Nên BD < BE (trong tam giác tù, cạnh đối diện với góc tù là cạnh lớn nhất) (2)

• Vì $\widehat{BEC}$ là góc ngoài của tam giác AEB tại đỉnh E nên $\widehat{BEC}=\widehat{A}+\widehat{ABE}$

Mà $\widehat{A}$là góc tù.

Do đó $\widehat{BEC}$ là góc tù.

Xét tam giác EBC có $\widehat{BEC}$là góc tù.

Nên BE < BC (trong tam giác tù, cạnh đối diện với góc tù là cạnh lớn nhất) (3)

Từ (1), (2) và (3) suy ra BA < BD < BE < BC.

Vậy BA < BD < BE < BC.

Bài 14 trang 70, 71 SBT Toán 7 Tập 2: 

a) Cho tam giác ABC có AB = 15 cm, BC = 8 cm. Tính độ dài cạnh AC, biết độ dài của nó (theo đơn vị xăng-ti-mét) là một số nguyên tố lớn hơn bình phương của 4.

b) Độ dài ba cạnh của tam giác MNP tỉ lệ với 2; 3; 4. Tính độ dài cạnh lớn nhất, biết tổng độ dài hai cạnh là 20 cm.

Lời giải

a) Áp dụng bất đẳng thức tam giác cho tam giác ABC ta có:

AB – BC < AC < AB + BC

Hay 15 – 8 < AC < 15 + 8

Suy ra 7 < AC < 23.

Độ dài cạnh AC là một số nguyên tố lớn hơn bình phương của 4 tức là AC > 4² = 16 và AC là số nguyên tố.

Do đó AC = 17 cm hoặc AC = 19 cm.

Vậy AC = 17 cm hoặc AC = 19 cm.

b) Gọi độ dài ba cạnh của tam giác MNP là m, n, p với 0 < m ≤ n ≤ p.

Độ dài ba cạnh của tam giác MNP tỉ lệ với 2; 3; 4 nên ta có:

$\frac{m}{2}=\frac{n}{3}=\frac{p}{4}$.

Mặt khác tổng độ dài hai cạnh là 20 cm nên m + n = 20 (cm).

Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

$\frac{m}{2}=\frac{n}{3}=\frac{p}{4}=\frac{m+n}{2+3}=\frac{20}{5}=4$.

Suy ra p = 4 . 4 = 16 (cm).

Vậy độ dài cạnh lớn nhất của tam giác MNP là 16 cm.

Bài 15 trang 71 SBT Toán 7 Tập 2: Cho tam giác ABC có AB < AC, AD là tia phân giác của $\widehat{BAD}$ (D ∈ BC). Chứng minh $\widehat{ADB}<\widehat{ADC}$.

Lời giải

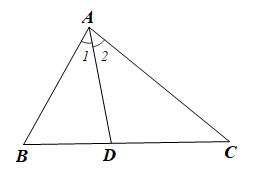
Xét tam giác ABC có AB < AC (giả thiết)

Suy ra $\widehat{C}<\widehat{B}$ (trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn).

Vì AD là tia phân giác của góc BAC nên ${\widehat{A}}_1={\widehat{A}}_2$.

Xét $∆$ABD có: ${\widehat{A}}_1+\widehat{B}+\widehat{ADB}=180°$ (tổng ba góc của một tam giác).

Suy ra $\widehat{ADB}=180°-{\widehat{A}}_1-\widehat{B}$ (1)

Xét $∆$ACD có: ${\widehat{A}}_2+\widehat{C}+\widehat{ADC}=180°$ (tổng ba góc của một tam giác).

Suy ra $\widehat{ADC}=180°-{\widehat{A}}_2-\widehat{C}$ (2)

Mà ${\widehat{A}}_1={\widehat{A}}_2$ (chứng minh trên) và $\widehat{B}>\widehat{C}$ (chứng minh trên) (3)

Từ (1), (2) và (3) ta có $\widehat{ADB}<\widehat{ADC}$

Vậy $\widehat{ADB}<\widehat{ADC}$.

Bài 16 trang 71 SBT Toán 7 Tập 2: Cho tam giác ABC có $\widehat{A}=110°$ và $\widehat{B}=\widehat{C}$. Trên cạnh BC lấy điểm D sao cho $\widehat{ADC}=105°$. Từ C kẻ đường thẳng song song với AD cắt tia BA tại E. Chứng minh:

a) AE < CE;

b) EC < BC < BE.

Lời giải

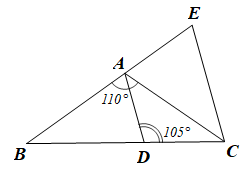
• Xét $∆$ACB có: $\widehat{BAC}+\widehat{BCA}+\widehat{B}=180°$ (tổng ba góc của một tam giác)

Mà $\widehat{BAC}=110°,$ $\widehat{B}=\widehat{ACB}$ (giả thiết)

Suy ra $\widehat{B}=\widehat{ACB}=\frac{180°-\widehat{BAC}}{2}=\frac{180°-110°}{2}=35°$.

• Ta có $\widehat{BAC}+\widehat{CAE}=180°$ (hai góc kề bù)

Suy ra $\widehat{CAE}=180°-\widehat{BAC}=180°-110°=70°$.

• Do AD // EC (giả thiết) nên $\widehat{ADC}+\widehat{ECD}={180}^o$ (hai góc trong cùng phía).

Suy ra $\widehat{ECD}={180}^o-\widehat{ADC}={180}^o-{105}^o={75}^o.$

Lại có $\widehat{ACB}+\widehat{ACE}=\widehat{ECD}$ (hai góc kề nhau)

Do đó $\widehat{ACE}=\widehat{ECD}-\widehat{ACB}=75°-{35}^o=40°.$

• Trong $∆$ACE có: $\widehat{ACE}<\widehat{CAE}$ (do 40° < 70°) 

Do đó AE < CE (trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn).

Vậy AE < CE.

b) Xét $∆$EBC có: $\widehat{E}+\widehat{BCE}+\widehat{B}=180°$ (tổng ba góc của một tam giác)

Mà $\widehat{BCE}=75°,\widehat{B}=35°$

Suy ra $\widehat{E}=180°-\widehat{B}-\widehat{BCE}=180°-35°-75°=70°$

Trong tam giác BCE có: $\widehat{B}<\widehat{E}<\widehat{BCE}$ (do 35° < 70° < 75°).

Nên EC < BC < BE (trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn).

Vậy EC < BC < BE.

Bài 17 trang 71 SBT Toán 7 Tập 2: Cho tam giác ABC, điểm D nằm giữa hai điểm B và C. Chứng minh AD nhỏ hơn nửa chu vi của tam giác ABC.

Lời giải

Xét $∆$ABD có: AD < AB + BD (bất đẳng thức tam giác) (1)

Xét $∆$ACD có AD < AC + DC (bất đẳng thức tam giác) (2)

Cộng theo vế của (1) và (2) ta có:

AD + AD < AB + BD + AC + DC

2AD < AB + AC + (BD + DC)

2AD < AB + AC + BC

Suy ra: $AD<\frac{AB+AC+BC}{2}$ 

Mà $\frac{AB+AC+BC}{2}$ là chu vi của tam giác ABC.

Vậy AD luôn nhỏ hơn nửa chu vi của tam giác ABC.

Bài 18* trang 71 SBT Toán 7 Tập 2: Chứng minh rằng trong một tam giác, độ dài cạnh lớn nhất sẽ lớn hơn hoặc bằng $\frac{1}{3}$ chu vi của tam giác nhưng nhỏ hơn nửa chu vi của tam giác đó.

Lời giải

Giả sử độ dài ba cạnh của tam giác là a, b, c với a ≥ b ≥ c > 0.

Theo bất đẳng thức tam giác ta có a < b + c.

Suy ra a + a < a + b + c.

Hay $a<\frac{a+b+c}{2}$   (1)

Vì a ≥ b, a ≥ c nên a + a + a ≥ a + b + c.

Hay 3a ≥ a + b + c.

Do đó $a\ge \frac{a+b+c}{3}$  (2)

Từ (1) và (2) suy ra: $\frac{a+b+c}{3}\le a<\frac{a+b+c}{2}$.

Mà chu vi của tam giác này là a + b + c.

Vậy trong một tam giác, độ dài cạnh lớn nhất sẽ lớn hơn hoặc bằng $\frac{1}{3}$ chi vi của tam giác nhưng nhỏ hơn nửa chu vi của tam giác đó.

Xem thêm lời giải sách bài tập Toán lớp 7 Cánh diều hay, chi tiết khác: 

Bài tập cuối chương 6

Bài 1. Tổng các góc của một tam giác

Bài 3. Hai tam giác bằng nhau

Bài 4. Trường hợp bằng nhau thứ nhất của tam giác: cạnh – cạnh – cạnh

Bài 5. Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh