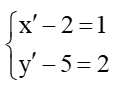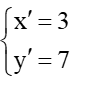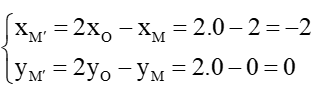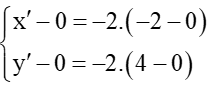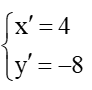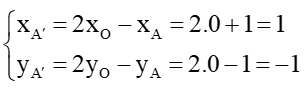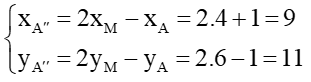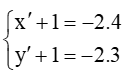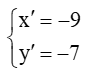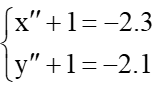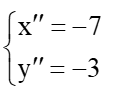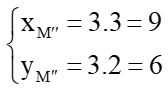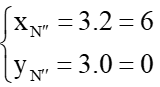Giải Chuyên đề Toán 11 Bài tập cuối chuyên đề 1 (Chân trời sáng tạo)

Giải Chuyên đề Toán 11 Bài tập cuối chuyên đề 1

Bài 1 trang 41 Chuyên đề Toán 11: Trong mặt phẳng tọa độ Oxy, cho điểm M(2; 5). Phép tịnh tiến theo vectơ $\overrightarrow{v}=\left(1;2\right)$ biến điểm M thành điểm có tọa độ là

A. (3; 1).

B. (1; 6).

C. (3; 7).

D. (4; 7).

Lời giải:

Đáp án đúng là: C

Ta đặt M’(x’; y’) là ảnh của điểm M qua $T_{\overrightarrow{v}}$.

Suy ra $\overrightarrow{{\mathrm{MM}}^{\text{'}}}=\overrightarrow{v}$ và $\overrightarrow{{\mathrm{MM}}^{\text{'}}}=\left(x^{\text{'}}-2;y^{\text{'}}-5\right)$

Do đó 

Vì vậy 

Vậy phép tịnh tiến theo vectơ biến điểm M thành điểm có tọa độ là (3; 7).

Do đó ta chọn phương án C.

Bài 2 trang 41 Chuyên đề Toán 11: Trong mặt phẳng tọa độ Oxy, qua phép đối xứng trục Oy, điểm A(3; 5) biến thành điểm nào trong các điểm sau?

A. (3; 5).

B. (–3; 5).

C. (3; –5).

D. (–3; –5).

Lời giải:

Đáp án đúng là: B

Ta đặt A’(x’; y’) là ảnh của điểm A qua phép đối xứng trục Oy.

Suy ra Oy là đường trung trực của đoạn AA’.

Do đó hai điểm A(3; 5) và A’ có cùng tung độ và có hoành độ đối nhau.

Vì vậy tọa độ điểm A’(–3; 5).

Vậy ta chọn phương án B.

Bài 3 trang 41 Chuyên đề Toán 11: Cho ba đường tròn có bán kính bằng nhau và đôi một tiếp xúc ngoài với nhau tạo thành hình ℋ. Hỏi ℋ có mấy trục đối xứng?

A. 0.

B. 1.

C. 2.

D. 3.

Lời giải:

Đáp án đúng là: D

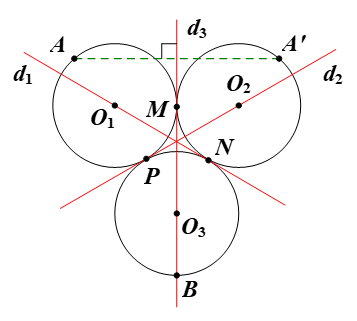
Gọi (O₁), (O₂), (O₃) là ba đường tròn thỏa mãn yêu cầu bài toán.

Gọi M, N, P lần lượt là tiếp điểm của các cặp đường tròn (O₁) và (O₂); (O₂) và (O₃); (O₁) và (O₃) (hình vẽ).

Chọn các đường thẳng d₁, d₂, d₃ lần lượt là các đường thẳng đi qua các cặp điểm O₁ và N; O₂ và P; O₃ và M.

Lấy điểm A nằm trên hình ℋ nhưng không nằm trên đường thẳng d₃.

Ta đặt A’ là ảnh của A qua phép đối xứng trục d₃.

Khi đó A’ nằm trên hình ℋ ban đầu.

Lấy điểm B nằm trên hình ℋ và nằm trên đường thẳng d₃.

Ta thấy B là ảnh của chính nó qua phép đối xứng trục d₃.

Tương tự như vậy, ta chọn các điểm khác bất kì nằm trên hình ℋ, ta cũng xác định được ảnh của điểm đó qua phép đối xứng trục d₃ trên hình ℋ.

Do đó phép đối xứng trục d₃ biến hình ℋ thành chính nó.

Vì vậy d₃ là trục đối xứng của hình ℋ.

Chứng minh tương tự với hai đường thẳng d₁, d₂, ta được d₁, d₂ cũng là trục đối xứng của hình ℋ.

Vậy hình ℋ có 3 trục đối xứng là các đường thẳng d₁, d₂, d₃.

Do đó ta chọn phương án D.

Bài 4 trang 41 Chuyên đề Toán 11: Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: x = 2. Trong các đường thẳng sau đường thẳng nào là ảnh của d qua phép đối xứng tâm O?

A. x = 2.

B. y = 2.

C. x = –2.

D. y = –2.

Lời giải:

Đáp án đúng là: C

Chọn điểm M(2; 0) ∈ d.

Ta đặt M’ = Đ_O(M).

Suy ra O là trung điểm MM’.

Do đó 

Vì vậy M’(–2; 0).

Đường thẳng d: x = 2 có vectơ pháp tuyến $\overrightarrow{n}=\left(1;0\right)$.

Gọi đường thẳng d’ là ảnh của đường thẳng d qua Đ_O.

Suy ra đường thẳng d’ song song hoặc trùng với d nên d’ có vectơ pháp tuyến $\overrightarrow{n}=\left(1;0\right)$.

Vậy đường thẳng d’ đi qua M’(–2; 0) và nhận $\overrightarrow{n}=\left(1;0\right)$ làm vectơ pháp tuyến nên có phương trình là:

1.(x + 2) + 0.(y – 0) = 0 ⇔ x + 2 = 0 ⇔ x = –2.

Do đó ta chọn phương án C.

Bài 5 trang 41 Chuyên đề Toán 11: Hình gồm hai đường tròn phân biệt có cùng bán kính có bao nhiêu tâm đối xứng?

A. Không có.

B. Một.

C. Hai.

D. Vô số.

Lời giải:

Đáp án đúng là: B

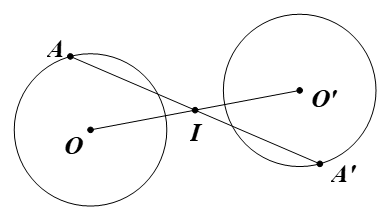
Giả sử (H) là hình gồm hai đường tròn phân biệt có cùng bán kính (O; R) và (O’; R).

Gọi I là trung điểm của đoạn OO’.

Suy ra O’ = Đ_I(O).

Gọi A là điểm bất kì trên (O; R).

Lấy điểm A’ sao cho I là trung điểm của AA’. Khi đó A’ = Đ_I(A).

Dễ dàng chứng minh được DOAI = DO’A’I (c.g.c)

Suy ra OA = O’A’ (hai cạnh tương ứng)

Mà OA = R nên O’A’ = R hay A’ nằm trên (O’; R).

Khi đó ta luôn xác định được một điểm A’ trên hình (H) sao cho A’ = Đ_I(A).

Tương tự như vậy, ta chọn các điểm khác bất kì trên hình (H), ta đều xác định được ảnh của các điểm đó qua Đ_I trên hình (H).

Vì vậy I là tâm đối xứng của hình (H).

Với mỗi điểm M bất kì sao cho M ≠ I, ta luôn có MO ≠ MO’.

Do đó O’ không phải là ảnh của O qua Đ_M.

Vậy hình gồm hai đường tròn phân biệt có cùng bán kính có 1 tâm đối xứng duy nhất là trung điểm của đoạn nối tâm.

Do đó ta chọn phương án B.

Bài 6 trang 41 Chuyên đề Toán 11: Trong mặt phẳng tọa độ Oxy, cho điểm M(1; 1). Hỏi các điểm sau điểm nào là ảnh của M qua phép quay tâm O với góc quay 45°?

A. M’(1; 1).

B. M’(1; 0).

C. $M^{\text{'}}\left(\sqrt{2};0\right)$.

D. $M^{\text{'}}\left(0;\sqrt{2}\right)$.

Lời giải:

Đáp án đúng là: D

Ta có $\overrightarrow{\mathrm{OM}}=\left(1;1\right)$. Suy ra $\mathrm{OM}=\sqrt{2}$.

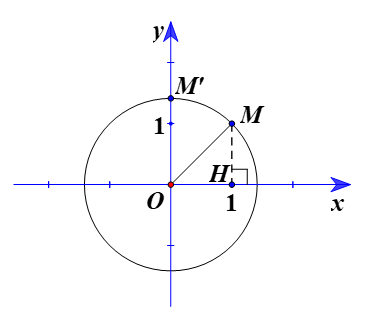
Vẽ đường tròn (C) tâm O, bán kính OM.

Ta có Q_{(O, 45°)} biến điểm M khác O thành điểm M’ sao cho ${\mathrm{OM}}^{\text{'}}=\mathrm{OM}=\sqrt{2}$ và (OM’, OM) = 45° hay $\widehat{{\mathrm{MOM}}^{\text{'}}}=45°$.

Kẻ MH ⊥ Ox tại H.

∆OMH vuông tại H: $\cos \widehat{\mathrm{MOH}}=\frac{\mathrm{OH}}{\mathrm{OM}}=\frac{1}{\sqrt{2}}$.

Suy ra $\widehat{\mathrm{MOH}}=45°$.

Ta có $\widehat{{\mathrm{HOM}}^{\text{'}}}=\widehat{\mathrm{HOM}}+\widehat{{\mathrm{MOM}}^{\text{'}}}=45°+45°=90°$.

Suy ra M’ ∈ Oy nên x_M’ = 0.

Mà ${\mathrm{OM}}^{\text{'}}=\sqrt{2}$ (chứng minh trên) nên $y_{M^{\text{'}}}=\sqrt{2}$.

Vậy tọa độ $M^{\text{'}}\left(0;\sqrt{2}\right)$.

Do đó ta chọn phương án D.

Bài 7 trang 41 Chuyên đề Toán 11: Cho tam giác đều tâm O. Hỏi có bao nhiêu phép quay tâm O với góc quay α, 0 < α ≤ 2π, biến tam giác trên thành chính nó?

A. Một.

B. Hai.

C. Ba.

D. Bốn.

Lời giải:

Đáp án đúng là: C

Gọi tam giác đã cho là ∆ABC.

⦁ ∆ABC đều có tâm O. Suy ra OA = OB = OC và $\widehat{\mathrm{ACB}}=\frac{\pi }{3}$.

Khi đó $\widehat{\mathrm{AOB}}=2\widehat{\mathrm{ACB}}=2.\frac{\pi }{3}=\frac{2\pi }{3}$.

Chứng minh tương tự, ta được $\widehat{\mathrm{BOC}}=\widehat{\mathrm{COA}}=\frac{2\pi }{3}$.

Vì vậy phép quay tâm O, góc quay $\alpha =\frac{2\pi }{3}$ biến các điểm A, B, C theo thứ tự thành các điểm B, C, A.

Do đó phép quay tâm O, góc quay $\alpha =\frac{2\pi }{3}$ biến ∆ABC thành chính nó.

⦁ Tương tự ta có phép quay tâm O, góc quay $\alpha =\frac{4\pi }{3}$ biến các điểm A, B, C theo thứ tự thành các điểm C, A, B.

Do đó phép quay tâm O, góc quay $\alpha =\frac{4\pi }{3}$ biến ∆ABC thành chính nó.

⦁ Phép quay tâm O, góc quay α = 2π biến các điểm A, B, C theo thứ tự thành các điểm A, B, C.

Do đó phép quay tâm O, góc quay α = 2π biến ∆ABC thành chính nó.

Vậy có 3 phép quay tâm O với các góc quay lần lượt là $\alpha =\frac{2\pi }{3}$; $\alpha =\frac{4\pi }{3}$; α = 2π thỏa mãn yêu cầu bài toán.

Do đó ta chọn phương án C.

Bài 8 trang 41 Chuyên đề Toán 11: Trong mặt phẳng tọa độ Oxy, cho điểm M(–2; 4). Phép vị tự tâm O tỉ số k = –2 biến điểm M thành điểm nào trong các điểm sau?

A. (–3; 4).

B. (–4; –8).

C. (4; –8).

D. (4; 8).

Lời giải:

Đáp án đúng là: C

Ta đặt M’(x’; y’) là ảnh của điểm M qua phép vị tự tâm O tỉ số k = –2.

Suy ra $\overrightarrow{{\mathrm{OM}}^{\text{'}}}=-2\overrightarrow{\mathrm{OM}}$

Do đó 

Vì vậy 

Vậy tọa độ M’(4; –8) thỏa mãn yêu cầu bài toán.

Do đó ta chọn phương án C.

Bài 9 trang 41 Chuyên đề Toán 11: Cho tam giác ABC. Vẽ về phía ngoài của tam giác các hình vuông ABEF, ACMN. Chứng minh BN bằng và vuông góc với FC.

Lời giải:

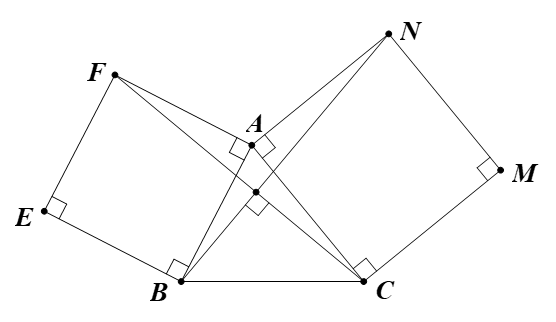
Vì ABEF là hình vuông nên AF = AB và $\left(\mathrm{AF},\mathrm{AB}\right)=\widehat{\mathrm{FAB}}=90°$.

Suy ra phép quay tâm A, góc quay 90° biến điểm F thành điểm B (1)

Vì ACMN là hình vuông nên AC = AN và $\left(\mathrm{AC},\mathrm{AN}\right)=\widehat{\mathrm{CAN}}=90°$.

Suy ra phép quay tâm A, góc quay 90° biến điểm C thành điểm N (2)

Từ (1), (2), ta thu được phép quay tâm A, góc quay 90° biến đoạn thẳng FC thành đoạn thẳng BN.

Do đó FC = BN và (FC, BN) = 90°.

Vậy FC = BN và FC ⊥ BN.

Bài 10 trang 41 Chuyên đề Toán 11: Cho đường tròn (O; R) và điểm I cố định khác O. Vẽ điểm M tùy ý trên (O). Tia phân giác của góc MOI cắt IM tại N. Điểm N di động trên đường nào khi M di động trên (O)?

Lời giải:

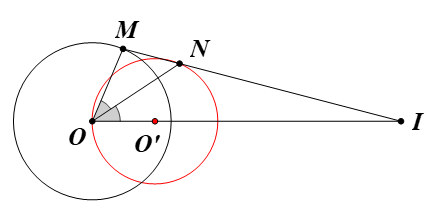
Đặt IO = d (d ≠ 0).

∆MOI có ON là đường phân giác, áp dụng tính chất đường phân giác, ta được: $\frac{\mathrm{NM}}{\mathrm{NI}}=\frac{\mathrm{OM}}{\mathrm{OI}}=\frac{R}{d}$.

Suy ra $\frac{\mathrm{NM}}{\mathrm{NI}}+1=\frac{R}{d}+1$

Khi đó $\frac{\mathrm{NM}+\mathrm{NI}}{\mathrm{NI}}=\frac{R+d}{d}$

Vì vậy $\frac{\mathrm{IM}}{\mathrm{NI}}=\frac{R+d}{d}$

Suy ra $\frac{\mathrm{IN}}{\mathrm{IM}}=\frac{d}{R+d}$.

Do đó $\mathrm{IN}=\frac{d}{R+d}.\mathrm{IM}$.

Vì vậy $\overrightarrow{\mathrm{IN}}=\frac{d}{R+d}.\overrightarrow{\mathrm{IM}}$ (do $\overrightarrow{\mathrm{IN}},\overrightarrow{\mathrm{IM}}$ cùng hướng).

Khi đó phép vị tự tâm I, tỉ số $k=\frac{d}{R+d}$ biến điểm M thành điểm N.

Giả sử khi M ở vị trí sao cho ba điểm O, M, I thẳng hàng (tức là, $\widehat{\mathrm{IOM}}=0°$) thì tia phân giác của góc MOI không thể cắt IM tại N.

Tức là, điểm N không tồn tại.

Ta đặt ${M^{\text{'}}}_0=V_{\left(I,\frac{d}{R+d}\right)}\left(M_0\right)$, với M₀ là điểm nằm trên đường tròn (O; R) sao cho ba điểm O, M₀, I thẳng hàng.

Vậy khi M chạy trên đường tròn (O; R) sao cho ba điểm O, M, I không thẳng hàng thì N chạy trên một đường tròn (O’; R’) cố định là ảnh của đường tròn (O; R) qua phép vị tự tâm I, tỉ số $k=\frac{d}{R+d}$ sao cho N ≠ M₀, với M₀ là điểm nằm trên đường tròn (O; R) sao cho ba điểm O, M₀, I thẳng hàng.

Bài 11 trang 41 Chuyên đề Toán 11: Cho điểm A chạy trên nửa đường tròn đường kính BC cố định. Vẽ về phía ngoài tam giác ABC hình vuông ABEF. Chứng minh rằng điểm E chạy trên một nửa đường tròn cố định.

Lời giải:

Gọi O là tâm của đường tròn đường kính BC.

Vì ABEF là hình vuông nên BA = BE và $\left(\mathrm{BA},\mathrm{BE}\right)=\widehat{\mathrm{ABE}}=90°$.

Suy ra phép quay tâm B, góc quay 90° biến điểm A thành điểm E.

Đặt C’ = Q_{(B, 90°)}(C) và O’ = Q_{(B, 90°)}(O).

Ta có B = Q_{(B, 90°)}(B).

Vậy khi điểm A chạy trên nửa đường tròn tâm O, đường kính BC cố định thì điểm E chạy trên nửa đường tròn tâm O’, đường kính BC’ cố định là ảnh của nửa đường tròn tâm O, đường kính BC qua phép quay tâm B, góc quay 90°.

Bài 12 trang 41 Chuyên đề Toán 11: Cho đường thẳng d: x + y + 2 = 0, đường tròn (C): x² + y² – 4x + 8y – 5 = 0.

a) Tìm ảnh của d qua phép đối xứng trục Ox.

b) Tìm ảnh của (C) qua phép đối xứng trục Oy.

Lời giải:

a) Chọn điểm M(–1; –1) ∈ d: x + y + 2 = 0.

Ta đặt M’ = Đ_Ox(M).

Suy ra Ox là đường trung trực của đoạn MM’ hay M, M’ đối xứng nhau qua Ox.

Do đó hai điểm M và M’ có cùng hoành độ và có tung độ đối nhau.

Vì vậy tọa độ M’(–1; 1).

Gọi N là giao điểm của d và Ox, khi đó y_N = 0, suy ra x_N = –2. Do đó N(–2; 0).

Gọi d’ là ảnh của d qua phép đối xứng trục Ox, khi đó đường thẳng d’ đi qua hai điểm M’(–1; 1) và N(–2; 0).

Ta có: $\overrightarrow{M^{\text{'}}N}=\left(-1;-1\right)\Rightarrow {\overrightarrow{n}}_{d^{\text{'}}}=\left(1;-1\right)$.

Đường thẳng d’ đi qua điểm N(–2; 0) và có vectơ pháp tuyến ${\overrightarrow{n}}_{d^{\text{'}}}=\left(1;-1\right)$nên có phương trình là:

1.(x + 2) – 1.(y – 0) = 0 hay x – y + 2 = 0.

b) Đường tròn (C): x² + y² – 4x + 8y – 5 = 0 có tâm I(2; –4), bán kính $R=\sqrt{2^2+{\left(-4\right)}^2-\left(-5\right)}=5$.

Gọi đường tròn (C’) là ảnh của đường tròn (C) qua Đ_Oy.

Suy ra (C’) là đường tròn có tâm là ảnh của I qua Đ_Oy và có bán kính R’ = R = 5.

Ta đặt I’ = Đ_Oy(I).

Suy ra Oy là đường trung trực của đoạn II’ hay I và I’ đối xứng nhau qua Oy

Do đó hai điểm I và I’ có cùng tung độ và có hoành độ đối nhau.

Vì vậy tọa độ I’(–2; –4).

Vậy phương trình đường tròn (C’) là ảnh của (C) qua Đ_Oy là: (x + 2)² + (y + 4)² = 25.

Bài 13 trang 41 Chuyên đề Toán 11: Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: x + 6y – 5 = 0.

a) Tìm ảnh của đường thẳng d qua phép đối xứng tâm O.

b) Tìm ảnh của đường thẳng d qua phép đối xứng tâm M(4; 6).

Lời giải:

a) Chọn điểm A(–1; 1) ∈ d.

Ta đặt A’ = Đ_O(A).

Suy ra O là trung điểm của AA’.

Do đó 

Vì vậy A’(1; –1).

Đường thẳng d có vectơ pháp tuyến $\overrightarrow{n}=\left(1;6\right)$.

Gọi d’ là ảnh của d qua Đ_O, suy ra d’ là đường thẳng song song hoặc trùng với d nên d’ nhận $\overrightarrow{n}=\left(1;6\right)$ làm vectơ pháp tuyến.

Vậy đường thẳng d’ đi qua A’(1; –1) và nhận $\overrightarrow{n}=\left(1;6\right)$ làm vectơ pháp tuyến nên có phương trình là:

1.(x – 1) + 6.(y + 1) = 0 hay x + 6y + 5 = 0.

b) Ta đặt A” = Đ_M(A).

Suy ra M là trung điểm AA”.

Do đó 

Vì vậy A”(9; 11).

Gọi d” là ảnh của d qua Đ_M, suy ra d’’ là đường thẳng song song hoặc trùng với d nên d’’ nhận $\overrightarrow{n}=\left(1;6\right)$ làm vectơ pháp tuyến.

Vậy đường thẳng d’’ đi qua A”(9; 11) và nhận $\overrightarrow{n}=\left(1;6\right)$ làm vectơ pháp tuyến nên có phương trình là:

1.(x – 9) + 6.(y – 11) = 0 hay x + 6y – 75 = 0.

Bài 14 trang 42 Chuyên đề Toán 11: Trong mặt phẳng tọa độ Oxy, cho M(3; 2), N(2; 0).

a) Tìm ảnh của các điểm M, N qua phép vị tự tâm I(–1; –1) tỉ số k = –2.

b) Tìm ảnh của các điểm M, N qua phép vị tự tâm O tỉ số k = 3.

Lời giải:

a) ⦁ Ta đặt M’(x’; y’) là ảnh của điểm M qua phép vị tự tâm I(–1; –1) tỉ số k = –2.

Suy ra $\overrightarrow{{\mathrm{IM}}^{\text{'}}}=-2\overrightarrow{\mathrm{IM}}$ với $\overrightarrow{{\mathrm{IM}}^{\text{'}}}=\left(x^{\text{'}}+1;y^{\text{'}}+1\right);\overrightarrow{\mathrm{IM}}=\left(4;3\right)$

Do đó 

Vì vậy 

Suy ra tọa độ M’(–9; –7).

⦁ Ta đặt N’(x’’; y’’) là ảnh của điểm N qua phép vị tự tâm I(–1; –1) tỉ số k = –2.

Suy ra $\overrightarrow{{\mathrm{IN}}^{\text{'}}}=-2\overrightarrow{\mathrm{IN}}$ với $\overrightarrow{{\mathrm{IN}}^{\text{'}}}=\left({x^{\text{'}}}^{\text{'}}+1;{y^{\text{'}}}^{\text{'}}+1\right);\overrightarrow{\mathrm{IN}}=\left(3;1\right)$

Do đó 

Vì vậy 

Suy ra tọa độ N’(–7; –3).

Vậy ảnh của các điểm M, N qua phép vị tự tâm I(–1; –1) tỉ số k = –2 có tọa độ lần lượt là M’(–9; –7), N’(–7; –3).

b) ⦁ Ta đặt $M^{\text{'}\text{'}}\left(x_{M^{\text{'}\text{'}}};y_{M^{\text{'}\text{'}}}\right)$ là ảnh của điểm M qua phép vị tự tâm O tỉ số k = 3.

Suy ra $\overrightarrow{O{M^{\text{'}}}^{\text{'}}}=3\overrightarrow{\mathrm{OM}}$ với $\overrightarrow{O{M}^{\text{'}\text{'}}}=\left(x_{M^{\text{'}\text{'}}};y_{M^{\text{'}\text{'}}}\right);\overrightarrow{\mathrm{OM}}=\left(3;2\right)$

Do đó 

Suy ra tọa độ M”(9; 6).

⦁ Ta đặt $N^{\text{'}\text{'}}\left(x_{N^{\text{'}\text{'}}};y_{N^{\text{'}\text{'}}}\right)$ là ảnh của điểm N qua phép vị tự tâm O tỉ số k = 3.

Suy ra $\overrightarrow{O{N}^{\text{'}\text{'}}}=3\overrightarrow{\mathrm{ON}}$ với $\overrightarrow{O{N}^{\text{'}\text{'}}}=\left(x_{N^{\text{'}\text{'}}};y_{N^{\text{'}\text{'}}}\right);\overrightarrow{\mathrm{ON}}=\left(2;0\right)$

Do đó 

Suy ra tọa độ N”(6; 0).

Vậy ảnh của các điểm M, N qua phép vị tự tâm O tỉ số k = 3 có tọa độ lần lượt là M”(9; 6), N”(6; 0).

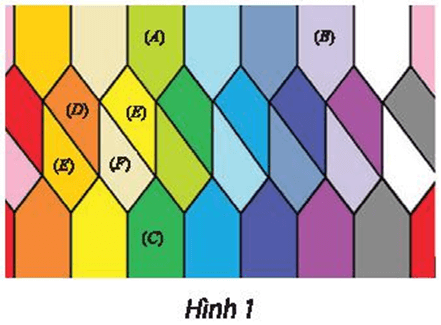
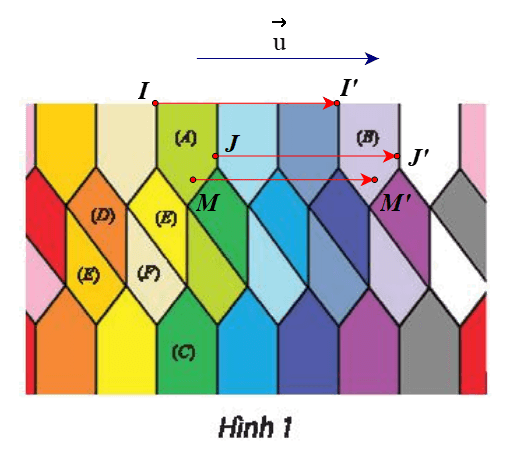
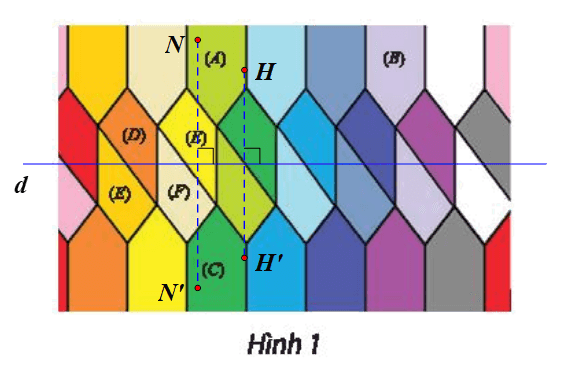
Bài 15 trang 42 Chuyên đề Toán 11: Cho Hình 1.

a) Tìm phép biến hình f biến hình (A) thành hình (B).

b) Tìm phép biến hình g biến hình (A) thành hình (C).

c) Tìm các phép biến hình biến hình (D) thành lần lượt các hình (E), (F), (G).

Lời giải:

a) Gọi I là một điểm trên hình (A) và I’ là một điểm trên hình (B) có vị trí tương ứng với điểm I trên hình (A) (hình vẽ).

Giả sử là vectơ có phương vuông góc với trục đối xứng của hình (A), độ dài bằng độ dài từ điểm I đến điểm I’ (hình vẽ).

Tức là, $\overrightarrow{u}=\overrightarrow{{\mathrm{II}}^{\text{'}}}$.

Gọi J là một điểm bất kì trên hình (A).

Lấy điểm J’ sao cho $\overrightarrow{{\mathrm{JJ}}^{\text{'}}}=\overrightarrow{u}$.

Khi đó J’ là một điểm trên hình (B) có vị trí tương ứng với điểm J trên hình (A).

Tương tự như vậy, với mỗi điểm M bất kì trên hình (A), ta lấy điểm M’ sao cho $\overrightarrow{{\mathrm{MM}}^{\text{'}}}=\overrightarrow{u}$ thì ta được tập hợp các điểm M’ tạo thành hình (B).

Vậy phép biến hình f cần tìm là phép tịnh tiến theo .

b) Chọn đường thẳng d như hình vẽ.

Lấy điểm H bất kì nằm trên hình (A).

Ta đặt H’ = Đ_d(H).

Khi đó H’ nằm trên hình (C) có vị trí tương ứng với điểm H trên hình (A).

Tương tự như vậy, với mỗi điểm N bất kì trên hình (A), ta lấy điểm N’ sao cho N’ = Đ_d(N) thì ta được tập hợp các điểm N’ tạo thành hình (C).

Vậy phép biến hình g cần tìm là phép đối xứng trục d, với d là đường thẳng trên Hình 1 (như hình vẽ).

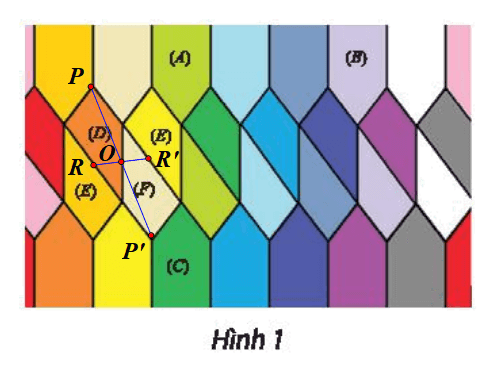
c) ⦁ Phép biến hình biến hình (D) thành hình (E):

Gọi R là một điểm bất kì trên hình (D).

Giả sử O là trung điểm của cạnh bên hình thang (D) (như hình vẽ).

Lấy điểm R’ sao cho R’ = Đ_O(R).

Khi đó R’ là một điểm trên hình (F) có vị trí tương ứng với điểm R trên hình (D).

Tương tự như vậy, với mỗi điểm P bất kì trên hình (D), ta lấy điểm P’ sao cho P’ = Đ_O(P) thì ta được tập hợp các điểm P’ tạo thành hình (F).

Vậy phép đối xứng tâm O biến hình (D) thành hình (F).

⦁ Phép biến hình biến hình (D) thành hình (G):

Bài 16 trang 42 Chuyên đề Toán 11: Gọi O được gọi là tâm đối xứng quay bậc n (n ∈ ℕ*) của hình ℋ nếu sau khi thực hiện phép quay $Q_{\left(O,\frac{360°}{n}\right)}$ ta lại được chính hình ℋ. Hình có tâm đối xứng quay bậc n gọi là hình đối xứng quay bậc n. Tìm các hình đối xứng quay trong Hình 2.

Lời giải:

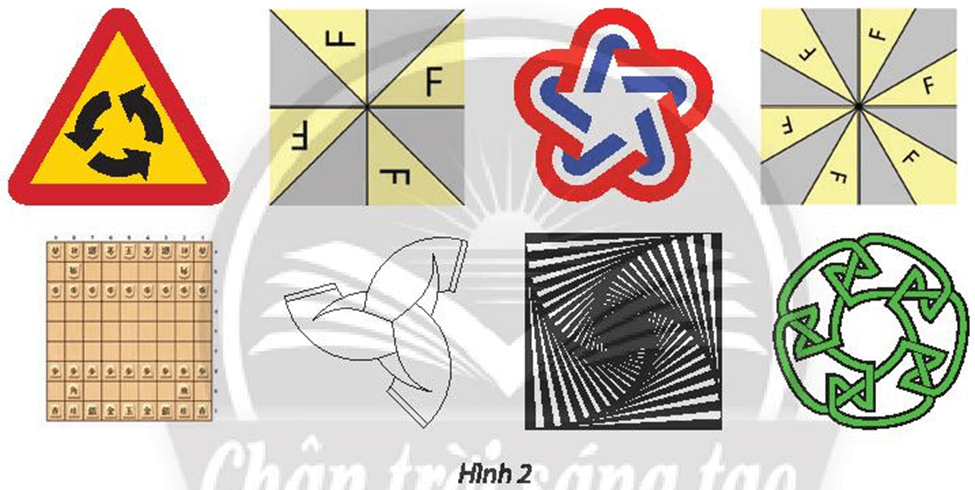
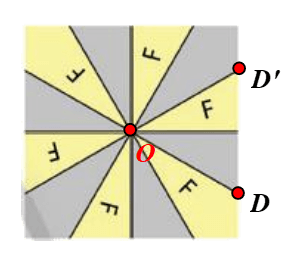
Ta đặt tên cho các hình vẽ trong Hình 2 theo thứ tự từ trái qua phải, từ trên xuống dưới là: a, b, c, d, e, f, g, h.

⦁ Xét Hình 2a: biển báo có dạng hình tam giác đều.

Gọi O là tâm đường tròn ngoại tiếp tam giác, điểm A là một đỉnh của tam giác.

Phép quay tâm O, góc quay 120° biến điểm A thành điểm A’.

Khi đó ta thấy điểm A’ nằm trên Hình 2a ban đầu.

Tương tự, ta chọn các điểm khác bất kì trên Hình 2a.

Khi đó qua phép quay tâm O, góc quay 120°, ta cũng xác định được ảnh của các điểm đó trên Hình 2a ban đầu.

Vì vậy phép quay biến Hình 2a thành chính nó là phép quay tâm O, góc quay 120°.

Ta có $\frac{360°}{n}=120°$. Suy ra n = 3 ∈ ℕ*.

Vì vậy Hình 2a có tâm đối xứng quay bậc 3.

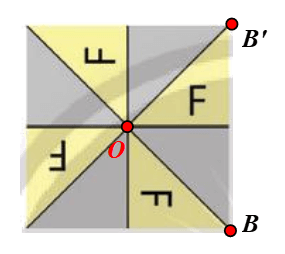
⦁ Xét Hình 2b: có dạng hình vuông.

Gọi O là tâm hình vuông và B là một đỉnh của hình vuông.

Phép quay tâm O, góc quay 90° biến điểm B thành điểm B’.

Khi đó ta thấy điểm B’ nằm trên Hình 2b ban đầu.

Tương tự, ta chọn các điểm khác bất kì trên Hình 2b.

Khi đó qua phép quay tâm O, góc quay 90°, ta cũng xác định được ảnh của các điểm đó trên Hình 2b ban đầu.

Vì vậy phép quay biến Hình 2b thành chính nó là phép quay tâm O, góc quay 90°.

Ta có $\frac{360°}{n}=90°$. Suy ra n = 4 ∈ ℕ*.

Vì vậy Hình 2b có tâm đối xứng quay bậc 4.

⦁ Xét Hình 2c:

Chọn hai điểm O, C như hình vẽ.

Phép quay tâm O, góc quay 72° biến điểm C thành điểm C’.

Khi đó ta thấy điểm C’ nằm trên Hình 2c ban đầu.

Tương tự, ta chọn các điểm khác bất kì trên Hình 2c.

Khi đó qua phép quay tâm O, góc quay 72°, ta cũng xác định được ảnh của các điểm đó trên Hình 2c ban đầu.

Vì vậy phép quay biến Hình 2c thành chính nó là phép quay tâm O, góc quay 72°.

Ta có $\frac{360°}{n}=72°$. Suy ra n = 5 ∈ ℕ*.

Vì vậy Hình 2c có tâm đối xứng quay bậc 5.

⦁ Xét Hình 2d: có dạng hình vuông

Gọi O là tâm hình vuông. Chọn điểm D như hình vẽ.

Phép quay tâm O, góc quay 60° biến điểm D thành điểm D’.

Khi đó ta thấy điểm D’ nằm trên Hình 2d ban đầu.

Tương tự, ta chọn các điểm khác bất kì trên Hình 2d.

Khi đó qua phép quay tâm O, góc quay 60°, ta cũng xác định được ảnh của các điểm đó trên Hình 2d ban đầu.

Vì vậy phép quay biến Hình 2d thành chính nó là phép quay tâm O, góc quay 60°.

Ta có $\frac{360°}{n}=60°$. Suy ra n = 6 ∈ ℕ*.

Vì vậy Hình 2d có tâm đối xứng quay bậc 6.

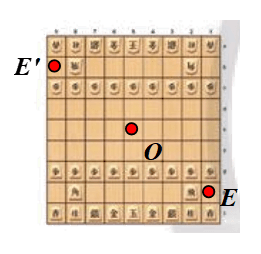
⦁ Xét Hình 2e: có dạng hình vuông.

Gọi O là tâm hình vuông. Chọn điểm E như hình vẽ.

Phép quay tâm O, góc quay 180° biến điểm E thành điểm E’.

Khi đó ta thấy điểm E’ nằm trên Hình 2e ban đầu.

Tương tự, ta chọn các điểm khác bất kì trên Hình 2e.

Khi đó qua phép quay tâm O, góc quay 180°, ta cũng xác định được ảnh của các điểm đó trên Hình 2e ban đầu.

Vì vậy phép quay biến Hình 2e thành chính nó là phép quay tâm O, góc quay 180°.

Ta có $\frac{360°}{n}=180°$. Suy ra n = 2 ∈ ℕ*.

Vì vậy Hình 2e có tâm đối xứng quay bậc 2.

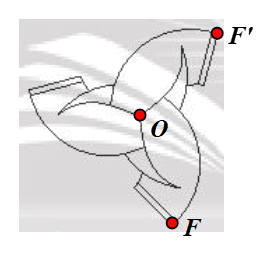
⦁ Xét Hình 2f:

Chọn hai điểm O, F như hình vẽ.

Phép quay tâm O, góc quay 120° biến điểm F thành điểm F’.

Khi đó ta thấy điểm F’ nằm trên Hình 2f ban đầu.

Tương tự, ta chọn các điểm khác bất kì trên Hình 2f.

Khi đó qua phép quay tâm O, góc quay 120°, ta cũng xác định được ảnh của các điểm đó trên Hình 2f ban đầu.

Vì vậy phép quay biến Hình 2f thành chính nó là phép quay tâm O, góc quay 120°.

Ta có $\frac{360°}{n}=120°$. Suy ra n = 3 ∈ ℕ*.

Vì vậy Hình 2f có tâm đối xứng quay bậc 3.

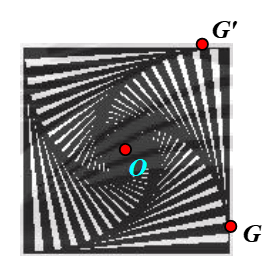
⦁ Xét Hình 2g: có dạng hình vuông.

Gọi O là tâm hình vuông. Chọn điểm G như hình vẽ.

Phép quay tâm O, góc quay 90° biến điểm G thành điểm G’.

Khi đó ta thấy điểm G’ nằm trên Hình 2g ban đầu.

Tương tự, ta chọn các điểm khác bất kì trên Hình 2g.

Khi đó qua phép quay tâm O, góc quay 90°, ta cũng xác định được ảnh của các điểm đó trên Hình 2g ban đầu.

Vì vậy phép quay biến Hình 2g thành chính nó là phép quay tâm O, góc quay 90°.

Ta có $\frac{360°}{n}=90°$. Suy ra n = 4 ∈ ℕ*.

Vì vậy Hình 2g có tâm đối xứng quay bậc 4.

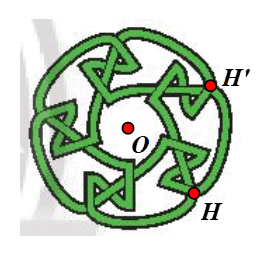
⦁ Xét Hình 2h: có dạng hình tròn

Gọi O là tâm hình tròn. Chọn điểm H như hình vẽ.

Phép quay tâm O, góc quay 72° biến điểm H thành điểm H’.

Khi đó ta thấy điểm H’ nằm trên Hình 2h ban đầu.

Tương tự, ta chọn các điểm khác bất kì trên Hình 2h.

Khi đó qua phép quay tâm O, góc quay 72°, ta cũng xác định được ảnh của các điểm đó trên Hình 2h ban đầu.

Vì vậy phép quay biến Hình 2h thành chính nó là phép quay tâm O, góc quay 72°.

Ta có $\frac{360°}{n}=72°$. Suy ra n = 5 ∈ ℕ*.

Vì vậy Hình 2h có tâm đối xứng quay bậc 5.

Vậy tất cả các hình trong Hình 2 đều là hình đối xứng quay có bậc lần lượt là 3; 4; 5; 6; 2; 3; 4; 5 (tính thứ tự các hình từ trái qua phải và từ trên xuống dưới).

Bài 17 trang 42 Chuyên đề Toán 11: Thấu kính hội tụ có thể cho ảnh thật hoặc ảnh ảo A’B’ của vật AB. Tìm phép vị tự biến AB thành A’B’ trong Hình 3 và Hình 4.

Lời giải:

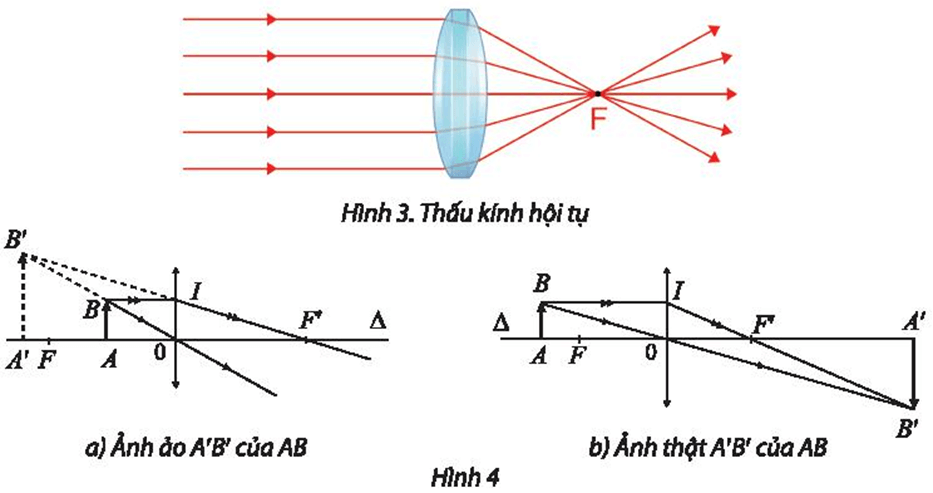
⦁ Ta xét Hình 4a:

Để tìm phép vị tự biến vật AB thành ảnh A’B’, ta tìm phép vị tự biến A, B lần lượt thành A’, B’.

Ta có AA’ cắt BB’ tại O.

Vì ba điểm O, A, A’ thẳng hàng và A, A’ nằm cùng phía đối với O.

Suy ra $\overrightarrow{{\mathrm{OA}}^{\text{'}}}=k\overrightarrow{\mathrm{OA}}$, với k > 0.

Do đó V_{(O, k)}(A) = A’ và OA’ = k.OA.

Vì vậy $k=\frac{{\mathrm{OA}}^{\text{'}}}{\mathrm{OA}}$.

Xét ∆OA’B’ và ∆OAB, có:

$\widehat{\mathrm{AOB}}$ chung;

$\widehat{{\mathrm{OA}}^{\text{'}}{B}^{\text{'}}}=\widehat{\mathrm{OAB}}=90°$.

Do đó ${\mathrm{\Delta OA}}^{\text{'}}{B}^{\text{'}}\backsim \mathrm{\Delta OAB}$ (g.g).

Suy ra $\frac{{\mathrm{OB}}^{\text{'}}}{\mathrm{OB}}=\frac{{\mathrm{OA}}^{\text{'}}}{\mathrm{OA}}=k$.

Vì vậy OB’ = k.OB.

Mà ba điểm O, B, B’ thẳng hàng và B, B’ nằm cùng phía đối với O.

Suy ra $\overrightarrow{{\mathrm{OB}}^{\text{'}}}=k\overrightarrow{\mathrm{OB}}$.

Do đó V_{(O, k)}(B) = B’.

Vậy phép vị tự tâm O, tỉ số $k=\frac{{\mathrm{OA}}^{\text{'}}}{\mathrm{OA}}$ biến vật AB thành ảnh A’B’.

⦁ Ta xét Hình 4b:

Để tìm phép vị tự biến vật AB thành ảnh A’B’, ta tìm phép vị tự biến A, B lần lượt thành A’, B’.

Ta có AA’ cắt BB’ tại O.

Vì ba điểm O, A, A’ thẳng hàng và A, A’ nằm khác phía đối với O.

Suy ra $\overrightarrow{{\mathrm{OA}}^{\text{'}}}=k\overrightarrow{\mathrm{OA}}$, với k < 0.

Do đó V_{(O, k)}(A) = A’ và OA’ = |k|.OA.

Vì vậy $k=-\frac{{\mathrm{OA}}^{\text{'}}}{\mathrm{OA}}$.

Xét ∆OA’B’ và ∆OAB, có:

$\widehat{A^{\text{'}}{\mathrm{OB}}^{\text{'}}}=\widehat{\mathrm{AOB}}$ (đối đỉnh);

$\widehat{{\mathrm{OA}}^{\text{'}}{B}^{\text{'}}}=\widehat{\mathrm{OAB}}=90°$.

Do đó ${\mathrm{\Delta OA}}^{\text{'}}{B}^{\text{'}}\backsim \mathrm{\Delta OAB}$ (g.g).

Suy ra $\frac{{\mathrm{OB}}^{\text{'}}}{\mathrm{OB}}=\frac{{\mathrm{OA}}^{\text{'}}}{\mathrm{OA}}=\mathrm{|k|}$.

Vì vậy OB’ = |k|.OB.

Mà ba điểm O, B, B’ thẳng hàng và B, B’ nằm khác phía đối với O.

Suy ra $\overrightarrow{{\mathrm{OB}}^{\text{'}}}=k\overrightarrow{\mathrm{OB}}$

Do đó V_{(O, k)}(B) = B’.

Vậy phép vị tự tâm O, tỉ số $k=-\frac{{\mathrm{OA}}^{\text{'}}}{\mathrm{OA}}$ biến vật AB thành ảnh A’B’.

Bài 18 trang 42 Chuyên đề Toán 11: Cho tam giác ABC có góc B, góc C đều là góc nhọn. Nêu cách vẽ hình chữ nhật DEFG có đỉnh D, đỉnh E thuộc cạnh BC, đỉnh F, đỉnh G thuộc cạnh AC, AB và có EF = 2DE.

Lời giải:

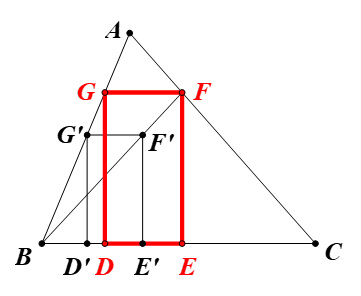
⦁ Phân tích:

Lấy điểm G’ bất kì trên AB.

Dựng hình chữ nhật D’E’F’G’ có E’F’ = 2D’E’ và hai đỉnh D’, E’ thuộc BC.

Đường thẳng BF’ cắt AC tại F.

Do D’E’F’G’ là hình chữ nhật nên G’D’ ⊥ D’E’ hay G’D’ ⊥ BC.

Mà GD ⊥ BC (do DEFG là hình chữ nhật).

Nên G’D’ // GD.

Chứng minh tương tự, ta được E’F’ // EF.

Vì D’E’F’G’ là hình chữ nhật nên G’F’ // D’E’ hay G’F’ // BC.

Mà GF // BC (do DEFG là hình chữ nhật).

Suy ra GF // G’F’.

Áp dụng định lí Thales, ta được $\frac{\mathrm{BG}}{{\mathrm{BG}}^{\text{'}}}=\frac{\mathrm{BF}}{{\mathrm{BF}}^{\text{'}}}$.

Suy ra ${\mathrm{BF}}^{\text{'}}=\frac{{\mathrm{BG}}^{\text{'}}}{\mathrm{BG}}.\mathrm{BF}$.

Mà $\overrightarrow{{\mathrm{BF}}^{\text{'}}},\overrightarrow{\mathrm{BF}}$ cùng hướng.

Do đó $\overrightarrow{{\mathrm{BF}}^{\text{'}}}=\frac{{\mathrm{BG}}^{\text{'}}}{\mathrm{BG}}.\overrightarrow{\mathrm{BF}}$.

Vì vậy ${\text{F}}^{\text{'}}=V_{\left(B,\frac{{\mathrm{BG}}^{\text{'}}}{\mathrm{BG}}\right)}\left(F\right)$ (1)

Chứng minh tương tự, ta được $D^{\text{'}}=V_{\left(B,\frac{{\mathrm{BG}}^{\text{'}}}{\mathrm{BG}}\right)}\left(D\right)$ và $E^{\text{'}}=V_{\left(B,\frac{{\mathrm{BG}}^{\text{'}}}{\mathrm{BG}}\right)}\left(E\right)$ (2)

Lại có $G^{\text{'}}=V_{\left(B,\frac{{\mathrm{BG}}^{\text{'}}}{\mathrm{BG}}\right)}\left(G\right)$ (3)

Từ (1), (2), (3), ta thu được $V_{\left(B,\frac{{\mathrm{BG}}^{\text{'}}}{\mathrm{BG}}\right)}$ biến hình chữ nhật D’E’F’G’ thành hình chữ nhật DEFG. Từ đó, ta suy ra cách dựng hình chữ nhật DEFG.

⦁ Cách dựng:

Lấy điểm G’ tùy ý trên AB.

Dựng hình chữ nhật D’E’F’G’ có E’F’ = 2D’E’, hai đỉnh D’, E’ nằm trên BC.

Đường thẳng BF’ cắt AC tại F.

Đường thẳng qua F song song với BC cắt AB tại G.

Gọi D, E lần lượt là hình chiếu của G, F lên BC.

Vậy ta đã dựng xong hình chữ nhật DEFG.

Xem thêm các bài giải Chuyên đề học tập Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác:

Bài 6: Phép vị tự

Bài 7: Phép đồng dạng

Bài 1: Đồ thị

Bài 2: Đường đi Euler và đường đi Hamilton

Bài 3: Bài toán tìm đường đi ngắn nhất