Cho đường tròn (O; R) và điểm I cố định khác O. Vẽ điểm M tùy ý trên (O). Tia phân giác của góc MOI

Bài 10 trang 41 Chuyên đề Toán 11: Cho đường tròn (O; R) và điểm I cố định khác O. Vẽ điểm M tùy ý trên (O). Tia phân giác của góc MOI cắt IM tại N. Điểm N di động trên đường nào khi M di động trên (O)?

Trả lời

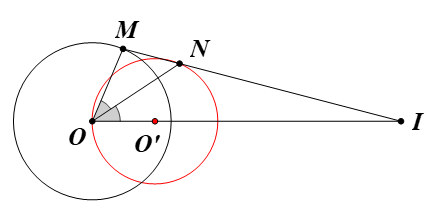
Đặt IO = d (d ≠ 0).

∆MOI có ON là đường phân giác, áp dụng tính chất đường phân giác, ta được: $\frac{\mathrm{NM}}{\mathrm{NI}}=\frac{\mathrm{OM}}{\mathrm{OI}}=\frac{R}{d}$.

Suy ra $\frac{\mathrm{NM}}{\mathrm{NI}}+1=\frac{R}{d}+1$

Khi đó $\frac{\mathrm{NM}+\mathrm{NI}}{\mathrm{NI}}=\frac{R+d}{d}$

Vì vậy $\frac{\mathrm{IM}}{\mathrm{NI}}=\frac{R+d}{d}$

Suy ra $\frac{\mathrm{IN}}{\mathrm{IM}}=\frac{d}{R+d}$.

Do đó $\mathrm{IN}=\frac{d}{R+d}.\mathrm{IM}$.

Vì vậy $\overrightarrow{\mathrm{IN}}=\frac{d}{R+d}.\overrightarrow{\mathrm{IM}}$ (do $\overrightarrow{\mathrm{IN}},\overrightarrow{\mathrm{IM}}$ cùng hướng).

Khi đó phép vị tự tâm I, tỉ số $k=\frac{d}{R+d}$ biến điểm M thành điểm N.

Giả sử khi M ở vị trí sao cho ba điểm O, M, I thẳng hàng (tức là, $\widehat{\mathrm{IOM}}=0°$) thì tia phân giác của góc MOI không thể cắt IM tại N.

Tức là, điểm N không tồn tại.

Ta đặt ${M^{\text{'}}}_0=V_{\left(I,\frac{d}{R+d}\right)}\left(M_0\right)$, với M₀ là điểm nằm trên đường tròn (O; R) sao cho ba điểm O, M₀, I thẳng hàng.

Vậy khi M chạy trên đường tròn (O; R) sao cho ba điểm O, M, I không thẳng hàng thì N chạy trên một đường tròn (O’; R’) cố định là ảnh của đường tròn (O; R) qua phép vị tự tâm I, tỉ số $k=\frac{d}{R+d}$ sao cho N ≠ M₀, với M₀ là điểm nằm trên đường tròn (O; R) sao cho ba điểm O, M₀, I thẳng hàng.

Xem thêm các bài giải Chuyên đề Toán 11 Chân trời sáng tạo hay, chi tiết khác:

Bài 6: Phép vị tự

Bài 7: Phép đồng dạng

Bài tập cuối chuyên đề 1

Bài 1: Đồ thị

Bài 2: Đường đi Euler và đường đi Hamilton

Bài 3: Bài toán tìm đường đi ngắn nhất