Cho tam giác ABC có góc B, góc C đều là góc nhọn. Nêu cách vẽ hình chữ nhật DEFG có đỉnh D, đỉnh E

Bài 18 trang 42 Chuyên đề Toán 11: Cho tam giác ABC có góc B, góc C đều là góc nhọn. Nêu cách vẽ hình chữ nhật DEFG có đỉnh D, đỉnh E thuộc cạnh BC, đỉnh F, đỉnh G thuộc cạnh AC, AB và có EF = 2DE.

Trả lời

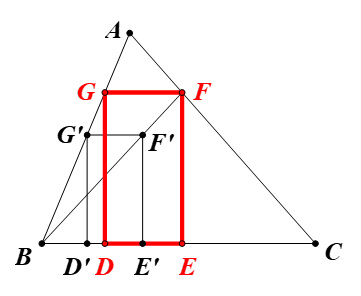
⦁ Phân tích:

Lấy điểm G’ bất kì trên AB.

Dựng hình chữ nhật D’E’F’G’ có E’F’ = 2D’E’ và hai đỉnh D’, E’ thuộc BC.

Đường thẳng BF’ cắt AC tại F.

Do D’E’F’G’ là hình chữ nhật nên G’D’ ⊥ D’E’ hay G’D’ ⊥ BC.

Mà GD ⊥ BC (do DEFG là hình chữ nhật).

Nên G’D’ // GD.

Chứng minh tương tự, ta được E’F’ // EF.

Vì D’E’F’G’ là hình chữ nhật nên G’F’ // D’E’ hay G’F’ // BC.

Mà GF // BC (do DEFG là hình chữ nhật).

Suy ra GF // G’F’.

Áp dụng định lí Thales, ta được $\frac{\mathrm{BG}}{{\mathrm{BG}}^{\text{'}}}=\frac{\mathrm{BF}}{{\mathrm{BF}}^{\text{'}}}$.

Suy ra ${\mathrm{BF}}^{\text{'}}=\frac{{\mathrm{BG}}^{\text{'}}}{\mathrm{BG}}.\mathrm{BF}$.

Mà $\overrightarrow{{\mathrm{BF}}^{\text{'}}},\overrightarrow{\mathrm{BF}}$ cùng hướng.

Do đó $\overrightarrow{{\mathrm{BF}}^{\text{'}}}=\frac{{\mathrm{BG}}^{\text{'}}}{\mathrm{BG}}.\overrightarrow{\mathrm{BF}}$.

Vì vậy ${\text{F}}^{\text{'}}=V_{\left(B,\frac{{\mathrm{BG}}^{\text{'}}}{\mathrm{BG}}\right)}\left(F\right)$ (1)

Chứng minh tương tự, ta được $D^{\text{'}}=V_{\left(B,\frac{{\mathrm{BG}}^{\text{'}}}{\mathrm{BG}}\right)}\left(D\right)$ và $E^{\text{'}}=V_{\left(B,\frac{{\mathrm{BG}}^{\text{'}}}{\mathrm{BG}}\right)}\left(E\right)$ (2)

Lại có $G^{\text{'}}=V_{\left(B,\frac{{\mathrm{BG}}^{\text{'}}}{\mathrm{BG}}\right)}\left(G\right)$ (3)

Từ (1), (2), (3), ta thu được $V_{\left(B,\frac{{\mathrm{BG}}^{\text{'}}}{\mathrm{BG}}\right)}$ biến hình chữ nhật D’E’F’G’ thành hình chữ nhật DEFG. Từ đó, ta suy ra cách dựng hình chữ nhật DEFG.

⦁ Cách dựng:

Lấy điểm G’ tùy ý trên AB.

Dựng hình chữ nhật D’E’F’G’ có E’F’ = 2D’E’, hai đỉnh D’, E’ nằm trên BC.

Đường thẳng BF’ cắt AC tại F.

Đường thẳng qua F song song với BC cắt AB tại G.

Gọi D, E lần lượt là hình chiếu của G, F lên BC.

Vậy ta đã dựng xong hình chữ nhật DEFG.

Xem thêm các bài giải Chuyên đề Toán 11 Chân trời sáng tạo hay, chi tiết khác:

Bài 6: Phép vị tự

Bài 7: Phép đồng dạng

Bài tập cuối chuyên đề 1

Bài 1: Đồ thị

Bài 2: Đường đi Euler và đường đi Hamilton

Bài 3: Bài toán tìm đường đi ngắn nhất