Thấu kính hội tụ có thể cho ảnh thật hoặc ảnh ảo A’B’ của vật AB. Tìm phép vị tự biến AB thành A’B’ trong

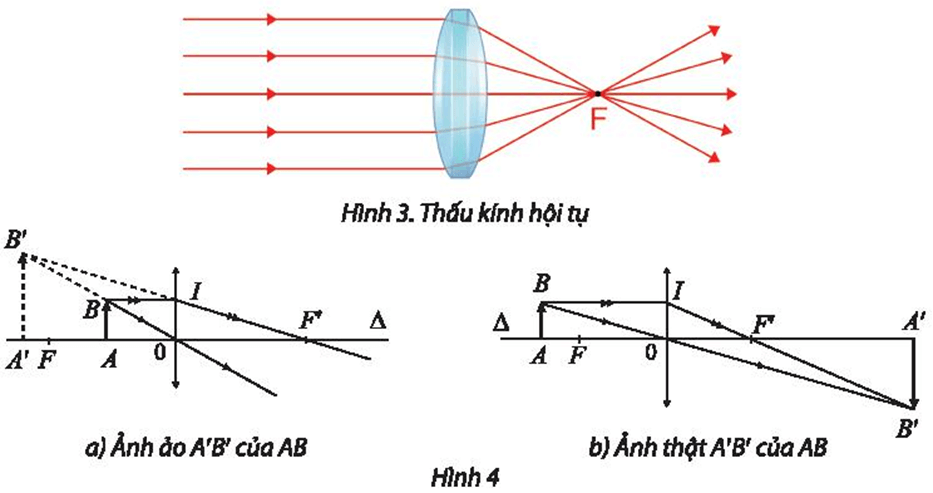
Bài 17 trang 42 Chuyên đề Toán 11: Thấu kính hội tụ có thể cho ảnh thật hoặc ảnh ảo A’B’ của vật AB. Tìm phép vị tự biến AB thành A’B’ trong Hình 3 và Hình 4.

Trả lời

⦁ Ta xét Hình 4a:

Để tìm phép vị tự biến vật AB thành ảnh A’B’, ta tìm phép vị tự biến A, B lần lượt thành A’, B’.

Ta có AA’ cắt BB’ tại O.

Vì ba điểm O, A, A’ thẳng hàng và A, A’ nằm cùng phía đối với O.

Suy ra $\overrightarrow{{\mathrm{OA}}^{\text{'}}}=k\overrightarrow{\mathrm{OA}}$, với k > 0.

Do đó V_{(O, k)}(A) = A’ và OA’ = k.OA.

Vì vậy $k=\frac{{\mathrm{OA}}^{\text{'}}}{\mathrm{OA}}$.

Xét ∆OA’B’ và ∆OAB, có:

$\widehat{\mathrm{AOB}}$ chung;

$\widehat{{\mathrm{OA}}^{\text{'}}{B}^{\text{'}}}=\widehat{\mathrm{OAB}}=90°$.

Do đó ${\mathrm{\Delta OA}}^{\text{'}}{B}^{\text{'}}\backsim \mathrm{\Delta OAB}$ (g.g).

Suy ra $\frac{{\mathrm{OB}}^{\text{'}}}{\mathrm{OB}}=\frac{{\mathrm{OA}}^{\text{'}}}{\mathrm{OA}}=k$.

Vì vậy OB’ = k.OB.

Mà ba điểm O, B, B’ thẳng hàng và B, B’ nằm cùng phía đối với O.

Suy ra $\overrightarrow{{\mathrm{OB}}^{\text{'}}}=k\overrightarrow{\mathrm{OB}}$.

Do đó V_{(O, k)}(B) = B’.

Vậy phép vị tự tâm O, tỉ số $k=\frac{{\mathrm{OA}}^{\text{'}}}{\mathrm{OA}}$ biến vật AB thành ảnh A’B’.

⦁ Ta xét Hình 4b:

Để tìm phép vị tự biến vật AB thành ảnh A’B’, ta tìm phép vị tự biến A, B lần lượt thành A’, B’.

Ta có AA’ cắt BB’ tại O.

Vì ba điểm O, A, A’ thẳng hàng và A, A’ nằm khác phía đối với O.

Suy ra $\overrightarrow{{\mathrm{OA}}^{\text{'}}}=k\overrightarrow{\mathrm{OA}}$, với k < 0.

Do đó V_{(O, k)}(A) = A’ và OA’ = |k|.OA.

Vì vậy $k=-\frac{{\mathrm{OA}}^{\text{'}}}{\mathrm{OA}}$.

Xét ∆OA’B’ và ∆OAB, có:

$\widehat{A^{\text{'}}{\mathrm{OB}}^{\text{'}}}=\widehat{\mathrm{AOB}}$ (đối đỉnh);

$\widehat{{\mathrm{OA}}^{\text{'}}{B}^{\text{'}}}=\widehat{\mathrm{OAB}}=90°$.

Do đó ${\mathrm{\Delta OA}}^{\text{'}}{B}^{\text{'}}\backsim \mathrm{\Delta OAB}$ (g.g).

Suy ra $\frac{{\mathrm{OB}}^{\text{'}}}{\mathrm{OB}}=\frac{{\mathrm{OA}}^{\text{'}}}{\mathrm{OA}}=\mathrm{|k|}$.

Vì vậy OB’ = |k|.OB.

Mà ba điểm O, B, B’ thẳng hàng và B, B’ nằm khác phía đối với O.

Suy ra $\overrightarrow{{\mathrm{OB}}^{\text{'}}}=k\overrightarrow{\mathrm{OB}}$

Do đó V_{(O, k)}(B) = B’.

Vậy phép vị tự tâm O, tỉ số $k=-\frac{{\mathrm{OA}}^{\text{'}}}{\mathrm{OA}}$ biến vật AB thành ảnh A’B’.

Xem thêm các bài giải Chuyên đề Toán 11 Chân trời sáng tạo hay, chi tiết khác:

Bài 6: Phép vị tự

Bài 7: Phép đồng dạng

Bài tập cuối chuyên đề 1

Bài 1: Đồ thị

Bài 2: Đường đi Euler và đường đi Hamilton

Bài 3: Bài toán tìm đường đi ngắn nhất