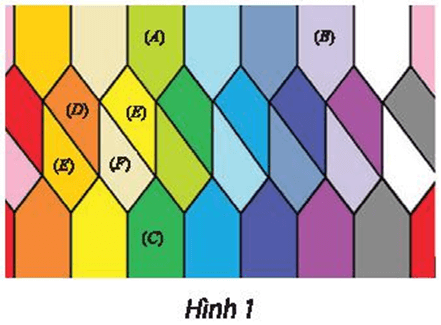
Cho Hình 1. a) Tìm phép biến hình f biến hình (A) thành hình (B). b) Tìm phép biến hình g biến hình
72
18/03/2024
Bài 15 trang 42 Chuyên đề Toán 11: Cho Hình 1.
a) Tìm phép biến hình f biến hình (A) thành hình (B).
b) Tìm phép biến hình g biến hình (A) thành hình (C).
c) Tìm các phép biến hình biến hình (D) thành lần lượt các hình (E), (F), (G).
Trả lời
a) Gọi I là một điểm trên hình (A) và I’ là một điểm trên hình (B) có vị trí tương ứng với điểm I trên hình (A) (hình vẽ).
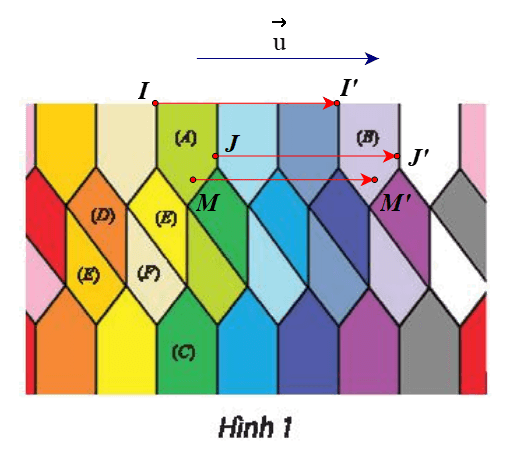
Giả sử là vectơ có phương vuông góc với trục đối xứng của hình (A), độ dài bằng độ dài từ điểm I đến điểm I’ (hình vẽ).
Tức là, .
Gọi J là một điểm bất kì trên hình (A).
Lấy điểm J’ sao cho .
Khi đó J’ là một điểm trên hình (B) có vị trí tương ứng với điểm J trên hình (A).
Tương tự như vậy, với mỗi điểm M bất kì trên hình (A), ta lấy điểm M’ sao cho thì ta được tập hợp các điểm M’ tạo thành hình (B).
Vậy phép biến hình f cần tìm là phép tịnh tiến theo .
b) Chọn đường thẳng d như hình vẽ.
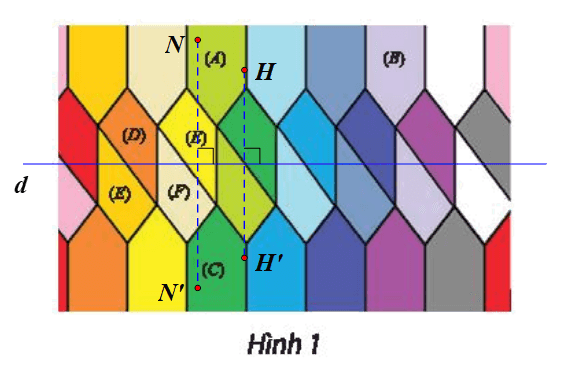
Lấy điểm H bất kì nằm trên hình (A).
Ta đặt H’ = Đd(H).
Khi đó H’ nằm trên hình (C) có vị trí tương ứng với điểm H trên hình (A).
Tương tự như vậy, với mỗi điểm N bất kì trên hình (A), ta lấy điểm N’ sao cho N’ = Đd(N) thì ta được tập hợp các điểm N’ tạo thành hình (C).
Vậy phép biến hình g cần tìm là phép đối xứng trục d, với d là đường thẳng trên Hình 1 (như hình vẽ).
c) ⦁ Phép biến hình biến hình (D) thành hình (E):
Gọi R là một điểm bất kì trên hình (D).
Giả sử O là trung điểm của cạnh bên hình thang (D) (như hình vẽ).
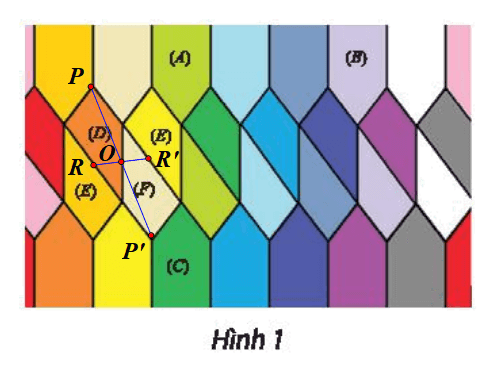
Lấy điểm R’ sao cho R’ = ĐO(R).
Khi đó R’ là một điểm trên hình (F) có vị trí tương ứng với điểm R trên hình (D).
Tương tự như vậy, với mỗi điểm P bất kì trên hình (D), ta lấy điểm P’ sao cho P’ = ĐO(P) thì ta được tập hợp các điểm P’ tạo thành hình (F).
Vậy phép đối xứng tâm O biến hình (D) thành hình (F).
⦁ Phép biến hình biến hình (D) thành hình (G):
Xem thêm các bài giải Chuyên đề Toán 11 Chân trời sáng tạo hay, chi tiết khác:
Bài 6: Phép vị tự
Bài 7: Phép đồng dạng
Bài tập cuối chuyên đề 1
Bài 1: Đồ thị
Bài 2: Đường đi Euler và đường đi Hamilton
Bài 3: Bài toán tìm đường đi ngắn nhất




