Giải Chuyên đề Toán 11 Bài 1 (Chân trời sáng tạo): Hình biểu diễn của một hình, khối

Giải Chuyên đề Toán 11 Bài 1: Hình biểu diễn của một hình, khối

Khởi động trang 70 Chuyên đề Toán 11: Trong thực tế, người ta thường phải biểu diễn các vật thể lên mặt giấy để mô tả, giải thích, diễn đạt ý tưởng thiết kế cho người thi công. Trong hai hình biểu diễn của khối lập phương dưới đây:

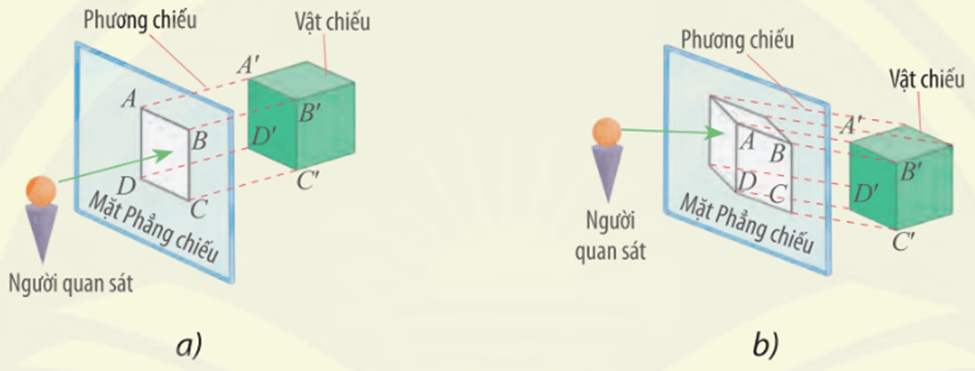
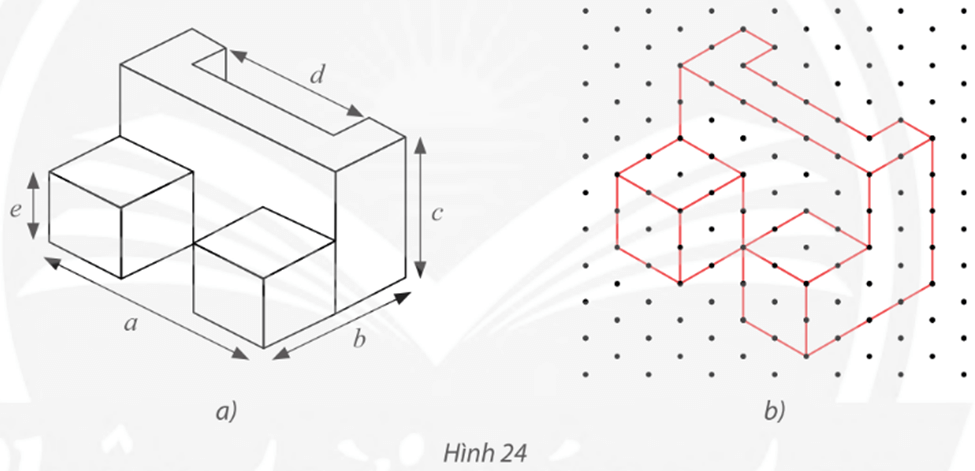
– Hình nào giúp người thi công dễ hình dung được vật thật trong không gian?

– Hình nào giúp người thi công biết được kích thước một mặt của vật thật?

Lời giải:

– Hình b) giúp người thi công dễ hình dung được vật thật trong không gian.

– Hình a) giúp người thi công biết được kích thước một mặt của vật thật.

1. Phép chiếu và hình biểu diễn

Khám phá 1 trang 70 Chuyên đề Toán 11: Hình 1 thể hiện hai cách chiếu hình ℋ thành hình ℋ ’ lên mặt phẳng (P). Mô tả cách vẽ các đỉnh của hình chiếu ℋ ’ trong mỗi trường hợp.

Lời giải:

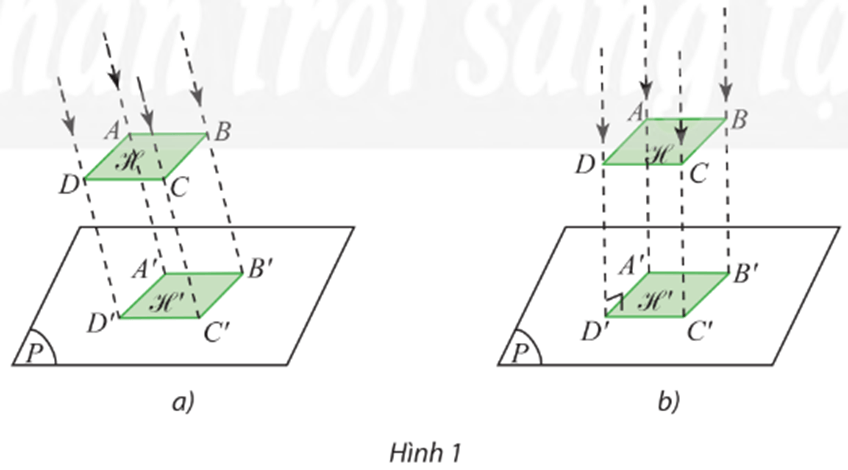
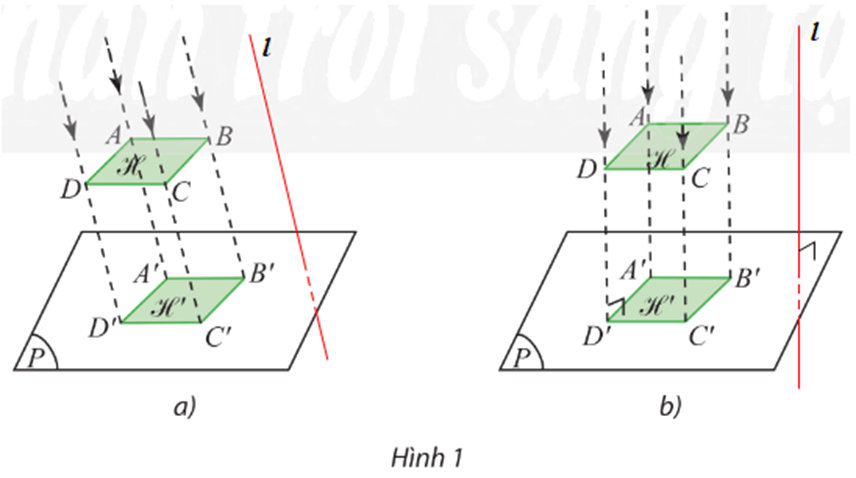
⦁ Hình 1a:

Trong không gian, vẽ đường thẳng ℓ bất kì sao cho ℓ cắt (P) (hình vẽ).

Với điểm A trong không gian, vẽ một đường thẳng đi qua A và song song (hoặc trùng) với ℓ. Đường thẳng này cắt (P) tại A’.

Vẽ tương tự như trên cho các điểm B, C, D: với các điểm B, C, D trong không gian, vẽ các đường thẳng lần lượt đi qua các điểm B, C, D và song song (hoặc trùng) với ℓ. Các đường thẳng này lần lượt cắt (P) tại B’, C’, D’.

⦁ Hình 1b:

Trong không gian, vẽ đường thẳng ℓ bất kì sao cho ℓ vuông góc với (P) (hình vẽ).

Với điểm A trong không gian, vẽ một đường thẳng đi qua A và song song (hoặc trùng) với ℓ. Đường thẳng này cắt (P) tại A’.

Vẽ tương tự như trên cho các điểm B, C, D: với các điểm B, C, D trong không gian, vẽ các đường thẳng lần lượt đi qua các điểm B, C, D và song song (hoặc trùng) với ℓ. Các đường thẳng này lần lượt cắt (P) tại B’, C’, D’.

Thực hành 1 trang 72 Chuyên đề Toán 11: Dưới đây là ba hình biểu diễn của hình trụ có độ dài đường kính đáy bằng 10 cm và chiều cao bằng 12 cm. Chỉ ra phép chiếu được sử dụng tương ứng với mỗi hình.

Lời giải:

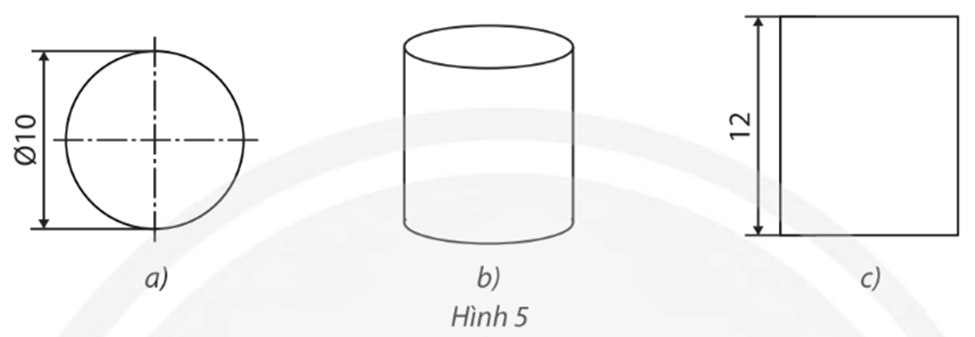
– Hình 5a là hình tròn có độ dài đường kính đáy bằng 10 cm nên nó là hình chiếu của hình trụ qua phép chiếu vuông góc có mặt phẳng chiếu song song với mặt đáy của hình trụ.

– Phép chiếu được sử dụng ở Hình 5b là phép chiếu song song.

– Hình 5c là hình chữ nhật có chiều dài bằng 12 cm (bằng chiều cao của hình trụ) nên nó là hình chiếu của hình trụ qua phép chiếu vuông góc có mặt phẳng chiếu song song với đường sinh của hình trụ.

Vận dụng 1 trang 72 Chuyên đề Toán 11: Phép chiếu nào được sử dụng để vẽ các hình biểu diễn của bàn làm việc trong Hình 6?

Lời giải:

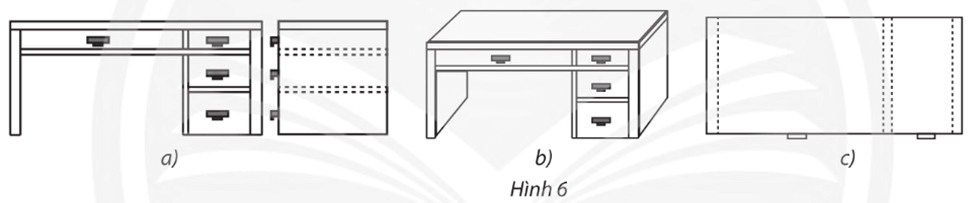
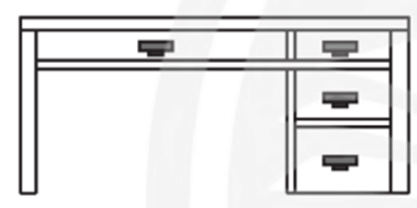
– Hình 6a:

Phép chiếu được sử dụng ở hình vẽ trên là phép chiếu vuông góc có mặt phẳng chiếu song song với mặt trước của bàn làm việc.

Phép chiếu được sử dụng ở hình vẽ trên là phép chiếu vuông góc có mặt phẳng chiếu song song với mặt bên của bàn làm việc.

– Hình 6b:

Phép chiếu được sử dụng ở Hình 6b là phép chiếu song song.

– Hình 6c:

Phép chiếu được sử dụng ở Hình 6c là phép chiếu vuông góc có mặt phẳng chiếu song song với mặt bàn của bàn làm việc.

2. Phương pháp chiếu vuông góc

Khám phá 2 trang 72 Chuyên đề Toán 11: Trong Hình 7, theo em, nếu chỉ dùng một hình chiếu vuông góc của hình hộp chữ nhật ℋ trên một trong ba mặt phẳng đôi một vuông góc (P₁), (P₂), (P₃) có đủ để chế tạo được ℋ không?

Lời giải:

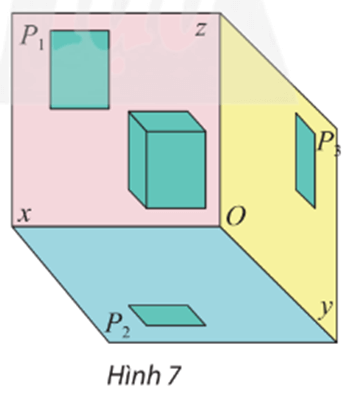
Ta thấy nếu chỉ dùng một hình chiếu vuông góc của hình hộp chữ nhật ℋ trên một trong ba mặt phẳng đôi một vuông góc (P₁), (P₂), (P₃) trong Hình 7 thì hình chiếu đó chỉ thể hiện được một mặt của vật thật dẫn đến chế tạo không chính xác.

Vậy nếu chỉ dùng một hình chiếu vuông góc của hình hộp chữ nhật ℋ trên một trong ba mặt phẳng đôi một vuông góc (P₁), (P₂), (P₃) thì không đủ để chế tạo được hình ℋ.

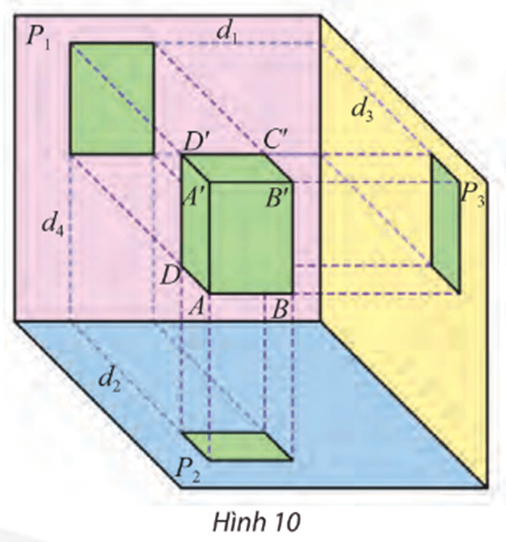
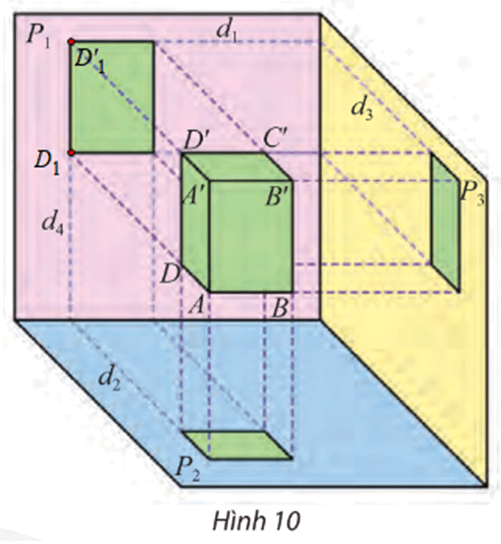
Khám phá 3 trang 74 Chuyên đề Toán 11: Quan sát Hình 10 và cho biết:

– Trong ba cạnh AB, AA’ và AD của hình hộp chữ nhật, cạnh nào song song với một trong ba mặt phẳng chiếu (P₁), (P₂), (P₃)?

– Tìm hai giao tuyến của (P₁) và (P₂) với mặt phẳng đi qua điểm D và vuông góc với cả (P₁) và (P₂).

Lời giải:

– Trong ba cạnh AB, AA’ và AD của hình hộp chữ nhật ABCD.A’B’C’D’, ta có:

⦁ Cạnh AB song song với các mặt phẳng chiếu (P₁) và (P₂);

⦁ Cạnh AA’ song song với các mặt phẳng chiếu (P₁) và (P₃);

⦁ Cạnh AD song song với các mặt phẳng chiếu (P₂) và (P₃).

Vậy cả ba cạnh AB, AA’ và AD của hình hộp chữ nhật đều song song với một trong ba mặt phẳng chiếu (P₁), (P₂) và (P₃).

– Xác định hai giao tuyến của (P₁) và (P₂) với mặt phẳng đi qua điểm D và vuông góc với cả (P₁) và (P₂):

Ta có AD ⊥ AA’ (do ABCD.A’B’C’D’ là hình hộp chữ nhật).

Mà AA’ // (P₁).

Suy ra AD ⊥ (P₁).

Do đó (AA’D’D) ⊥ (P₁).

Chứng minh tương tự, ta được (AA’D’D) ⊥ (P₂).

Vì vậy mặt phẳng đi qua điểm D và vuông góc với cả (P₁) và (P₂) là (AA’D’D).

Gọi D₁, D₁’ lần lượt là hình chiếu vuông góc của các điểm D, D’ lên mặt phẳng (P₁).

Suy ra D₁, D₁’∈ (AA’D’D) và D₁, D₁’∈ (P₁).

Do đó hay d₄ = (AA’D’D) ∩ (P₁).

Chứng minh tương tự, ta được d₂ = (AA’D’D) ∩ (P₂).

Vậy d₄, d₂ lần lượt là hai giao tuyến cần tìm.

Thực hành 2 trang 75 Chuyên đề Toán 11:

a) Trên Hình 10, độ dài cạnh AD được bảo toàn trên các hình chiếu nào của bản vẽ? Tại sao?

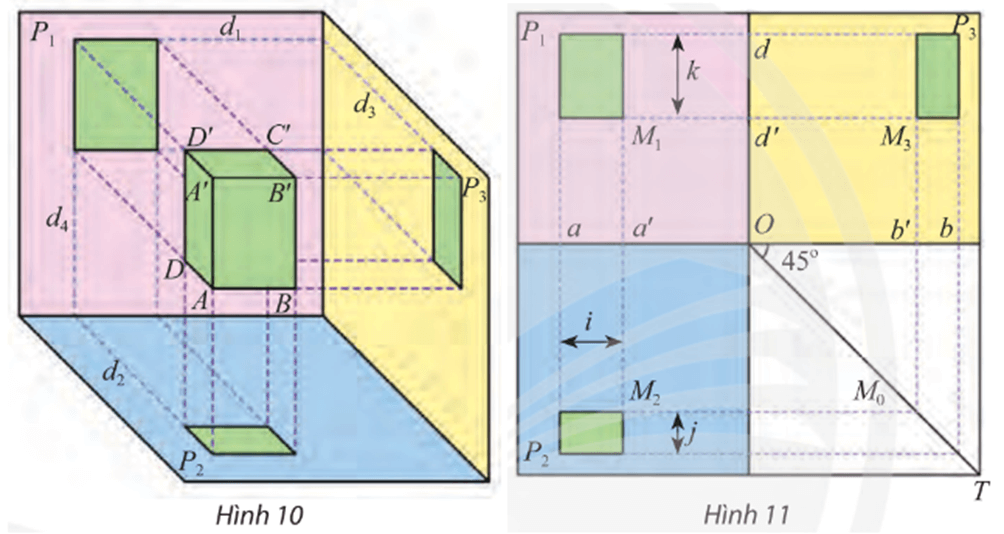
b) Trên Hình 11, tìm hai giao tuyến được biểu diễn thành đường gióng a trên bản vẽ.

c) Trên Hình 11, khoảng cách giữa hai đường gióng nào cho ta chiều cao AA’ của vật ở Hình 10?

Lời giải:

a) Trên Hình 10, độ dài cạnh AD được bảo toàn trên hình chiếu bằng và hình chiếu cạnh của bản vẽ vì AD song song với (P₂) và (P₃).

b) Hai giao tuyến được biểu diễn thành đường gióng a trên Hình 11 là d₄ và d₂.

c) Trên Hình 11, ta thấy độ dài mũi tên k bằng chiều cao AA’ của vật ở Hình 10.

Vậy trên Hình 11, khoảng cách giữa hai đường gióng d và d’ cho ta chiều cao AA’ của vật ở Hình 10.

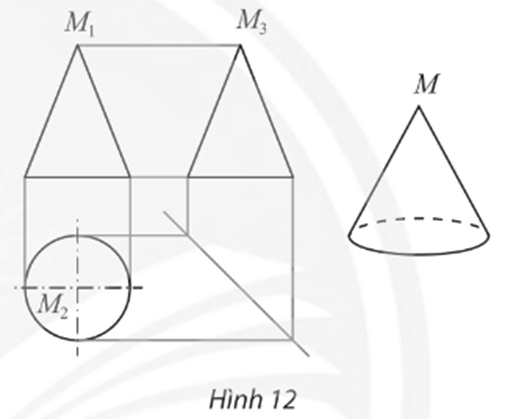
Vận dụng 2 trang 75 Chuyên đề Toán 11: Trong bản vẽ biểu diễn hình nón trong Hình 12.

a) Khoảng cách giữa hai đường gióng nào cho ta biết chiều cao của hình nón?

b) Khoảng cách giữa hai đường gióng nào cho ta biết độ dài đường kính đáy của hình nón?

c) Nêu cách xác định điểm M₃ biểu diễn đỉnh M của hình nón trong hình chiếu cạnh khi biết hai điểm M₁ và M₂ biểu diễn M trong hình chiếu đứng và hình chiếu bằng.

Lời giải:

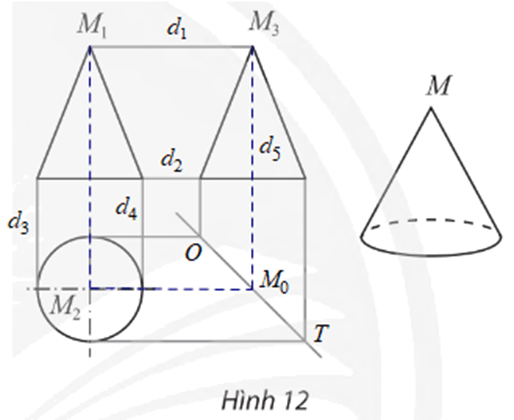
Gọi d₁, d₂, d₃, d₄, d₅ là các đường gióng của bản vẽ (như hình vẽ).

a) Khoảng cách giữa hai đường gióng d₁ và d₂ cho ta biết chiều cao của hình nón.

b) Khoảng cách giữa hai đường gióng d₃ và d₄ cho ta biết độ dài đường kính đáy của hình nón.

c) Gọi OT là đường phân giác của bản vẽ (như hình vẽ).

– Phác họa đường gióng qua M₂ và song song với d₁, đường gióng này cắt OT tại M₀.

– Phác họa đường gióng d₅ qua M₀ và song song với M₁M₂.

Giao điểm của d₅ và d₁ là điểm M₃ cần tìm.

2. Phương pháp chiếu trục đo

Khám phá 4 trang 75 Chuyên đề Toán 11: Cho hình hộp chữ nhật OABC.O₁A₁B₁C₁. Ba tia Ox, Oy, Oz lần lượt chứa ba cạnh OA, OC, OO₁. Cho mặt phẳng (P) và đường thẳng l không song song với (P). Tìm ảnh của hình hộp chữ nhật OABC.O₁A₁B₁C₁ và ảnh của các tia Ox, Oy, Oz qua phép chiếu song song theo phương l lên mặt phẳng (P).

Lời giải:

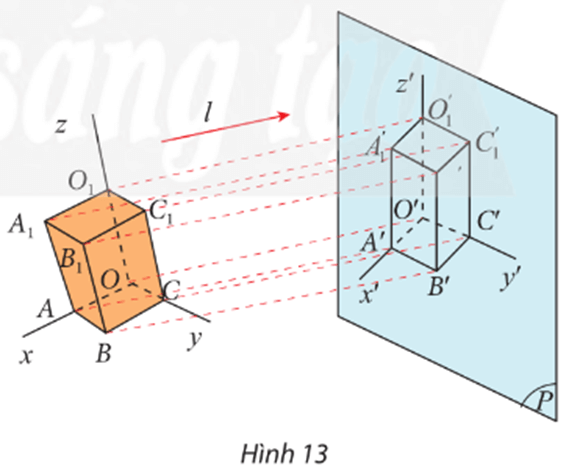
– Ta có OO’ // l và O’ ∈ (P).

Suy ra O’ là ảnh của O qua phép chiếu song song theo phương l lên mặt phẳng (P).

Chứng minh tương tự, ta được A’, B’, C’, lần lượt là ảnh của A, B, C, O₁, A₁, B₁, C₁ qua phép chiếu song song theo phương l lên mặt phẳng (P).

Do đó là ảnh của hình hộp chữ nhật OABC.O₁A₁B₁C₁ qua phép chiếu song song theo phương l lên mặt phẳng (P).

– Ta có O’, A’ lần lượt là ảnh của O, A qua phép chiếu song song theo phương l lên mặt phẳng (P).

Suy ra O’A’ là ảnh của OA qua phép chiếu song song theo phương l lên mặt phẳng (P).

Mà A’ ∈ O’x’.

Do đó O’x’ là ảnh của Ox qua phép chiếu song song theo phương l lên mặt phẳng (P).

Chứng minh tương tự, ta được O’y’, O’z’ lần lượt là ảnh của Oy, Oz qua phép chiếu song song theo phương l lên mặt phẳng (P).

Vậy ảnh của hình hộp chữ nhật OABC.O₁A₁B₁C₁ và ảnh của các tia Ox, Oy, Oz qua phép chiếu song song theo phương l lên mặt phẳng (P) lần lượt là hình hộp chữ nhật và các tia O’x’, O’y’, O’z’.

Khám phá 5 trang 76 Chuyên đề Toán 11: Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng đơn vị (Hình 14).

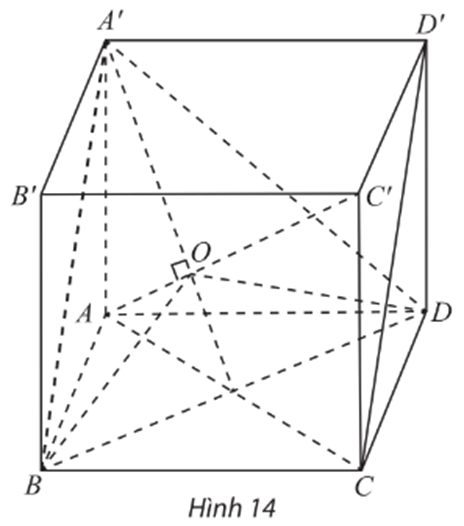
a) Chỉ ra rằng AC’ ⊥ (A’BD).

b) Gọi O là tâm của tam giác đều A’BD. Hình chiếu vuông góc của ba đoạn AB, AD và AA’ lên (A’BD) có bằng nhau không?

c) Chỉ ra rằng $\widehat{\mathrm{BOD}}=\widehat{{\mathrm{DOA}}^{\text{'}}}=\widehat{A^{\text{'}}\mathrm{OB}}=120°$.

Lời giải:

a) Ta có A’D ⊥ AD’ (AA’D’D là hình vuông) và A’D ⊥ C’D’ (C’D’ ⊥ (AA’D’D)).

Suy ra A’D ⊥ (AC’D’).

Do đó A’D ⊥ AC’ (1)

Chứng minh tương tự, ta được A’B ⊥ AC’ (2)

Từ (1), (2), ta thu được AC’ ⊥ (A’BD).

b) Gọi M là trung điểm BD.

Ta có AB = AD (do ABCD là hình vuông).

Suy ra tam giác ABD cân tại A.

Do đó AM ⊥ BD.

Lại có O là tâm của tam giác đều A’BD.

Suy ra A’M ⊥ BD và O ∈ A’M.

Ta có AM ⊥ BD và A’M ⊥ BD (chứng minh trên).

Suy ra BD ⊥ (AA’M).

Do đó BD ⊥ AO (3)

Chứng minh tương tự, ta được A’D ⊥ AO (4)

Từ (3), (4), suy ra AO ⊥ (A’BD).

Khi đó O là hình chiếu vuông góc của A lên mặt phẳng (A’BD).

Mà B là hình chiếu vuông góc của B lên mặt phẳng (A’BD).

Suy ra OB là hình chiếu vuông góc của AB lên mặt phẳng (A’BD).

Chứng minh tương tự, ta được: OD, OA’ lần lượt là hình chiếu vuông góc của AD, AA’ lên mặt phẳng (A’BD).

Tam giác A’BD đều có tâm O.

Suy ra OA’ = OB = OD.

Vậy hình chiếu vuông góc OB, OD và OA’ lần lượt của ba đoạn AB, AD và AA’ lên (A’BD) có độ dài bằng nhau.

c) Ta có tam giác A’BD đều. Suy ra $\widehat{{\mathrm{BA}}^{\text{'}}D}=60°$.

Tam giác A’BD đều có tâm O. Suy ra O là tâm đường tròn ngoại tiếp tam giác A’BD.

Khi đó $\widehat{\mathrm{BOD}}=2\widehat{{\mathrm{BA}}^{\text{'}}D}=2.60°=120°$.

Chứng minh tương tự, ta được $\widehat{{\mathrm{DOA}}^{\text{'}}}=120°$ và $\widehat{A^{\text{'}}\mathrm{OB}}=120°$.

Vậy $\widehat{\mathrm{BOD}}=\widehat{{\mathrm{DOA}}^{\text{'}}}=\widehat{A^{\text{'}}\mathrm{OB}}=120°$.

Thực hành 3 trang 79 Chuyên đề Toán 11: Vẽ trên giấy kẻ ô li hình biểu diễn của hình lăng trụ đứng có đáy là tam giác vuông với các kích thước được cho như trong Hình 23 (quy tắc mỗi cạnh của tam giác đều biểu diễn độ dài 1 cm).

Lời giải:

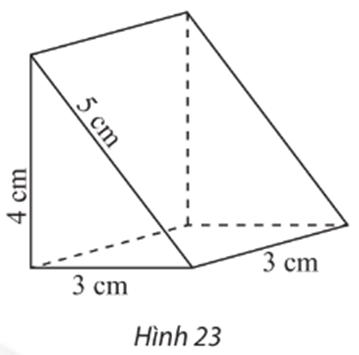
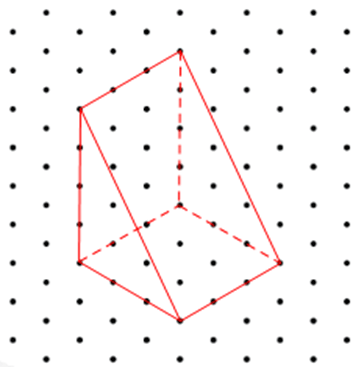
Hình biểu diễn của hình lăng trụ đứng có đáy là tam giác vuông với các kích thước được cho như trong Hình 23 là:

Vận dụng 3 trang 79 Chuyên đề Toán 11: Tìm các kích thước a, b, c, d, e của chi tiết cơ khí trong Hình 24a có hình biểu diễn được vẽ trên giấy kẻ ô li là Hình 24b với quy ước mỗi cạnh của tam giác đều biểu diễn độ dài 1 cm.

Lời giải:

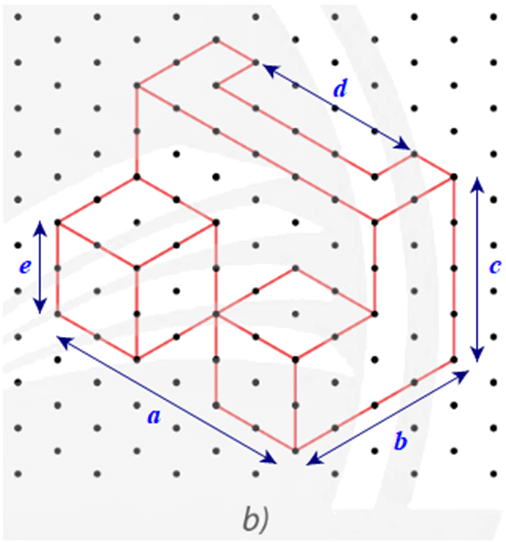
Các kích thước a, b, c, d, e của chi tiết cơ khí trong Hình 24a được biểu diễn trên Hình 24b như sau:

Do mỗi cạnh của tam giác đều biểu diễn độ dài 1 cm nên ta có:

Chiều dài a = 6 cm; chiều rộng b = 4 cm; chiều cao c = 4 cm; bề dày d = 4 cm; bề dày e = 2 cm.

Bài tập

Bài 1 trang 79 Chuyên đề Toán 11: Phác họa hình chiếu vuông góc của:

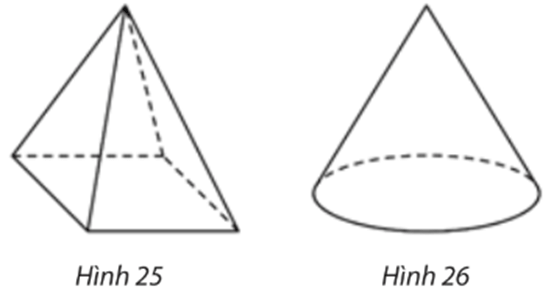
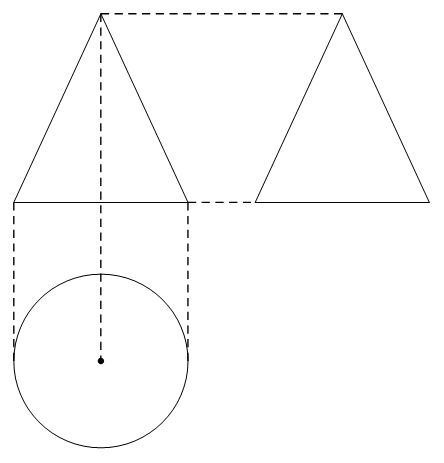
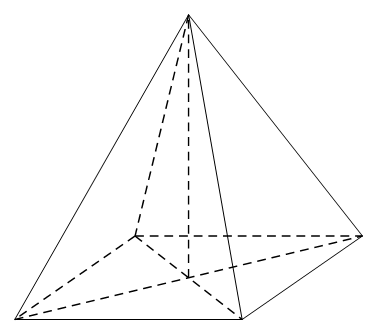
a) Khối chóp tứ giác đều (Hình 25).

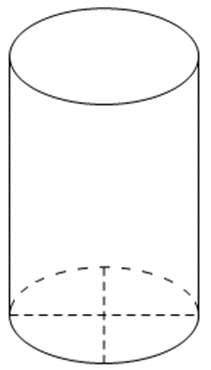
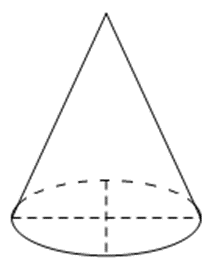
b) Khối nón tròn xoay (Hình 26).

Lời giải:

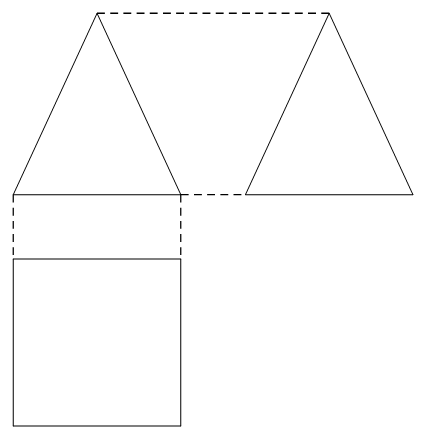
a) Hình chiếu vuông góc của khối chóp tứ giác đều ở Hình 25 được biểu diễn trên bản vẽ như sau:

b) Hình chiếu vuông góc của khối nón tròn xoay ở Hình 26 được biểu diễn trên bản vẽ như sau:

Bài 2 trang 80 Chuyên đề Toán 11: Mô tả vật thể trong không gian có hai hình chiếu vuông góc trong Hình 27.

Lời giải:

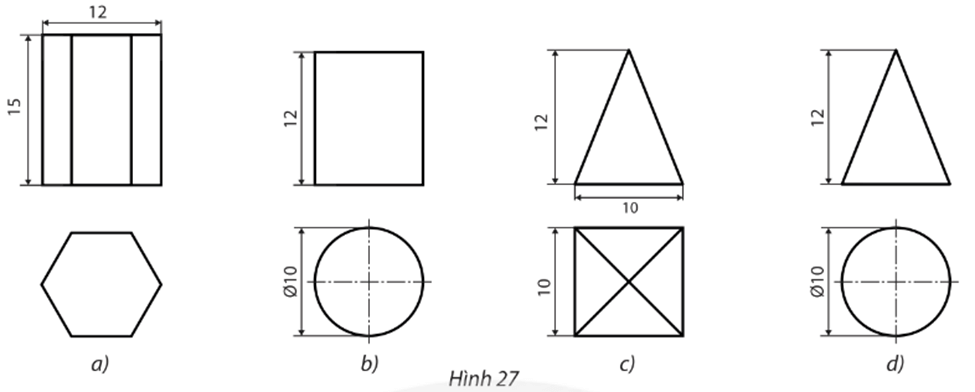
Trong các Hình 27a, b, c, d, ta đã có hình chiếu đứng và hình chiếu bằng của vật thể được biểu diễn ở mỗi hình. Do đó ta có thể mô tả vật thể trong không gian như sau:

– Hình 27a là khối lăng trụ đứng có đáy là lục giác đều, trong đó chiều cao bằng 15 cm, độ dài cạnh đáy là $\frac{12}{2}=6$ cm.

– Hình 27b là khối trụ có độ dài đường kính đáy bằng 10 cm, chiều cao bằng 12 cm.

– Hình 27c là khối chóp tứ giác đều có cạnh của hình vuông bằng 10, chiều cao của khối chóp bằng 12.

– Hình 27d là khối nón tròn xoay có độ dài đường kính đáy bằng 10 cm, chiều cao bằng 12 cm.

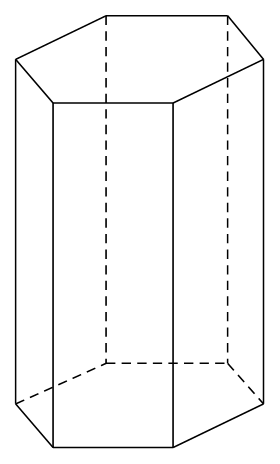
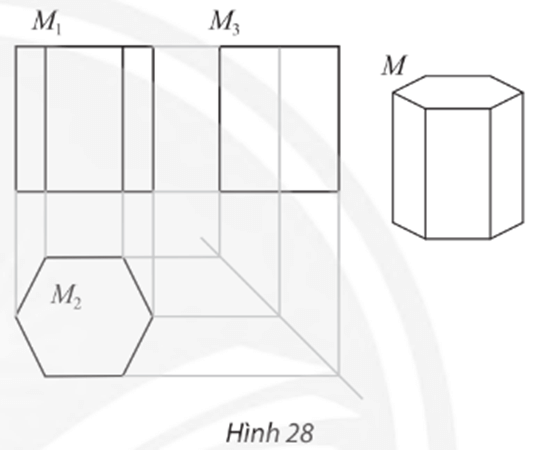
Bài 3 trang 80 Chuyên đề Toán 11: Trong bản vẽ biểu diễn hình lăng trụ lục giác đều trong Hình 28.

a) Khoảng cách giữa hai đường gióng nào cho ta biết chiều cao của lăng trụ?

b) Khoảng cách giữa hai đường gióng nào cho ta biết độ dài cạnh đáy của lăng trụ?

c) Nêu cách xác định điểm M₃ biểu diễn đỉnh M của đáy trên của lăng trụ khi biết M₁ và M₂ biểu diễn M trong hình chiếu đứng và hình chiếu bằng.

Lời giải:

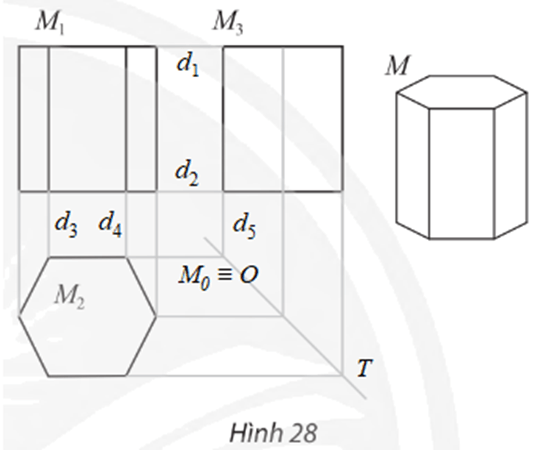
Gọi d₁, d₂, d₃, d₄, d₅ là các đường gióng của bản vẽ (như hình vẽ).

a) Khoảng cách giữa hai đường gióng d₁ và d₂ cho ta biết chiều cao của lăng trụ.

b) Khoảng cách giữa hai đường gióng d₃ và d₄ cho ta biết độ dài cạnh đáy của lăng trụ.

c) Gọi OT là đường phân giác của bản vẽ (hình vẽ).

– Phác họa đường gióng qua M₂ và song song với d₁, đường gióng này cắt OT tại M₀ ≡ O.

– Phác họa đường gióng d₅ qua M₀ và song song với M₁M₂.

Giao điểm của d₅ và d₁ là điểm M₃ cần tìm.

Bài 4 trang 80 Chuyên đề Toán 11: Vẽ hình chiếu vuông góc của các hình sau:

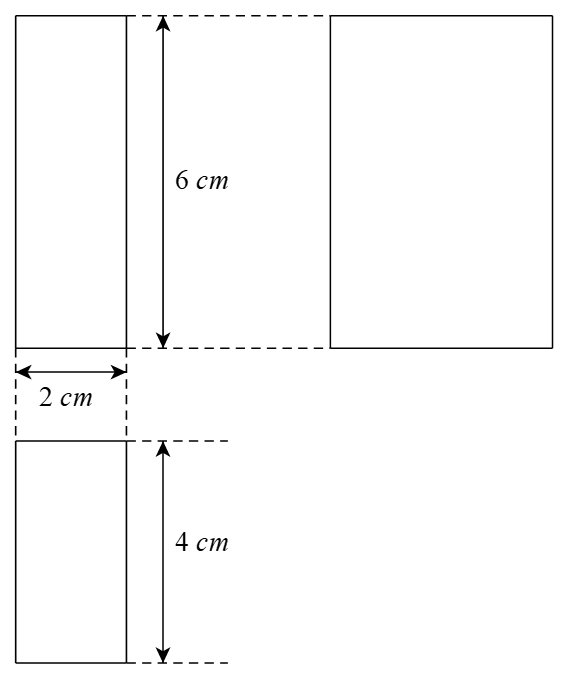
a) Hình hộp chữ nhật có ba kích thước 2 cm; 4 cm; 6 cm.

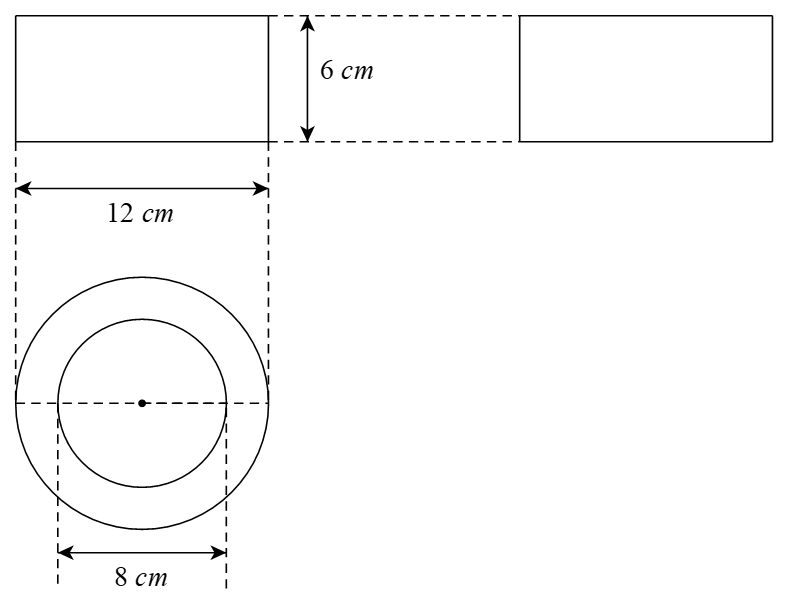
b) Hình trụ rỗng tròn xoay có chiều cao 6 cm và bán kính đáy ngoài 6 cm, bán kính đáy trong 4 cm.

Lời giải:

a) Hình chiếu vuông góc của hình hộp chữ nhật có ba kích thước 2 cm; 4 cm; 6 cm là:

b) Hình trụ rỗng tròn xoay có bán kính đáy ngoài 6 cm và bán kính đáy trong 4 cm.

Suy ra hình trụ rỗng tròn xoay có đường kính ngoài 12 cm và đường kính trong 8 cm.

Hình chiếu vuông góc của hình trụ rỗng tròn xoay có chiều cao 6 cm và bán kính đáy ngoài 6 cm, bán kính đáy trong 4 cm là:

Bài 5 trang 80 Chuyên đề Toán 11: Dùng giấy kẻ ô li với quy ước mỗi cạnh của tam giác đều biểu diễn độ dài 1 cm, vẽ hình biểu diễn của chi tiết cơ khí có hình dạng và các kích thước như trong Hình 29.

Lời giải:

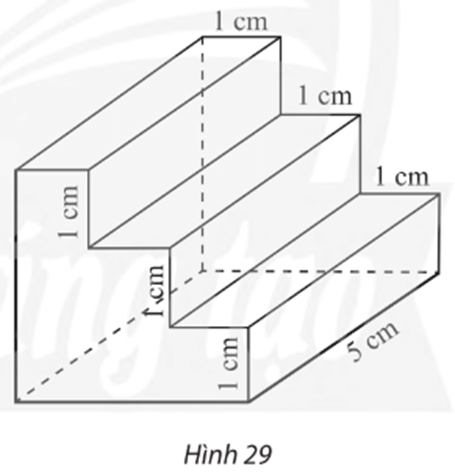
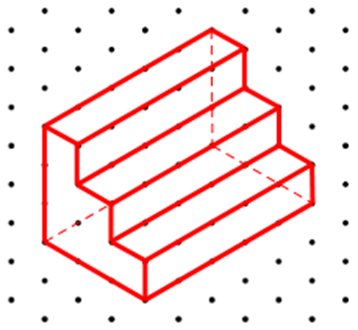
Hình biểu diễn của chi tiết cơ khí có hình dạng và các kích thước như trong Hình 29 là:

Bài 6 trang 80 Chuyên đề Toán 11: Tìm các kích thước a, b, c, d, e của chi tiết cơ khí trong Hình 30a có hình biểu diễn được vẽ trên giấy kẻ ô li trên Hình 30b với quy ước mỗi cạnh của tam giác đều biểu diễn độ dài 10 mm.

Lời giải:

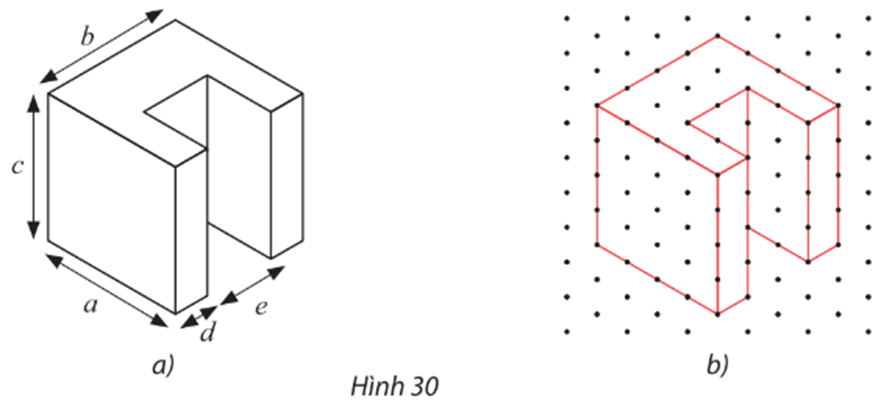
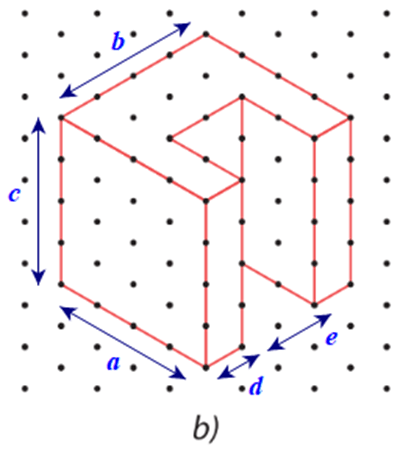
Các kích thước a, b, c, d, e của chi tiết cơ khí trong Hình 30a được biểu diễn trên Hình 30b như sau:

Do mỗi cạnh của tam giác đều biểu diễn độ dài 10 mm nên ta có:

Chiều dài a = 4.10 = 40 mm; chiều rộng b = 4.10 = 40 mm; chiều cao c = 4.10 = 40 mm; bề dày d = 1.10 = 10 mm; bề dày e = 2.10 = 20 mm.

Xem thêm các bài giải Chuyên đề học tập Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác:

Bài 2: Đường đi Euler và đường đi Hamilton

Bài 3: Bài toán tìm đường đi ngắn nhất

Bài tập cuối chuyên đề 2

Bài 2: Bản vẽ kĩ thuật

Bài tập cuối chuyên đề 3