Xét vị trí tương đối của các cặp đường thẳng d1 và d2 trong các trường hợp sau
618
13/06/2023
Thực hành 4 trang 53 Toán lớp 10 Tập 2: Xét vị trí tương đối của các cặp đường thẳng d1 và d2 trong các trường hợp sau:
a) d1: x – 5y + 9 = 0 và d2: 10x + 2y + 7 = 10;
b) 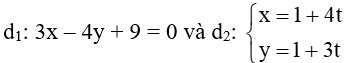
c) 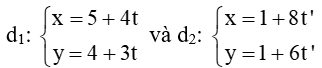
Trả lời
a) Ta có d1 và d2 có vectơ pháp tuyến lần lượt là →n1(1; -5) và →n2(10; 2)
Ta lại có: →n1.→n2 = a1a2 – b1b2 = 1.10 + 2.(-5) = 0, suy ra →n1 ⊥ →n2 .
Do đó d1 và d2 là hai đường thẳng vuông góc với nhau.
b) Vec tơ chỉ phương của d2 là →u2(4;3)
Khi đó vectơ pháp tuyến của đường thẳng d2 là →n2(-3; 4).
Vectơ pháp tuyến của đường thẳng d1 là →n1(3; -4).
Ta có: a1b2 – b1a2 = (-3).(-4) – 3.4 = 0. Suy ra hai vectơ →n1 và →n2 cùng phương.
Do đó hai đường thẳng d1 và d2 song song hoặc trùng nhau.
Lấy điểm M(1; 1) thuộc đường thẳng d2, thay tọa độ của M vào phương trình đường thẳng d1 ta được: 3.1 – 4.1 + 9 = 8 ≠ 0, suy ra M không thuộc d1.
Vậy hai đường thẳng d1 và d2 song song.
c) Đường thẳng d1 và d2 lần lượt có vec tơ chỉ phương là →u1(4; 3) và →u2(8; 6).
Ta có: a1b2 – b1a2 = 4.6 – 3.8 = 24 – 24 = 0. Suy ra hai vectơ →u1 và →u2 cùng phương.
Do đó hai đường thẳng d1 và d2 song song hoặc trùng nhau.
Lấy điểm M(1; 1) thuộc đường thẳng d2, thay tọa độ của M vào phương trình đường thẳng d1 ta được: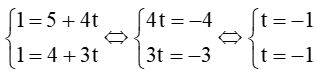 , suy ra M thuộc d1.
, suy ra M thuộc d1.
Vậy hai đường thẳng d1 và d2 trùng nhau.
Xem thêm lời giải bài tập SGK Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Bài tập cuối chương 8
Bài 1: Toạ độ của vectơ
Bài 2: Đường thẳng trong mặt phẳng toạ độ
Bài 3: Đường tròn trong mặt phẳng toạ độ
Bài 4: Ba đường conic trong mặt phẳng tọa độ
Bài tập cuối chương 9

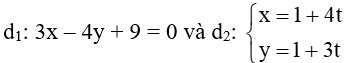
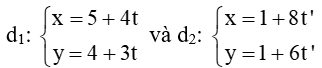
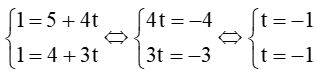 , suy ra M thuộc d1.
, suy ra M thuộc d1.