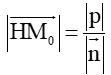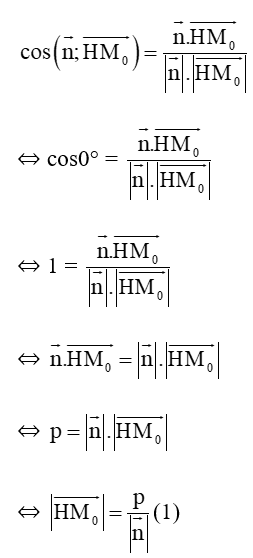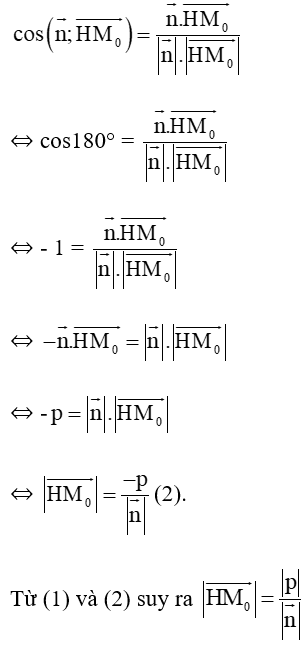Trong mặt phẳng Oxy, cho đường thẳng ∆: ax + by + c = 0 (a^2 + b^2 > 0) có vectơ pháp tuyến n

Hoạt động khám phá 7 trang 56 Toán lớp 10 Tập 2: Trong mặt phẳng Oxy, cho đường thẳng ∆: ax + by + c = 0 (a² + b² > 0) có vectơ pháp tuyến $\overrightarrow{n}$ và cho điểm M₀(x₀; y₀) có hình chiếu vuông góc H(x_H; y_H) trên ∆ (Hình 9).

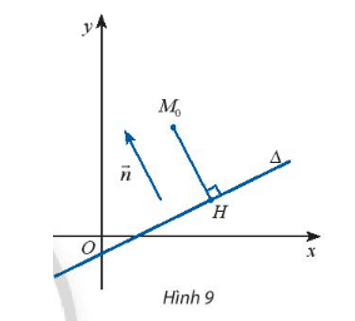
a) Chứng minh rằng hai vectơ $\overrightarrow{n}$ và $\overrightarrow{H{M}_0}$ cùng phương và tìm tọa độ của chúng.

b) Gọi p là tích vô hướng của hai vectơ $\overrightarrow{n}$ và $\overrightarrow{H{M}_0}$. Chứng minh rằng p = ax₀ + by₀ + c.

c) Giải thích công thức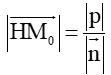 

Trả lời

a) Do $\overrightarrow{n}$ là vectơ pháp tuyến của ∆ nên $\overrightarrow{n}$⊥∆.

Ta lại có H là hình chiếu của M trên đường thẳng ∆ nên MH ⊥∆.

Suy ra $\overrightarrow{n}$// $\overrightarrow{H{M}_0}$(cùng vuông góc với ∆)

Do đó hai vectơ $\overrightarrow{n}$và $\overrightarrow{H{M}_0}$ cùng phương.

Vì $\overrightarrow{n}$ là vectơ pháp tuyến của ∆ nên tọa độ của vectơ pháp tuyến là $\overrightarrow{n}$(a; b).

Ta có $\overrightarrow{H{M}_0}$ = (x₀ – x_H; y₀ – y_H).

b) Ta có: $\overrightarrow{n}.\overrightarrow{H{M}_0}=a\left(x_0-x_H\right)+b\left(y_0-y_H\right)$ = ax₀ – ax_H + by₀ – by_H = ax₀ + by₀ – ax_H – by_H .

Vì điểm H thuộc đường thẳng ∆ nên thay tọa độ điểm H vào phương trình ∆ ta được:

– ax_H – by_H = c ⇔ – ax_H – by_H = c.

Khi đó $\overrightarrow{n}.\overrightarrow{H{M}_0}$= ax₀ + by₀ + c với c = – ax_H – by_H.

Vậy p = ax₀ + by₀ + c.

c) Vì hai vectơ $\overrightarrow{n}$ và $\overrightarrow{H{M}_0}$ cùng phương nên góc giữa hai vectơ $\overrightarrow{n}$ và $\overrightarrow{H{M}_0}$ bằng 0° hoặc bằng 180°.

TH1. Góc giữa hai vectơ $\overrightarrow{n}$ và $\overrightarrow{H{M}_0}$ bằng 0°

Áp dụng công thức cos giữa hai vectơ ta được:

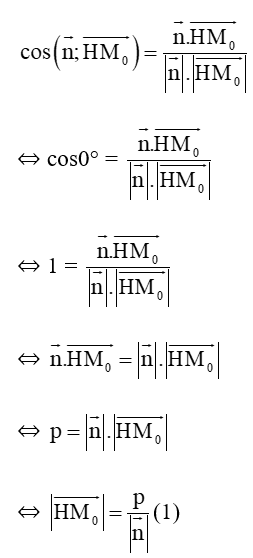
TH2. Góc giữa hai vectơ $\overrightarrow{n}$ và $\overrightarrow{H{M}_0}$ bằng 180°

Áp dụng công thức cos giữa hai vectơ ta được:

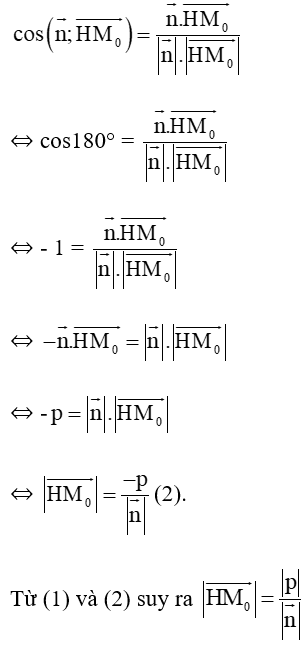
Xem thêm lời giải bài tập SGK Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Bài tập cuối chương 8

Bài 1: Toạ độ của vectơ

Bài 2: Đường thẳng trong mặt phẳng toạ độ

Bài 3: Đường tròn trong mặt phẳng toạ độ

Bài 4: Ba đường conic trong mặt phẳng tọa độ

Bài tập cuối chương 9