Tìm giá trị lớn nhất và giá trị nhỏ nhất của p a) y = sin x – cos x; b) y = sin x

Bài 1.59 trang 29 SBT Toán 11 Tập 1: Tìm giá trị lớn nhất và giá trị nhỏ nhất của p

a) y = sin x – cos x;

b) y = sin x + sin$\left(\frac{\pi }{3}-x\right)$;

c) y = sin⁴ x + cos⁴ x;

d) y = cos 2x + 2cos x – 1.

Trả lời

a) Ta có y = sin x – cos x = $\sqrt{2}\sin \left(x-\frac{\pi }{4}\right)$.

Vì $-1\le \sin \left(x-\frac{\pi }{4}\right)\le 1$ nên $-\sqrt{2}\le \sqrt{2}\sin \left(x-\frac{\pi }{4}\right)\le \sqrt{2}$, với mọi $x\in ℝ$.

Vậy giá trị lớn nhất của hàm số là $\sqrt{2}$, đạt được khi $\sin \left(x-\frac{\pi }{4}\right)=1$

$\iff x-\frac{\pi }{4}=\frac{\pi }{2}+k2\pi \left(k\in \mathbb{Z}\right)$ $\iff x=\frac{3\pi }{4}+k2\pi \left(k\in \mathbb{Z}\right)$>.

Giá trị nhỏ nhất của hàm số là $-\sqrt{2}$, đạt được khi $\sin \left(x-\frac{\pi }{4}\right)=-1$

$\iff x-\frac{\pi }{4}=-\frac{\pi }{2}+k2\pi \left(k\in \mathbb{Z}\right)$ $\iff x=-\frac{\pi }{4}+k2\pi \left(k\in \mathbb{Z}\right)$.

b) Ta có y = sin x + sin$\left(\frac{\pi }{3}-x\right)$ $=2\sin \frac{x+\frac{\pi }{3}-x}{2}\cos \frac{x-\frac{\pi }{3}+x}{2}$

$=2\sin \frac{\pi }{6}\cos \left(x-\frac{\pi }{6}\right)$$=2.\frac{1}{2}\cos \left(x-\frac{\pi }{6}\right)=\cos \left(x-\frac{\pi }{6}\right)$.

Ta có $-1\le \cos \left(x-\frac{\pi }{6}\right)\le 1\forall x\in ℝ$.

Vậy giá trị lớn nhất của hàm số là 1, đạt được khi $\cos \left(x-\frac{\pi }{6}\right)=1$$\iff x-\frac{\pi }{6}=k2\pi \left(k\in \mathbb{Z}\right)$$\iff x=\frac{\pi }{6}+k2\pi \left(k\in \mathbb{Z}\right)$ và giá trị nhỏ nhất của hàm số là – 1, đạt được khi $\cos \left(x-\frac{\pi }{6}\right)=-1$$\iff x-\frac{\pi }{6}=\pi +k2\pi \left(k\in \mathbb{Z}\right)$$\iff x=\frac{7\pi }{6}+k2\pi \left(k\in \mathbb{Z}\right)$.

c) Ta có y = sin⁴ x + cos⁴ x = (sin² x + cos² x)² – 2sin² x cos² x

= 1 – 2 (sin x cos x)² = $1-2.{\left(\frac{\sin 2x}{2}\right)}^2$= $1-\frac{1}{2}{\sin }^{2}2x$ 

= $1-\frac{1}{2}.\frac{1-\cos 4x}{2}$ = $1-\frac{1}{4}+\frac{1}{4}\cos 4x$ = $\frac{3}{4}+\frac{1}{4}\cos 4x$.

Vì – 1 ≤ cos 4x ≤ 1 nên $-\frac{1}{4}\le \frac{1}{4}\cos 4x\le \frac{1}{4}$, do đó $\frac{3}{4}-\frac{1}{4}\le \frac{3}{4}+\frac{1}{4}\cos 4x\le \frac{3}{4}+\frac{1}{4}$

hay $\frac{1}{2}\le \frac{3}{4}+\frac{1}{4}\cos 4x\le 1\forall x\in ℝ$.

Vậy giá trị lớn nhất của hàm số là 1, đạt được khi cos 4x = 1 ⇔ 4x = k2π (k ∈ ℤ)

$\iff x=k\frac{\pi }{2}\left(k\in \mathbb{Z}\right)$.

Giá trị nhỏ nhất của hàm số là $\frac{1}{2}$, đạt được khi cos 4x = – 1 ⇔ 4x = π + k2π (k ∈ ℤ)

$\iff x=\frac{\pi }{4}+k\frac{\pi }{2}\left(k\in \mathbb{Z}\right)$.

d) Ta có y = cos 2x + 2cos x − 1

= (2cos² x – 1) + 2cos x – 1

= 2cos² x + 2cos x – 2

= 2t² + 2t – 2 với t = cos x ∈ [– 1; 1].

Xét hàm số y = 2t² + 2t – 2 trên đoạn [– 1; 1]. Hàm số này có đồ thị như trong hình vẽ dưới đây.

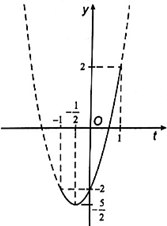
Từ đồ thị ở hình trên ta suy ra được giá trị lớn nhất của hàm số đã cho là 2, đạt được khi cos x = 1 ⇔ x = k2π (k ∈ ℤ) và giá trị nhỏ nhất của hàm số là $-\frac{5}{2}$, đạt được khi $\cos x=-\frac{1}{2}$$\iff x=\pm \frac{2\pi }{3}+k2\pi \left(k\in \mathbb{Z}\right)$.

Xem thêm các bài giải SBT Toán lớp 11 Kết nối tri thức hay, chi tiết khác:

Bài 3: Hàm số lượng giác

Bài 4: Phương trình lượng giác cơ bản

Bài tập cuối chương 1

Bài 5: Dãy số

Bài 6: Cấp số cộng

Bài 7: Cấp số nhân