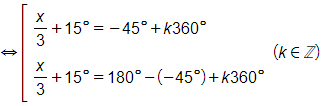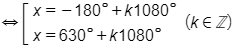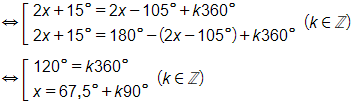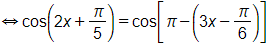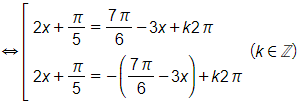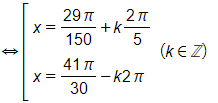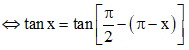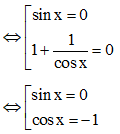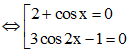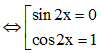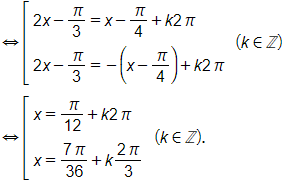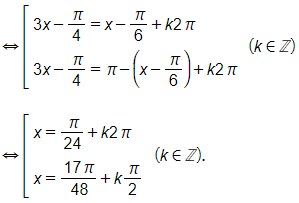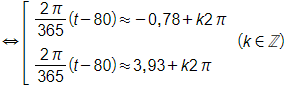Giải SBT Toán lớp 11 Bài 4: Phương trình lượng giác cơ bản
Bài 1.25 trang 24 SBT Toán 11 Tập 1: Giải các phương trình sau:
a) ;
b) ;
c) 3tan 2x + = 0;
d) cot (2x – 3) = cot 15°.
Lời giải:
a)
b)
.
c) 3tan 2x + = 0
.
d) cot (2x – 3) = cot 15°
⇔ 2x – 3 = 15° + k180° (k∈ ℤ)
⇔ 2x = 3 + 15° + k180° (k∈ ℤ)
⇔ x = 1,5 + 7,5° + k90° (k∈ ℤ).
Bài 1.26 trang 24 SBT Toán 11 Tập 1: Giải các phương trình sau:
a) sin(2x + 15°) + cos(2x – 15°) = 0;
b) ;
c) tan x + cot x = 0;
d) sin x + tan x = 0.
Lời giải:
a) Ta có sin(2x + 15°) + cos(2x – 15°) = 0
⇔ sin(2x + 15°) = – cos(2x – 15°)
⇔ sin(2x + 15°) = – sin[90° – (2x – 15°)]
⇔ sin(2x + 15°) = sin[– 90° + (2x – 15°)]
⇔ sin(2x + 15°) = sin(2x – 105°)
Không xảy ra trường hợp 120° = k360°.
Vậy phương trình đã cho có nghiệm x = 67,5° + k90° (k ∈ ℤ).
b)
c) Ta có tan x + cot x = 0
⇔ tan x = – cot x
⇔ tan x = cot(π – x)
. Vô lí.
Vậy phương trình đã cho vô nghiệm.
d) Điều kiện cos x ≠ 0 .
Ta có sin x + tan x = 0
⇔ sin x = 0 (do sin2 x + cos2 x = 1)
⇔ x = kπ (k ∈ ℤ).
Vì x = kπ (k ∈ ℤ) thoả mãn điều kiện cos x ≠ 0 nên nghiệm của phương trình đã cho là
x = kπ (k ∈ ℤ).
Bài 1.27 trang 24 SBT Toán 11 Tập 1: Giải các phương trình sau:
a) (2 + cos x)(3cos 2x – 1) = 0;
b) 2sin 2x – sin 4x = 0;
c) cos6 x – sin6 x = 0;
d) tan 2x cot x = 1.
Lời giải:
a) Ta có (2 + cos x)(3cos 2x – 1) = 0
+ Phương trình 2 + cos x = 0 vô nghiệm vì – 1 ≤ cos x ≤ 1.
+ Gọi α là góc thoả mãn cos α = . Ta có
3cos 2x – 1 = 0 ⇔ cos 2x = cos α ⇔ 2x = ± α + k2π (k ∈ ℤ) ⇔ x = + kπ (k ∈ ℤ).
Vậy nghiệm của phương trình đã cho là x = + kπ (k ∈ ℤ) với cos α = .
b) Ta có 2sin 2x – sin 4x = 0
⇔ 2sin 2x – 2sin 2x cos 2x = 0
⇔ 2sin 2x(1 – cos2x) = 0
Do sin2 2x + cos2 2x = 1 nên cos 2x = 1 kéo theo sin 2x = 0, do đó phương trình đã cho tương đương với
sin 2x = 0 ⇔ 2x = kπ (k ∈ ℤ) .
c) Ta có cos6 x – sin6 x = 0
⇔ cos6 x = sin6 x
⇔ (cos2 x)3 = (sin2 x)3
⇔ cos2 x = sin2 x
⇔ cos2 x – sin2 x = 0
⇔ cos 2x = 0
Từ đó ta được 2x = + kπ (k ∈ ℤ) hay .
d) Điều kiện sin x ≠ 0 và cos 2x ≠ 0.
Ta có tan 2x cot x = 1
⇔ tan 2x = tan x
⇔ 2x = x + kπ (k ∈ ℤ)
⇔ x = kπ (k ∈ ℤ).
Ta thấy x = kπ (k ∈ ℤ) không thoả mãn điều kiện sin x ≠ 0.
Vậy phương trình đã cho vô nghiệm.
a) và ;
b) và .
Lời giải:
a) Giá trị tương ứng của hai hàm số và bằng nhau nếu
b) Giá trị tương ứng của hai hàm số và bằng nhau nếu
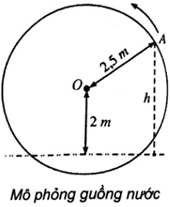
với x là thời gian quay của guồng (x ≥ 0), tính bằng phút; ta quy ước rằng y > 0 khi gầu ở trên mặt nước và y < 0 khi gầu ở dưới mặt nước.
a) Khi nào chiếc gầu ở vị trí cao nhất? Thấp nhất?
b) Chiếc gầu cách mặt nước 2 mét lần đầu tiên khi nào?
Lời giải:
a) Vì nên và do đó ta có
hay .
Suy ra, gầu ở vị trí cao nhất khi
. Do x ≥ 0 nên .
Vậy gầu ở vị trí cao nhất tại các thời điểm phút.
Tương tự, gầu ở vị trí thấp nhất khi
. Do x ≥ 0 nên .
Vậy gàu ở vị trí thấp nhất tại các thời điểm 0, 1, 2, 3, ... phút.
b) Gầu cách mặt nước 2 m khi
Do x ≥ 0 nên .
Vậy chiếc gầu cách mặt nước 2 m lần đầu tiên tại thời điểm phút.
với t ∈ ℤ và 0 < t ≤ 365.
a) Vào ngày nào trong năm thì thành phố A có ít giờ ánh sáng mặt trời nhất?
b) Vào ngày nào trong năm thì thành phố A có nhiều giờ ánh sáng mặt trời nhất?
c) Vào ngày nào trong năm thì thành phố A có khoảng 10 giờ ánh sáng mặt trời?
Lời giải:
Vì nên , do đó
hay .
a) Ngày thành phố A có ít giờ ánh sáng mặt trời nhất ứng với
Vì 0 < t ≤ 365 nên k = 1 suy ra t = + 365 = 353,75.
Như vậy, vào ngày thứ 353 của năm, tức là khoảng ngày 20 tháng 12 thì thành phố A sẽ có ít giờ ánh sáng mặt trời nhất.
b) Ngày thành phố A có nhiều giờ ánh sáng mặt trời nhất ứng với
Vì 0 < t ≤ 365 nên k = 0 suy ra t = = 171,25.
Như vậy, vào ngày thứ 171 của năm, tức là khoảng ngày 20 tháng 6 thì thành phố A sẽ có nhiều giờ ánh sáng mặt trời nhất.
c) Thành phố A có khoảng 10 giờ ánh sáng mặt trời trong ngày nếu
Từ đó ta được 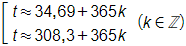
Vì 0 < t ≤ 365 nên k = 0 suy ra t ≈ 34,69 hoặc t ≈ 308,3.
Như vậy, vào khoảng ngày thứ 34 của năm, tức là ngày 3 tháng 2 và ngày thứ 308 của năm, tức là ngày 4 tháng 11 thành phố A sẽ có 10 giờ ánh sáng mặt trời.
Xem thêm các bài giải SBT Toán lớp 11 Kết nối tri thức hay, chi tiết khác: