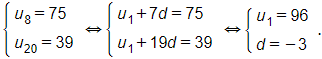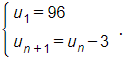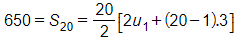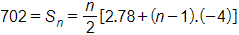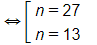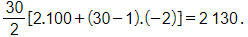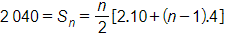Giải SBT Toán 11 (Kết nối tri thức) Bài 6: Cấp số cộng

Giải SBT Toán lớp 11 Bài 6: Cấp số cộng

Bài 2.11 trang 36 SBT Toán 11 Tập 1: Mỗi dãy số (u_n) sau có phải là một cấp số cộng hay không? Nếu có, hãy tìm số hạng đầu và công sai của nó:

a) u_n = 4 – 3n;

b) u_n = n² + 1;

c) u_n = 2n + 5;

d) u₁ = 3, u_{n + 1} = u_n + n.

Lời giải:

a) Từ u_n = 4 – 3n suy ra u_{n + 1} = 4 – 3(n + 1) = 4 – 3n – 3 = 1 – 3n.

Như vậy u_{n + 1} – u_n = (1 – 3n) – (4 – 3n) = – 3 không đổi với mọi n.  

Vậy dãy số đã cho là cấp số cộng với số hạng đầu u₁ = 4 – 3 = 1 và công sai d = – 3.

b) Từ u_n = n² + 1 suy ra u_{n + 1} = (n + 1)² + 1 = n² + 2n + 2.

Như vậy u_{n + 1} – u_n = (n² + 2n + 2) – (n² + 1) = 2n + 1, phụ thuộc vào n.

Vậy dãy số đã cho không là cấp số cộng.

c) Từ u_n = 2n + 5 suy ra u_{n + 1} = 2(n + 1) + 5 = 2n + 7.

Như vậy u_{n + 1} – u_n = (2n + 7) – (2n + 5) = 2 không đổi với mọi n.

Vậy dãy số đã cho là cấp số cộng với số hạng đầu u₁ = 2 + 5 = 7 và công sai d = 2.

d) Từ hệ thức truy hồi ta có u_{n + 1} = u_n + n, suy ra u_{n + 1} – u_n = n, phụ thuộc vào n.

Vậy dãy số đã cho không là cấp số cộng.

Bài 2.12 trang 36 SBT Toán 11 Tập 1: Số hạng thứ tám của một cấp số cộng là 75 và số hạng thứ hai mươi là 39.

a) Tìm số hạng đầu và công sai của cấp số cộng.

b) Tìm hệ thức truy hồi cho cấp số cộng.

c) Tìm công thức số hạng thứ n của cấp số cộng.

Lời giải:

a) Do số hạng thứ tám của một cấp số cộng là 75 và số hạng thứ hai mươi là 39 nên ta có

Vậy cấp số cộng có số hạng đầu u₁ = 96 và công sai d = – 3.

b) Ta có  u_{n + 1} = u_n + d = u_n – 3.

Vậy hệ thức truy hồi của cấp số cộng này là 

c) Công thức tổng quát của cấp số cộng này là

u_n = u₁ + (n – 1)d = 96 – (n – 1).3 = 99 – 3n.

Bài 2.13 trang 36 SBT Toán 11 Tập 1: Tổng 20 số hạng đầu của một cấp số cộng với công sai bằng 3 là 650. Tìm số hạng đầu của cấp số cộng này.

Lời giải:

Áp dụng công thức tính tổng n số hạng đầu của cấp số cộng với n = 20 và d = 3 ta có

⇔ 2u₁ + 57 = 65

⇔ u₁ = 4.

Vậy số hạng đầu của cấp số cộng đã cho là u₁ = 4.

Bài 2.14 trang 37 SBT Toán 11 Tập 1: Tìm x để 2x, 3x + 2 và 5x + 3 là các số hạng liên tiếp của một cấp số cộng.

Lời giải:

Vì 2x, 3x + 2, 5x + 3 là ba số hạng liên tiếp của một cấp số cộng nên ta suy ra

(3x + 2) – 2x = (5x + 3) – (3x + 2)

⇔ x + 2 = 2x + 1

⇔ x = 1.

Thử lại, ta có ba số tìm được là 2, 5, 8 thoả mãn bài toán.

Vậy x = 1.

Bài 2.15 trang 37 SBT Toán 11 Tập 1: Phải lấy tổng của bao nhiêu số hạng đầu của một cấp số cộng có số hạng đầu là 78 và công sai là – 4 để được tổng là 702?

Lời giải:

Áp dụng công thức tính tổng của n số hạng đầu của cấp số cộng ta có

⇔ n(160 – 4n) = 1 404

⇔ 160n – 4n² – 1 404 = 0

Suy ra n = 13 hoặc n = 27, tức là ta cần lấy 13 hoặc 27 số hạng đầu.

Bài 2.16 trang 37 SBT Toán 11 Tập 1: Một bức tường trang trí có dạng hình thang, rộng 2,4 m ở đáy và rộng 1,2 m ở đỉnh (hình vẽ bên). Các viên gạch hình vuông có kích thước 10 cm × 10 cm phải được đặt sao cho mỗi hàng ở phía trên chứa ít hơn một viên so với hàng ở ngay phía dưới nó. Hỏi sẽ cần bao nhiêu viên gạch hình vuông như vậy để ốp hết bức tường đó?

Lời giải:

Đổi 2,4 m = 240 cm; 1,2 m = 120 cm.

Số viên gạch ở hàng đầu tiên (ứng với đáy lớn) là u₁ = 240 : 10 = 24 (viên).

Số viên gạch ở hàng trên cùng (ứng với đáy nhỏ) là u_n = 120 : 10 = 12 (viên).

Vì mỗi hãng ở phía trên chứa ít hơn một viên so với hàng ở ngay phía dưới nó nên số viên gạch ở mỗi hàng (tính từ dưới lên) lập thành một cấp số cộng có công sai d = – 1 và số hạng đầu u₁ = 24.

Như vậy, u_n = u₁ + (n – 1)d = 24 + (n – 1) . (– 1) = 25 – n. Mà u_­n = 12 nên 25 – n = 12.

Suy ra n = 13. 

Vậy số viên gạch hình vuông cần thiết để ốp hết bức tường đó là

$S_{13}=\frac{\left(u_1+u_{13}\right).13}{2}=\frac{\left(12+24\right).13}{2}=234$ (viên gạch).

Bài 2.17 trang 37 SBT Toán 11 Tập 1: Một cầu thang bằng gạch có tổng cộng 30 bậc. Bậc dưới cùng cần 100 viên gạch. Mỗi bậc tiếp theo cần ít hơn hai viên gạch so với bậc ngay trước nó.

a) Cần bao nhiêu viên gạch cho bậc trên cùng?

b) Cần bao nhiêu viên gạch để xây cầu thang?

Lời giải:

Theo bài ra ta có số viên gạch ở mỗi bậc thang (tính từ dưới lên) lập thành một cấp số cộng gồm 30 số với số hạng đầu u₁ = 100 và công sai d = – 2.

Do đó, công thức của cấp số cộng biểu thị số viên gạch cho mỗi bậc cầu thang như sau:

u₁ = 100; u_{n + 1} = u­_n + (– 2) với n ≥ 1.

a) Bậc trên cùng là bậc thứ 30. Do đó, số viên gạch cần cho bậc trên cùng là

u₃₀ = u₁ + (30 – 1)d = 100 + 29 . (– 2) = 42 (viên gạch).

b) Ta có S₃₀ = u₁ + u₂ + ... + u₃₀ = 

Như vậy, ta cần 2 130 viên gạch để xây cầu thang.

Bài 2.18 trang 37 SBT Toán 11 Tập 1: Có bao nhiêu hàng ghế trong một góc khán đài của một sân vận động, biết rằng góc khán đài đó có 2 040 chỗ ngồi, hàng ghế đầu tiên có 10 chỗ ngồi và mỗi hàng ghế sau có thêm 4 chỗ ngồi so với hàng ghế ngay trước nó?

Lời giải:

Số ghế ở mỗi hàng của góc khán đài lập thành một cấp số cộng với số hạng đầu u₁ = 10 và công sai d = 4.

Áp dụng công thức tính tổng n số hạng đầu của cấp số cộng với S_n = 2 040, u₁ = 10, d = 4 để tìm n, ta có

⇔ n(16 + 4n) = 4 080

⇔ 4n² + 16n – 4 080 = 0

⇔ n = 30 hoặc n = – 34 (loại).

Suy ra n = 30, tức là góc khán đài đó có 30 hàng ghế.

Bài 2.19 trang 37 SBT Toán 11 Tập 1: Nếu anh Nam nhận được lời mời làm việc cho một công ty nước ngoài với mức lương khởi điểm là 35 000 đô la mỗi năm và được tăng thêm 1 400 đô la lương mỗi năm, thì sẽ mất bao nhiêu năm làm việc để tổng lương mà anh Nam nhận được là 319 200 đô la?

Lời giải:

Lương mỗi năm của anh Nam lập thành một cấp số cộng với số hạng đầu u₁ = 35 000 và công sai d = 1 400.

Áp dụng công thức tính tổng n số hạng đầu của cấp số cộng với S_n = 319 200, u₁ = 35 000, d = 1 400, ta có

319 200 = S_n = $\frac{n}{2}$[2 . 35 000 + (n – 1) .1 400]

⇔ n(68 600 + 1 400n) = 638 400

⇔ 1 400n² + 68 600n – 638 400 = 0

Suy ra n = 8 hoặc n = – 57 (loại). Do đó n = 8.

Vậy sau 8 năm làm việc thì tổng lương mà anh Nam nhận được là 319 200 đô la.

Bài 2.20 trang 37 SBT Toán 11 Tập 1: Nếu p, m và q lập thành một cấp số cộng thì dễ thấy $m=\frac{p+q}{2}$. Số m gọi là trung bình cộng của p và q. Cho hai số p và q, nếu ta tìm được k số khác m₁, m₂, ..., m_k sao cho p, m₁, m₂, …, m_k, q lập thành một cấp số cộng, chúng ta nói rằng chúng ta đã “chèn k trung bình cộng vào giữa p và q”.

a) Hãy chèn ba trung bình cộng vào giữa 4 và 12.

b) Tìm bốn trung bình cộng nằm giữa 16 và 91.

Lời giải:

a) Theo định nghĩa, chèn ba trung bình cộng vào giữa 4 và 12 ta được cấp số cộng có số hạng đầu u₁ = 4 và u_{2 + 3} = u₅ = 12.

Do tính chất của cấp số cộng nên u₅ = u₁ + (5 – 1)d = 4 + 4d. Suy ra d = 2.

Khi đó u₂ = 4 + 2 = 6, u₃ = 6 + 2 = 8, u₄ = 8 + 2 = 10.

Vậy chèn ba trung bình cộng vào giữa 4 và 12 ta được cấp số cộng là: 4, 6, 8, 10, 12.

b) Theo định nghĩa, chèn bốn trung bình cộng vào giữa 16 và 91 ta được cấp số cộng có số hạng đầu u₁ = 16 và u_{2 + 4} = u₆ = 91.

Do tính chất của cấp số cộng nên u₆ = u₁ + (16 – 1)d = 16 + 5d. Suy ra d = 15.

Khi đó u₂ = 16 + 15 = 31, u₃ = 31 + 15 = 46, u₄ = 46 + 15 = 61, u₅ = 61 + 15 = 76.

Vậy chèn bốn trung bình cộng vào giữa 16 và 91 ta được cấp số cộng là 16, 31, 46, 61, 76, 91.

Vậy bốn số cần tìm là 31, 46, 61, 76.

Xem thêm các bài giải SBT Toán lớp 11 Kết nối tri thức hay, chi tiết khác:

Bài tập cuối chương 1

Bài 5: Dãy số

Bài 7: Cấp số nhân

Bài tập cuối chương 2

Bài 8: Mẫu số liệu ghép nhóm