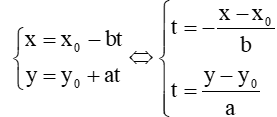Trong mặt phẳng Oxy, cho đường thẳng ∆ đi qua điểm M0(x0; y0) và nhận vectơ n (a; b) làm vectơ pháp tuyến. Với mỗi điểm M(x; y)
407
13/06/2023
Hoạt động khám phá 3 trang 48 Toán lớp 10 Tập 2: Trong mặt phẳng Oxy, cho đường thẳng ∆ đi qua điểm M0(x0; y0) và nhận →n(a; b) làm vectơ pháp tuyến. Với mỗi điểm M(x; y) thuộc ∆, chứng tỏ rằng điểm M(x; y) có tọa độ thỏa mãn phương trình:
a(x – x0) + b(y – y0) = 0 hay ax + by + c = 0 (với c = – ax0 – by0).
Trả lời
Vì đường thẳng ∆ nhận →n(a; b) làm vectơ pháp tuyến nên nhận →u(-b; a) làm vectơ chỉ phương. Khi đó phương trình tham số của đường thẳng ∆ là:
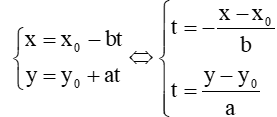
⇒ −x−x0b=y−y0a=t
⇔−x−x0b=y−y0a=t
⇔ -a(x – x0) = b(y – y0)
⇔ a(x – x0) + b(y – y0) = 0
⇔ ax + by – ax0 – by0 = 0 (*)
Đặt c = – ax0 – by0 thì (*) ⇔ ax + by + c = 0.
Xem thêm lời giải bài tập SGK Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Bài tập cuối chương 8
Bài 1: Toạ độ của vectơ
Bài 2: Đường thẳng trong mặt phẳng toạ độ
Bài 3: Đường tròn trong mặt phẳng toạ độ
Bài 4: Ba đường conic trong mặt phẳng tọa độ
Bài tập cuối chương 9