Chứng minh rằng tứ giác ABCD là một hình bình hành khi và chỉ khi vecto BC = AD

Bài 4.3 trang 50 Toán 10 Tập 1: Chứng minh rằng tứ giác ABCD là một hình bình hành khi và chỉ khi vecto BC = AD

Trả lời

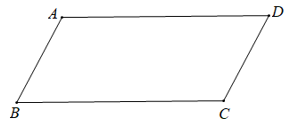
+ Giả sử tứ giác ABCD là hình bình hành

⇒ AD // BC (tính chất hình bình hành)

$\Rightarrow \overrightarrow{AD}$ và $\overrightarrow{BC}$ cùng phương

$\Rightarrow \overrightarrow{AD}$ và $\overrightarrow{BC}$ cùng hướng.

Mà AD = BC (tính chất hình bình hành)

$\Rightarrow \overrightarrow{AD}=\overrightarrow{BC}$ 

+ Giả sử tứ giác ABCD có $\overrightarrow{BC}=\overrightarrow{AD}$ suy ra $\overrightarrow{BC}$và $\overrightarrow{AD}$ cùng phương, cùng hướng và cùng độ dài.

Þ BC = AD (1) và AD, BC song song hoặc trùng nhau.

Nếu hai đường thẳng AD, BC trùng nhau thì bốn điểm A, B, C, D cùng nằm trên một đường thẳng, điều này không xảy ra vì ABCD là tứ giác. Vậy AD // BC. (2)

Từ (1) và (2) suy ra tứ giác ABCD là hình bình hành (dấu hiệu nhận biết).

Vậy tứ giác ABCD là một hình bình hành khi và chỉ khi $\overrightarrow{BC}=\overrightarrow{AD}$.

Xem thêm lời giải bài tập SGK Toán lớp 10 Kết nối tri thức hay, chi tiết khác:

Bài 6: Hệ thức lượng trong tam giác

Bài tập cuối chương 3

Bài 7: Các khái niệm mở đầu

Bài 8: Tổng và hiệu của hai vectơ

Bài 9: Tích của một vecto với một số

Bài 10: Vectơ trong mặt phẳng tọa độ