Bài 4.4 trang 50 Toán 10 Tập 1: Cho hình vuông ABCD có hai đường chéo cắt nhau tại O. Hãy chỉ ra tập S gồm tất cả các vectơ khác , có điểm đầu và điểm cuối thuộc tập hợp {A; B; C; D; O}. Hãy chia tập S thành các nhóm sao cho hai vectơ thuộc cùng một nhóm khi và chỉ khi chúng bằng nhau.
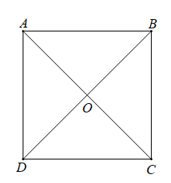
Các vectơ khác →0, có điểm đầu và điểm cuối thuộc tập hợp {A; B; C; D; O} là:
→AB,→AC,→AD,→AO,→BA,→BC,→BD,→BO,→CA,→CB,→CD,→CO,→DA,→DB,→DC,→DO,→OA,→OC,→OB,→OD.
Khi đó: S = {→AB;→AC; →AD;→AO;→BA;→BC;→BD;→BO;→CA;→CB;→CD;→CO;→DA;→DB;→DC;→DO;→OA;→OC;→OB;→OD}.
Hai vectơ bằng nhau trong tập hợp S là:
→AB=→DC;→BA=→CD;→AD=→BC;→DA=→CB;→OA=→CO;→OB=→DO; →OC=→AO;→OD=→BO.
Khi đó tập S được chia thành các nhóm là:
Nhóm 1: {→AB;→DC};
Nhóm 2: {→AD;→BC};
Nhóm 3: {→BA;→CD};
Nhóm 4: {→DA;→CB};
Nhóm 5: {→OA;→CO};
Nhóm 6: {→OB;→DO};
Nhóm 7: {→OC;→AO};
Nhóm 8: {→OD;→BO}.
Xem thêm lời giải bài tập SGK Toán lớp 10 Kết nối tri thức hay, chi tiết khác:
Bài 6: Hệ thức lượng trong tam giác
Bài 8: Tổng và hiệu của hai vectơ