Cho tam giác ABC có góc B nhọn, AD và CE là hai đường cao

Bài 9 trang 73 Toán lớp 10 Tập 1: Cho tam giác ABC có góc B nhọn, AD và CE là hai đường cao.

a) Chứng minh $\frac{S_{BDE}}{S_{BAC}}=\frac{BD.BE}{BA.BC}$

b) Biết rằng S_ABC = 9S_BDE và DE = $2\sqrt{2}$. Tính cosB và bán kính đường tròn ngoại tiếp tam giác ABC.

Trả lời

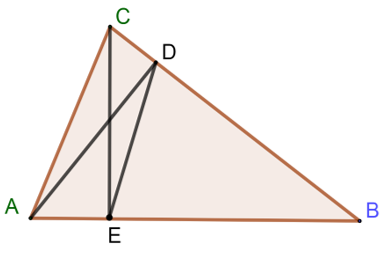
a) Ta có: $\frac{S_{BDE}}{S_{BAC}}=\frac{\frac{1}{2}.BE.BD.\sin B}{\frac{1}{2}.BA.BC.\sin B}=\frac{BE.BD}{BA.BC}$

b) Theo đề ta có: $\frac{S_{BDE}}{S_{ABC}}=\frac{BD.BE}{BA.BC}=\frac{BD}{BA}.\frac{BE}{BC}=\frac{1}{9}$ (1)

Xét tam giác BCE vuông tại E ta có: $\cos B=\frac{BE}{BC}$ (2)

Xét tam giác BDA vuông tại D ta có: $\cos B=\frac{BD}{BA}$ (3)

Thay (2) và (3) vào (1) ta được :${\cos }^{2}B=\frac{1}{9}\Rightarrow \cos B=\frac{1}{3}$ ( Vì góc B nhọn)

Mặt khác, ${\sin }^{2}B+{\cos }^{2}B=1\Rightarrow {\sin }^{2}B=1-\frac{1}{9}=\frac{8}{9}\Rightarrow \sin B=\frac{2\sqrt{2}}{3}$

Áp dụng định lí sin cho tam giác BED ta có:$R^{\text{'}}=\frac{ED}{2\sin B}=\frac{3}{2}$

Xét tam giác BED và BCA ta có:

Góc B chung

$\frac{BE}{BC}=\frac{1}{3}$và $\frac{BD}{BA}=\frac{1}{3}$

Vậy tam giác AED đồng dạng với tam giác BCA nên $\frac{ED}{CA}=\frac{1}{3}$

Theo đề ta có:

$\frac{S_{BDE}}{S_{ABC}}=\frac{\frac{BD.BE.DE}{4R\text{'}}}{\frac{BA.BC.AC}{4R}}=\frac{BD}{BA}.\frac{BE}{BC}.\frac{DE}{AC}.\frac{R}{R^{\text{'}}}=\frac{1}{27}.\frac{R}{R^{\text{'}}}=\frac{1}{9}$

$\Rightarrow R=3R^{\text{'}}=3.\frac{3}{2}=\frac{9}{2}$