Cho tam giác ABC có AB = 6, AC = 8 và góc A = 60độ. a) Tính diện tích tam giác ABC

Bài 6 trang 73 Toán lớp 10 Tập 1: Cho tam giác ABC có AB = 6, AC = 8 và $\widehat{A}={60}^o$.

a) Tính diện tích tam giác ABC.

b) Gọi I là tâm đường tròn ngoại tiếp tam giác ABC. Tính diện tích tam giác IBC.

Trả lời

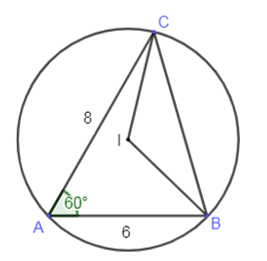
a) $S_{ABC}=\frac{1}{2}AB.AC.\sin A=\frac{1}{2}\mathrm{6.8.}\sin {60}^0=12\sqrt{3}$

b)
Áp dụng định lí côsin ta có:

$\begin{array}{l}B{C}^2=A{B}^2+A{C}^2-2AB.AC.\cos A=8^2+6^2-\mathrm{2.8.6.}\cos {60}^0=52\\ \Rightarrow BC=\sqrt{52}\end{array}$

Ta có: $R=IB=IC=\frac{BC}{2\sin A}=\frac{\sqrt{52}}{2\sin {60}^0}=\frac{2\sqrt{39}}{3}$(áp dụng định lí sin)

Mặt khác, ta có: $\widehat{CAB}$ và $\widehat{CIB}$ cùng chắn cung BC

Mà $\widehat{CAB}$ là góc nội tiếp và  $\widehat{CIB}$ góc ở tâm

Nên $\widehat{CIB}=2\widehat{CAB}={2.60}^0={120}^0$

Vậy $S_{IBC}=\frac{1}{2}.IB.IC.\sin \widehat{CIB}=\frac{1}{2}.{\left(\frac{2\sqrt{39}}{3}\right)}^2.\sin {120}^0=\frac{13\sqrt{3}}{3}$