Giải SGK Toán 10 (Chân trời sáng tạo): Bài tập cuối chương 3

Giải Toán 10: Bài tập cuối chương 3

Bài tập

Bài 1 trang 59 Toán lớp 10 Tập 1: Tìm tập xác định của các hàm số sau:

a) y = 4x² – 1;

b) $y=\frac{1}{x^2+1};$

c) $y=2+\frac{1}{x}.$

Lời giải:

a)

Hàm số y = 4x² – 1 là hàm số bậc hai, do đó nó có tập xác định là $D=ℝ$.

b)          

Ta có: x² ≥ 0 với mọi số thực x

⇒ x² + 1 > 0 với mọi số thực x

⇒ x² + 1 ≠ 0 với mọi số thực x

Do đó, hàm số $y=\frac{1}{x^2+1}$ có tập xác định là $D=ℝ$.

c)

Điều kiện xác định của hàm số là x ≠ 0.

Do đó, hàm số $y=2+\frac{1}{x}$ có tập xác định là $D=ℝ\backslash \text{{}0\}$.

Bài 2 trang 59 Toán lớp 10 Tập 1: Tìm điều kiện của m để mỗi hàm số sau đây là một hàm số bậc hai:

a) y = (1 – 3m)x² + 3;

b) y = (4m – 1)(x – 7)²;

c) y = 2(x² + 1) + 11 – m.

Lời giải:

a) Hàm số y = (1 – 3m)x² + 3 là hàm số bậc hai khi và chỉ khi

1 – 3m ≠ 0

⇔ 3m ≠ 1

$\iff m\ne \frac{1}{3}$ 

Vậy $m\ne \frac{1}{3}$ thì hàm số đã cho là hàm số bậc hai.

b) Có:

y = (4m – 1)(x – 7)² = (4m – 1)(x² – 14x + 49) = (4m – 1)x² – 14(4m – 1)x + 49(4m – 1)

Hàm số này là hàm số bậc hai khi và chỉ khi

4m – 1 ≠ 0

⇔ 4m ≠ 1

$\iff m\ne \frac{1}{4}$ 

Vậy $m\ne \frac{1}{4}$ thì hàm số đã cho là hàm số bậc hai.

c) Có:

y = 2(x² + 1) + 11 – m = 2x² + 2 + 11 – m = 2x² + 13 – m

Hàm số này luôn là hàm số bậc hai với mọi giá trị của m.

Bài 3 trang 59 Toán lớp 10 Tập 1: Vẽ đồ thị các hàm số sau:

a) y = x² – 4x + 3;

b) y = - x² – 4x + 5;

c) y = x² – 4x + 5;

d) y = -x² – 2x – 1.

Lời giải:

a) Xét hàm số y = x² – 4x + 3, ta có:

Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = f(x) = x² – 4x + 3 là một parabol (P):

– Có đỉnh S với hoành độ x_S = 2, tung độ y_S­ = –1;

– Có trục đối xứng là đường thẳng x = 2 (đường thẳng này đi qua đỉnh S và song song với trục Oy);

– Bề lõm quay lên trên vì a > 0;

– Cắt trục tung tại điểm có tung độ bằng 3, tức là đồ thị đi qua điểm có tọa độ (0; 3);

– Ngoài ra, phương trình x² – 4x + 3 = 0 có hai nghiệm phân biệt là x₁ = 1, x₂ = 3. Do đó, đồ thị còn đi qua hai điểm (1; 0), (3; 0).

Ta vẽ được đồ thị như hình dưới:

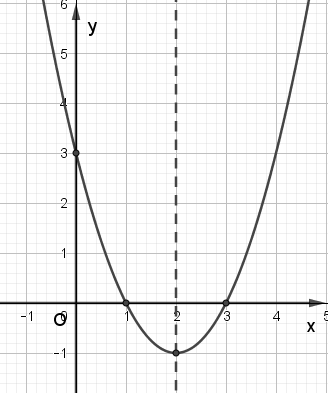
b) Xét hàm số y = –x² – 4x + 5, ta có:

Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = f(x) = –x² – 4x + 5 là một parabol (P):

– Có đỉnh S với hoành độ x_S = –2, tung độ y_S­ = 9;

– Có trục đối xứng là đường thẳng x = –2 (đường thẳng này đi qua đỉnh S và song song với trục Oy);

– Bề lõm quay xuống dưới vì a < 0;

– Cắt trục tung tại điểm có tung độ bằng 5, tức là đồ thị đi qua điểm có tọa độ (0; 5);

– Ngoài ra, phương trình –x² – 4x + 5 = 0 có hai nghiệm phân biệt là x₁ = –5, x₂ = 1. Do đó, đồ thị còn đi qua hai điểm (–5; 0), (1; 0).

Ta vẽ được đồ thị như hình dưới:

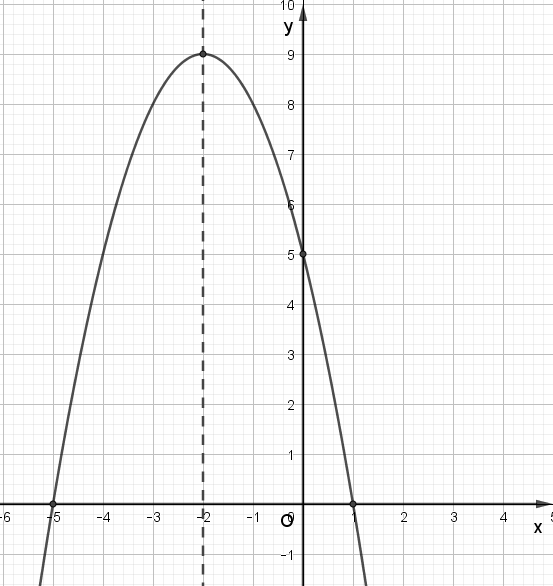
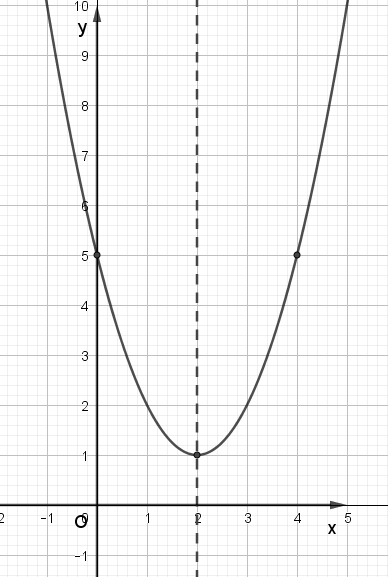
c) Xét hàm số y = x² – 4x + 5, ta có:

Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = f(x) = x² – 4x + 5 là một parabol (P):

– Có đỉnh S với hoành độ x_S = 2, tung độ y_S­ = 1;

– Có trục đối xứng là đường thẳng x = 1 (đường thẳng này đi qua đỉnh S và song song với trục Oy);

– Bề lõm quay lên trên vì a > 0;

– Cắt trục tung tại điểm có tung độ bằng 5, tức là đồ thị đi qua điểm có tọa độ (0; 5);

– Ngoài ra, đồ thị hàm số y = x² – 4x + 5 còn đi qua điểm (4; 5).

Ta vẽ được đồ thị như hình dưới:

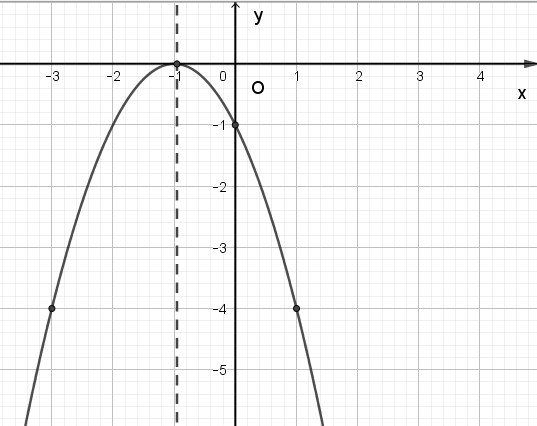
d) Xét hàm số y = –x² – 2x – 1, ta có:

Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = f(x) = –x² – 2x – 1 là một parabol (P):

– Có đỉnh S với hoành độ x_S = –1, tung độ y_S­ = 0;

– Có trục đối xứng là đường thẳng x = –1 (đường thẳng này đi qua đỉnh S và song song với trục Oy);

– Bề lõm quay xuống dưới vì a < 0;

– Cắt trục tung tại điểm có tung độ bằng –1, tức là đồ thị đi qua điểm có tọa độ (0; –1);

– Ngoài ra, đồ thị hàm số y = –x² – 2x – 1 còn đi qua hai điểm (–3; –4) và (1; –4).

Ta vẽ được đồ thị như hình dưới:

Bài 4 trang 59 Toán lớp 10 Tập 1: Một vận động viên chạy xe đạp trong 1 giờ 30 phút đầu với vận tốc trung bình là 42km/h. Sau đó người này nghỉ tại chỗ 15 phút và tiếp tục đạp xe 2 giờ liền với vận tốc 30km/h.

a) Hãy biểu thị quãng đường s (tính bằng ki lô mét) mà người này đi được sau t phút bằng một hàm số.

b) Vẽ đồ thị biểu diễn hàm số s theo t.

Lời giải:

Đổi: 42 km/h = 0,7 km/phút, 30 km/h = 0,5 km/phút

a) Trong 1 giờ 30 phút = 90 phút đầu với vận tốc trung bình là 42 km/h nên ta có:

Với 0  ≤  t  ≤ 90 thì s = f(t) = 0,7t

Sau đó, người này nghỉ tại chỗ 15 phút nên ta có:

Với 90 < t ≤ 105 thì s = f(t) = 0,7 . 90 = 63

Người đó tiếp tục đạp xe 2 giờ = 120 phút liền với vận tốc 30 km/h nên ta có:

Với 105 < t ≤ 225 thì s = f(t) = 63 + 0,5 . (t – 105) = 63 + 0,5t – 52,5 = 10,5 + 0,5t.

Vậy ta có hàm số như sau: $f\left(t\right)=\left\{\begin{array}{l}0,7t\left(0\le t\le 90\right)\\ 63(90<t\le 105)\\ 10,5+0,5t(105<t\le 225)\end{array}\right.$ .

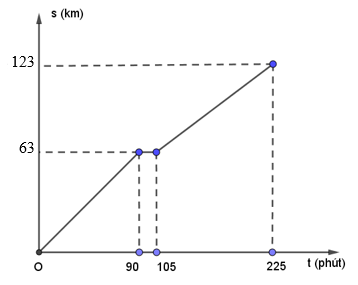
b) Trong đoạn [0; 90], đồ thị hàm số là đường thẳng đi qua điểm (0; 0) và (90; 63).

Trong khoảng (90; 105], đồ thị hàm số là đường thẳng s = 63, song song với trục Ot.

Trong khoảng (105; 120], đồ thị hàm số là đường thẳng đi qua điểm (225; 123).

Ta có đồ thị như hình vẽ:

Bài 5 trang 59 Toán lớp 10 Tập 1: Biết rằng hàm số y = 2x² + mx + n giảm trên khoảng (-∞; 1), tăng trên khoảng (1; + ∞) và có tập giá trị là [9; +∞). Xác định giá trị của m và n.

Lời giải:

Xét hàm số y = 2x² + mx + n là hàm số bậc hai.

Do hàm số y = 2x² + mx + n giảm trên khoảng (–∞; 1), tăng trên khoảng (1; +∞) và có tập giá trị là [9; +∞) nên ta có bảng biến thiên:

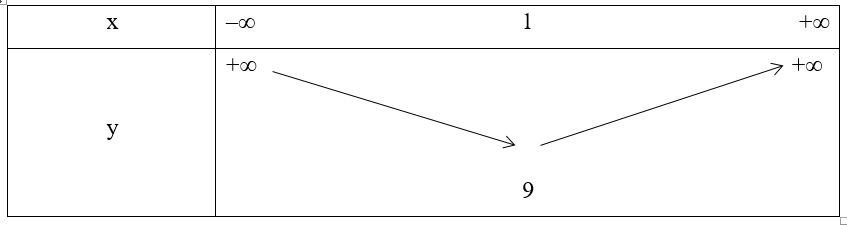
Trong đó, ta có đỉnh của Parabol là (1; 9)

$\Rightarrow \frac{-m}{2.2}=1\iff$–m = 4 $\iff$ m = –4.

Lại có: 2.1² – 4.1 + n = 9 ⇔ 2 – 4 + n = 9 ⇔ n = 11.

Vậy m = –4, n = 11.

Bài 6 trang 59 Toán lớp 10 Tập 1: Nhảy bungee là một trò chơi mạo hiểm. Trong trò chơi này, người chơi đứng ở vị trí trên cao, thắt dây an toàn và nhảy xuống. Sợi dây này có tính đàn hồi và được tính toán chiều dài để nó kéo người chơi lại khi gần chạm đất (hoặc mặt nước). Chiếc cầu trong Hình 1 có bộ phận chống đỡ dạng parabol. Một người thực hiện một cú nhảy bungee từ giữa cầu xuống với dây an toàn. Người này cần trang bị sợi dây an toàn dài bao nhiêu mét? Biết rằng chiều dài của sợi dây đó bằng một phần ba khoảng cách từ vị trí bắt đầu nhảy đến mặt nước.

Lời giải:

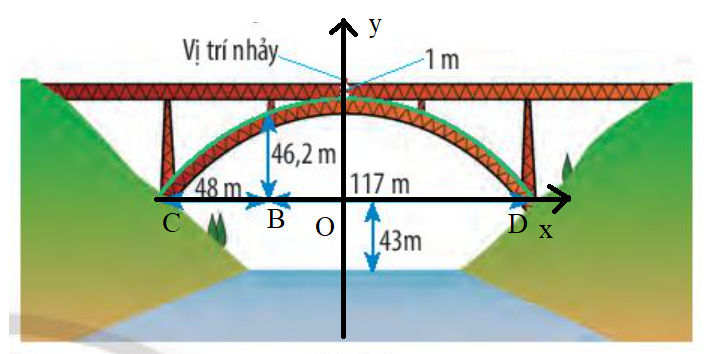
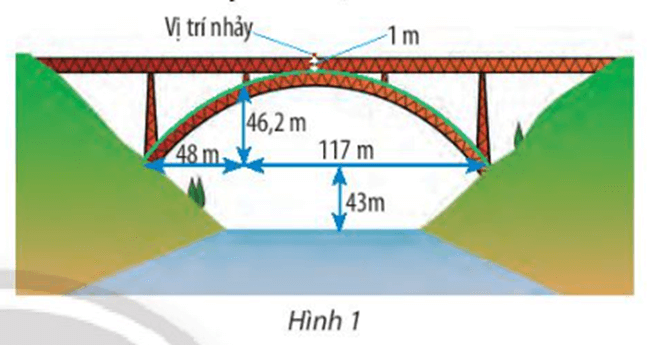
Đặt hệ trục tọa độ Oxy như hình vẽ, gọi phương trình của parabol có dạng: y = ax² + bx + c  (a, b, c là các số thực, a ≠ 0).

Ta có: OB = CD : 2 – CB = (48 + 117) : 2 – 48 = 34,5 (m)

OC = CD : 2 = (48 + 117) : 2 = 82,5 (m)

Từ đó ta có điểm thuộc parabol là (34,5; 46,2)

⇒ a.34,5² + b.34,5 + c = 46,2

⇒ 1190,25a + 34,5b + c = 46,2                                                     (1)

Ngoài ra, parabol còn cắt trục hoành tại hai điểm (–82,5; 0) và (82,5; 0) nên ta có:

a.(–82,5)² + b.(–82,5) + c = 0 ⇒ 6806,25a – 82,5b + c = 0 (2)

a.82,5² + b.82,5 + c = 0 ⇒ 6806,25a + 82,5b + c = 0 (3)

Từ (1), (2), (3) ta có hệ phương trình: $\left\{\begin{array}{l}1190,25a+34,5b+c=46,2\\ 6806,25a-82,5b+c=0\\ 6806,25a+82,5b+c=0\end{array}\right.\iff \left\{\begin{array}{l}a=-\frac{77}{9360}\\ b=0\\ c=\frac{46585}{832}\end{array}\right.$

Xét đỉnh parabol có hoành độ x = 0 và tung độ y = $\frac{46585}{832}$.

Khoảng cách từ vị trí nhảy đến mặt nước là: 1 + $\frac{46585}{832}$ + 43 = $\frac{83193}{832}$ (m)

Vậy độ dài dây an toàn cần thiết là: $\frac{83193}{832}$: 3 ≈ 33,33 m.

Bài 7 trang 59 Toán lớp 10 Tập 1: Giả sử một máy bay cứu trợ đang bay theo phương ngang và bắt đầu thả hàng từ độ cao 80m, lúc đó máy bay đang bay với vận tốc 50m/s. Để thùng hàng hỗ trợ rơi trúng vị trí được chọn, máy bay cần thả hàng ở vị trí nào? Biết rằng nếu chọn gốc tọa độ là hình chiếu trên mặt đất của vị trí hàng cứu trợ bắt đầu được thả, thì tọa độ của hàng cứu trợ được cho bởi hệ sau:

$\left\{\begin{array}{l}x=v_{0}t\\ y=h-\frac{1}{2}g{t}^2\end{array}\right.$

Trong đó, v₀ là vận tốc ban đầu và h là độ cao tính từ khi hàng rời máy bay.

Lưu ý: Chuyển động này được xem là chuyển động ném ngang.

Lời giải:

Theo đề bài, ta có biểu thức tọa độ của thùng hàng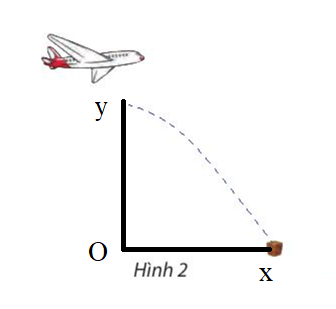: $\left\{\begin{array}{l}x=50t\\ y=80-\frac{1}{2}g{t}^2\end{array}\right.$.

Đặt hệ trục tọa độ như hình vẽ. Khi thùng hàng rơi đúng vị trí, ta có:

y = 0 $\iff 80-\frac{1}{2}g{t}^2=0\iff \frac{1}{2}g{t}^2=80\iff g{t}^2=160\iff t^2=\frac{160}{g}\iff t=\frac{\sqrt{160}}{g}$ (do t là thời gian nên t > 0).

Lấy g ≈ 10 m/s².

Khi đó, ta có: $x=50.\sqrt{\frac{160}{10}}\approx 200$ (m)

Vậy để thùng hàng cứu trợ rơi đúng vị trí được chọn, máy bay cần bắt đầu thả hàng từ vị trí cách vị trí được chọn khoảng 200 m.

Xem thêm lời giải bài tập SGK Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Bài 1: Hàm số và đồ thị

Bài 2: Hàm số bậc hai

Bài 1: Giá trị lượng giác của một góc từ 0 độ đến 180 độ

Bài 2: Định lí côsin và định lí sin

Bài 3: Giải tam giác và ứng dụng thực tế