a) Cho tam giác ABC không phải là tam giác vuông với góc A nhọn và góc C >= góc B

Hoạt động khám phá 1 trang 66 Toán lớp 10 tập 1:

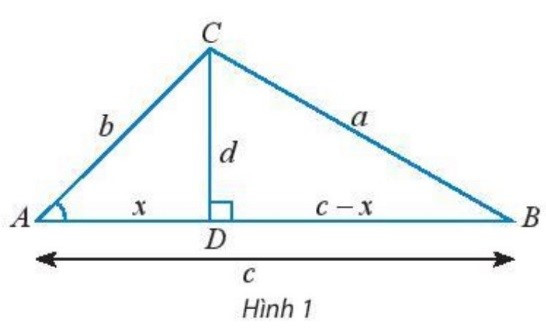
a) Cho tam giác ABC không phải là tam giác vuông với góc A nhọn và $\widehat{C}\ge \widehat{B}$.Vẽ đường cao CD và đặt tên các độ dài như trong hình 1. Hãy thay dấu $\boxed{?}$ bằng chữ cái thích hợp để chứng minh công thức $a^2=b^2+c^2-2bc\cos A$ theo gợi ý sau:

Xét tam giác vuông BCD , ta có: $a^2=d^2+{(c-x)}^2=d^2+c^2+x^2-2cx$ (1)

Xét tam giác vuông ACD, ta có:   $b^2=d^2+x^2\Rightarrow d^2=b^2-x^2$                (2)

                                                     $\cos A=\frac{\boxed{?}}{b}\Rightarrow \boxed{?}=b\cos A$                  (3)          

Thay (2) và (3) vào (1), ta có : $a^2=b^2+c^2-2bc\cos A$

b) Cho tam giác ABC với góc A tù. Làm tương tự như trên chứng minh rằng ta cũng có:

$a^2=b^2+c^2-2bc\cos A$

c) Cho tam giác ABC vuông tại A.Hãy chứng tỏ công thức $a^2=b^2+c^2-2bc\cos A$ có thể viết là $a^2=b^2+c^2$

Trả lời

a) Xét tam giác vuông BCD , ta có: $a^2=d^2+{(c-x)}^2=d^2+c^2+x^2-2cx$ (1)

Xét tam giác vuông ACD, ta có:   $b^2=d^2+x^2\Rightarrow d^2=b^2-x^2$                    (2)

                                                     $\cos A=\frac{x}{b}\Rightarrow x=b\cos A$                       (3)          

Thay (2) và (3) vào (1), ta có : $a^2=b^2+c^2-2bc\cos A$

b)

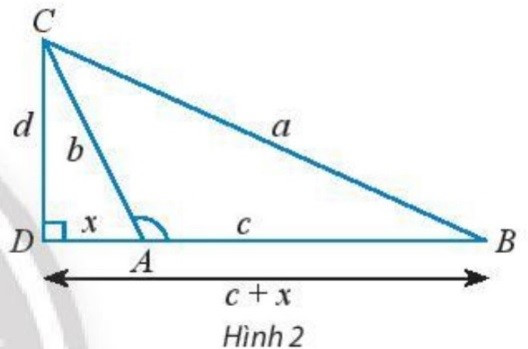
Xét tam giác vuông BCD , ta có: $a^2=d^2+{(c+x)}^2=d^2+c^2+x^2+2cx$     (1)

Xét tam giác vuông ACD, ta có:   $b^2=d^2+x^2\Rightarrow d^2=b^2-x^2$                    (2)

                      Vì A là góc tù nên  $\cos A=\frac{-x}{b}\Rightarrow x=-b\cos A$                      (3)          

Thay (2) và (3) vào (1), ta có : $a^2=b^2+c^2-2bc\cos A$         

c)

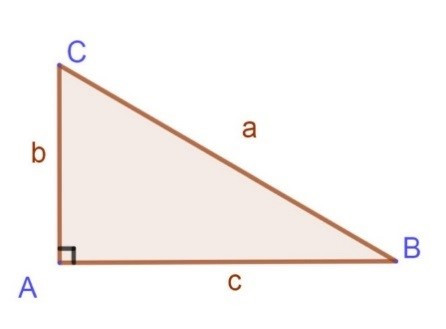
Theo đề ta có : $a^2=b^2+c^2-2bc\cos A$

Mà $\cos A=\cos {90}^0=0$

Nên $a^2=b^2+c^2-2bc.0=c^2+b^2$

Xem thêm lời giải bài tập SGK Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Bài tập cuối chương 3

Bài 1: Giá trị lượng giác của một góc từ 0 độ đến 180 độ

Bài 2: Định lí côsin và định lí sin

Bài 3: Giải tam giác và ứng dụng thực tế

Bài tập cuối chương 4

Bài 1: Khái niệm vectơ