Dạng 2: Xác định loại tam giác dựa vào số đo góc của tam giác đó có đáp án
-
188 lượt thi
-
10 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Cho tam giác ABC như hình vẽ:
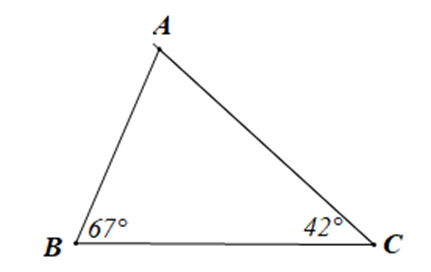
Tính số đo góc A và cho biết tam giác ABC là tam gác gì?
Xem đáp án
Đáp án đúng là: A
Xét tam giác ABC có ˆA+ˆB+ˆC=180∘ (định lí tổng ba góc trong một tam giác)
Suy ra ˆA=180∘−ˆB−ˆC
Hay ˆA=180∘−67∘−42∘=71∘
Ta thấy 42° < 67° < 71° < 90° nên góc A, góc B, góc C đều là góc nhọn.
Vậy ˆA=71∘ và tam giác ABC là tam giác nhọn.
Câu 2:
Cho tam giác ABC như hình vẽ có ^ADC=60∘.
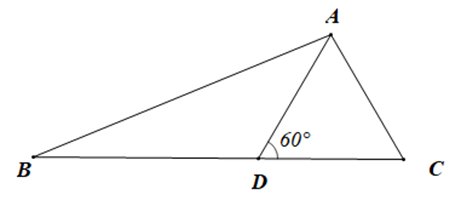
Tam giác ABD là tam giác gì?
Xem đáp án
Đáp án đúng là: D
Ta có ^ADB và ^ADC là hai góc kề bù nên ^ADB+^ADC=180∘ (tính chất hai góc kề bù)
Suy ra ^ADB=180∘−^ADC
Hay ^ADB=180∘−60∘=120∘>90∘
Do đó góc ADB là góc tù
Vậy tam giác ABD là tam giác tù.
Câu 3:
Cho hình vẽ:
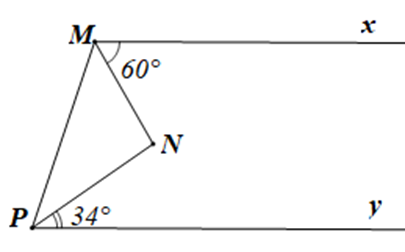
Biết Mx // Py, ^xMN=60∘ và ^NPy=34∘. Tính số đo góc MNP và tam giác MNP là tam giác gì?
Xem đáp án
Đáp án đúng là: D
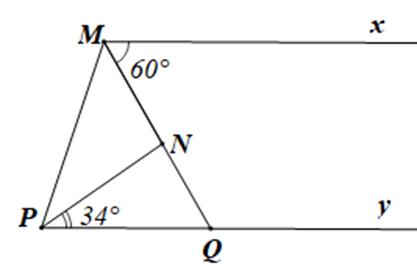
Kéo dài MN cắt Py tại Q.
Vì Mx // Py nên ta có: ^xMQ=^MQP (hai góc so le trong)
Mà ^xMQ=60∘ do đó ^MQP=60∘
Xét tam giác NPQ có ^MNP là góc ngoài của tam giác tại đỉnh N
Nên ^MNP=^NPQ+^NQP (tính chất góc ngoài của tam giác)
Suy ra ^MNP=34∘+60∘=94∘>90∘
Do đó góc MNP là góc tù
Vậy ^MNP=94∘ và tam giác MNP là tam giác tù.
Câu 4:
Cho hình vẽ biết ^ABC=50∘,^ACB=40∘ và ^BAE=^AED.
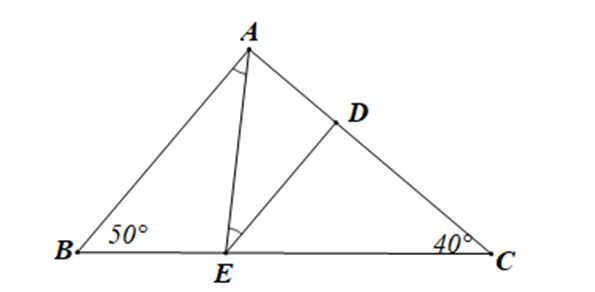
Tam giác CDE là tam giác gì?
Xem đáp án
Đáp án đúng là: C
Xét tam giác ABC có ˆA+ˆB+ˆC=180∘ (định lí tổng ba góc trong một tam giác)
Suy ra ˆA=180∘−ˆB−ˆC
Hay ˆA=180∘−50∘−40∘=90∘
Xét hai đường thẳng DE và AB có: ^BAE=^AED
Mà hai góc này ở vị trí so le trong
Do đó DE // AB
Suy ra ^EDC=ˆA (hai góc ở vị trí đồng vị)
Mà ˆA=90∘
Do đó ^EDC=90∘
Vậy tam giác CDE là tam giác vuông.
Câu 5:
Cho hình vẽ dưới đây.
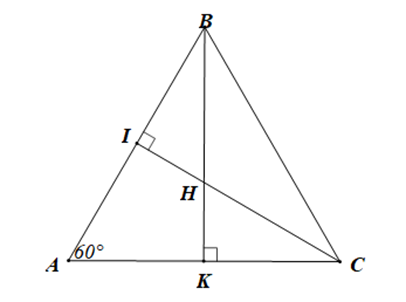
Tam giác BHC là tam giác gì?
Xem đáp án
Đáp án đúng là: A
Tam giác AIC vuông tại I (ˆI=90∘) nên ˆA+^ACI=90∘ (trong tam giác vuông, hai góc nhọn phụ nhau)
Suy ra ˆA=90∘−^ACI (1)
Tam giác CHK vuông tại K (ˆK=90∘) nên ^CHK+^KCH=90∘ (trong tam giác vuông, hai góc nhọn phụ nhau)
Suy ra ^CHK=90∘−^KCH (2)
Mà ^ACI chính là góc ^KCH (3)
Từ (1), (2) và (3) ta có: ^CHK=ˆA=60∘
Lại có ^CHK và ^BHC là hai góc kề bù nên ^CHK+^BHC=180∘ (tính chất hai góc kề bù)
Suy ra ^BHC=180∘−^CHK
Do đó ^BHC=180∘−60∘=120∘>90∘
Khi đó góc BHC là góc tù
Vậy tam giác BHC là tam giác tù.
Câu 6:
Cho tam giác ABC có ˆB=35∘,ˆC=65∘. Tia phân giác góc A cắt cạnh BC tại D.
Tam giác ADC là tam giác gì?
Xem đáp án
Đáp án đúng là: C
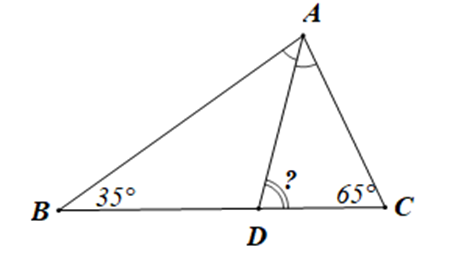
Xét tam giác ABC có ˆA+ˆB+ˆC=180∘ (định lí tổng ba góc trong một tam giác)
Suy ra ˆA=180∘−ˆB−ˆC
Hay ˆA=180∘−35∘−65∘=80∘
Mà tia AD là tia phân giác của ^BAC nên ^BAD=^CAD=12^BAC
Suy ra ^BAD=^CAD=12.80∘=40∘
Mặt khác: ^ADC là góc ngoài của tam giác ABD tại đỉnh D nên ^ADC=^BAD+ˆB
Hay ^ADC=40∘+35∘=75∘
Tam giác ADC có ^CAD=40∘<90∘,^ACD=65∘<90∘,^ADC=75∘<90∘
Do đó tam giác ADC có ba góc nhọn.
Vậy tam giác ADC là tam giác nhọn.
Câu 7:
Cho hình vẽ:
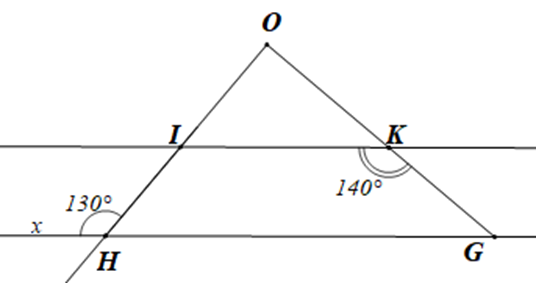
Biết IK // HG. Tam giác OIK là tam giác gì?
Xem đáp án
Đáp án đúng là: C
Vì IK // HG nên ^KIH=^OHx (hai góc so le trong)
Mà ^OHx=130∘ nên ^KIH=130∘
Lại có ^KIH và ^OIK là hai góc kề bù nên ^OIK+^KIH=180∘ (tính chất hai góc kề bù)
Suy ra ^OIK=180∘−^KIH
Do đó ^OIK=180∘−130∘=50∘
Xét tam giác OIK có ^IKG là góc ngoài của tam giác tại đỉnh K
Nên ^IKG=^OIK+^IOK (tính chất góc ngoài của tam giác)
Suy ra ^IOK=^IKG−^OIK
Hay ^IOK=140∘−50∘=90∘
Do đó góc IOK là góc vuông
Vậy tam giác OIK là tam giác vuông tại O.
Câu 8:
Cho hình vẽ như sau:
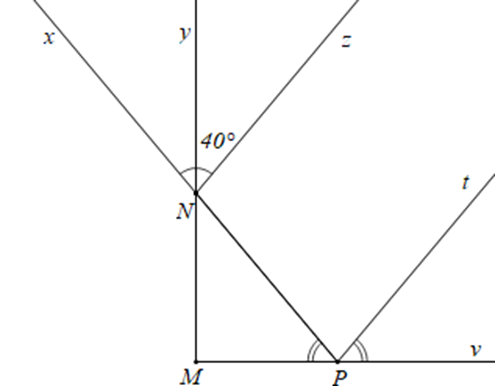
Biết tia Ny là tia phân giác của ^xNz,^yNz=40∘,^NPM=^tPv và Nz // Pt. Số đo của ^NPM là bao nhiêu và tam giác MNP là tam giác gì?
Xem đáp án
Đáp án đúng là: D
Vì tia Ny là tia phân giác của ^xNz nên ^yNz=12.^xNz (tính chất tia phân giác của một góc)
Suy ra ^xNz=2.^yNz
Mà ^yNz=40∘ nên ^xNz=2.^yNz=2.40∘=80∘
Lại có Nz // Pt nên ^xNz=^NPt (hai góc so le trong)
Do đó ^NPt=80∘
Ta lại có ^MPN+^NPt+^tPv=180∘
Mà ^NPM=^tPv, ^NPt=80∘
Suy ra ^NPM+80∘+^NPM=180∘
Hay 2.^NPM=180∘−80∘=100∘
Do đó ^NPM=100∘:2=50∘
Mặt khác ^MNP=^xNy (hai góc đối đỉnh) nên ^MNP=40∘
Xét tam giác MNP có ^NPM=50∘ và ^MNP=40∘ ta có:
^NMP+^MNP+^NPM=180∘ (định lí tổng ba góc trong một tam giác)
Suy ra ^NMP=180∘−^MNP−^NPM hay ^NMP=180∘−40∘−50∘=90∘
Suy ra tam giác MNP vuông tại M.
Vậy ta chọn phương án D.
Câu 9:
Cho tam giác ABC vuông tại A. Lấy điểm K nằm trên cạnh AC. Lấy điểm E nằm trên cạnh BK. Tam giác BEC là tam giác gì?
Xem đáp án
Đáp án đúng là: A
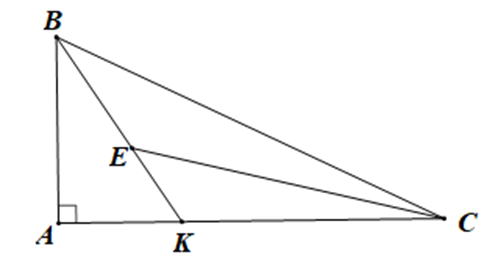
Tam giác ABC vuông tại A nên ˆA=90∘
Xét tam giác ABK vuông tại A (ˆA=90∘) có ^BKC là góc ngoài của tam giác tại đỉnh K
Do đó ^BKC=ˆA+^ABK (tính chất góc ngoài của tam giác)
Tương tự ta có ^BEC là góc ngoài của tam giác CKE tại đỉnh E nên ^BEC=^EKC+^ECK
Suy ra ^BEC=(ˆA+^ABK)+^ECK=ˆA+^ABK+^ECK
Do đó ^BEC>ˆA mà ˆA=90∘
Do đó ^BEC>90∘ là góc tù
Vậy tam giác BEC là tam giác tù.
Câu 10:
Cho hình vẽ:
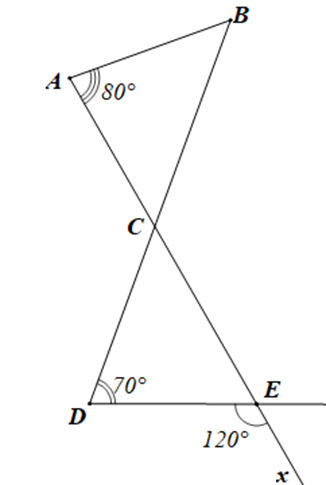
Tam giác ABC là tam giác gì?
Xem đáp án
Đáp án đúng là: B
Xét tam giác CDE có ^DEx là góc ngoài của tam giác tại đỉnh E
Nên ^DEx=ˆD+^DCE (tính chất góc ngoài của tam giác)
Suy ra ^DCE=^DEx−ˆD
Hay ^DCE=120∘−70∘=50∘
Lại có ^ACB=^DCE (hai góc đối đỉnh)
Nên ^ACB=50∘
Xét tam giác ABC có ˆA+ˆB+^ACB=180∘ (định lí tổng ba góc trong một tam giác)
Suy ra ˆB=180∘−ˆA−^ACB
Hay ˆB=180∘−80∘−50∘=50∘
Tam giác ABC có ˆA=80∘<90∘,ˆB=50∘<90∘,^ACB=50∘<90∘
Do đó ba góc của tam giác ABC đều là góc nhọn
Vậy tam giác ABC là tam giác nhọn.