Dạng 1: Tính số đo góc trong tam giác dựa vào định lí tổng ba góc trong một tam giác và góc ngoài của một tam giác có đáp án
-
186 lượt thi
-
10 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Cho tam giác ABC có ˆA=96° Số đo góc C là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
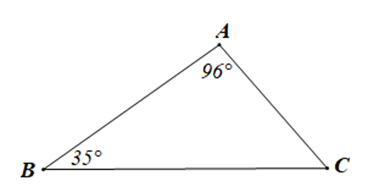
Xét tam giác ABC có (định lí tổng ba góc trong một tam giác)
Suy ra
Mà
Do đó
Vậy số đo góc C là 49°.
Câu 2:
Cho một chiếc thang dựa vào tường. Biết độ nghiêng của chiếc thang đó so với mặt đất là 68°, khi đó độ nghiêng của chiếc thang đó so với bức tường là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Ta vẽ tam giác ABC vuông tại A có \widehat B = 68^\circ để mô tả hình ảnh chiếc thang dựa vào tường như đề bài.
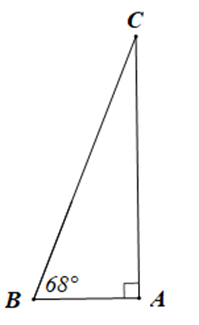
Trong tam giác ABC vuông tại A ta có: \widehat B + \widehat C = 90^\circ (trong tam giác vuông, hai góc nhọn phụ nhau)
Suy ra \widehat C = 90^\circ - \widehat B = 90^\circ - 68^\circ = 22^\circ
Vậy độ nghiêng của chiếc thang so với bức tường là 22°.
Câu 3:
Cho hình vẽ sau:
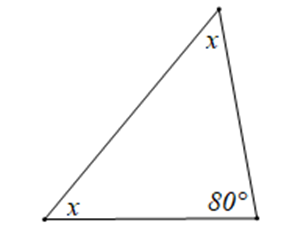
Số đo x là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Xét tam giác có trong hình vẽ, ta có: x + x + 80° = 180° (tổng ba góc trong một tam giác)
Suy ra 2x = 180° ‒ 80°
Hay 2x = 100°
Do đó x = 100° : 2 = 50°
Vậy x = 50°.
Câu 4:
Cho tam giác ABC có ba cạnh bằng nhau. Số đo góc A là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
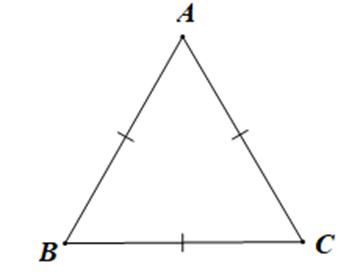
Tam giác ABC có ba cạnh bằng nhau nên là tam giác đều.
Do đó \widehat A = \widehat B = \widehat C
Mà \widehat A + \widehat B + \widehat C = 180^\circ (định lí tổng ba góc trong một tam giác)
Suy ra \widehat A + \widehat A + \widehat A = 180^\circ
Hay 3\widehat {.A} = 180^\circ
Do đó \widehat A = 180^\circ :3 = 60^\circ
Vậy số đo góc A bằng 60°.
Câu 5:
Cho tam giác ABC có \widehat A = 88^\circ ,\widehat B - \widehat C = 36^\circ . Số đo góc B và C lần lượt là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
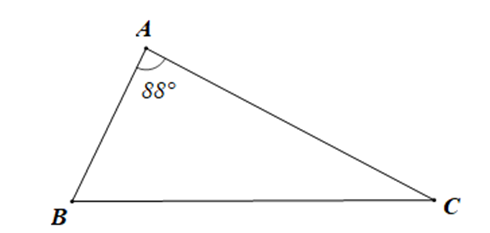
Xét tam giác ABC có (định lí tổng ba góc trong m\widehat B + \widehat C = 180^\circ - \widehat Aột tam giác)
Suy ra
Hay \widehat B + \widehat C = 180^\circ - 88^\circ = 92^\circ
Mặt khác \widehat B - \widehat C = 36^\circ
Suy ra \widehat B = \frac{{92^\circ + 36^\circ }}{2} = 64^\circ ,\widehat C = 92^\circ - \widehat B = 92^\circ - 64^\circ = 28^\circ
Vậy số đo góc B và C lần lượt là 64° và 28°.
Câu 6:
Cho tam giác ABC có \widehat B = 35^\circ ,\widehat C = 65^\circ . Tia phân giác góc A cắt cạnh BC tại D. Số đo góc ADC là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
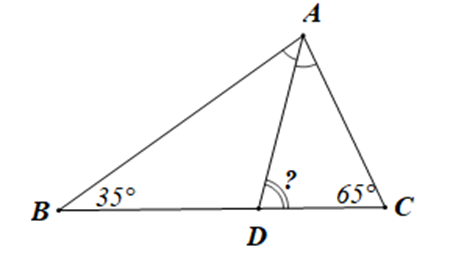
Xét tam giác ABC có \widehat A + \widehat B + \widehat C = 180^\circ (định lí tổng ba góc trong một tam giác)
Suy ra
Hay \widehat A = 180^\circ - 35^\circ - 65^\circ = 80^\circ
Mà tia AD là tia phân giác của \widehat {BAC}
Nên \widehat {BAD} = \widehat {CAD} = \frac{1}{2}\widehat {BAC} (tính chất tia phân giác của một góc)
Suy ra \widehat {BAD} = \widehat {CAD} = \frac{1}{2}.80^\circ = 40^\circ
Mặt khác: \widehat {ADC} là góc ngoài của tam giác ABD tại đỉnh D
Nên \widehat {ADC} = \widehat {BAD} + \widehat B (tính chất góc ngoài của một tam giác)
Hay \widehat {ADC} = 40^\circ + 35^\circ = 75^\circ
Vậy số đo góc ADC là 75°.
Câu 7:
Cho tam giác MNP có \widehat M = 70^\circ ,3\widehat N = 2\widehat P. Số đo góc N là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Xét tam giác MNP có \widehat M + \widehat N + \widehat P = 180^\circ (định lí tổng ba góc trong một tam giác)
Suy ra \widehat N + \widehat P = 180^\circ - 70^\circ = 110^\circ
Suy ra 2\left( {\widehat N + \widehat P} \right) = 2.110^\circ hay 2\widehat N + 2\widehat P = 220^\circ
Mà 3\widehat N = 2\widehat P
Nên 2\widehat N + 3\widehat N = 220^\circ
Hay 5\widehat N = 220^\circ
\widehat N = 220^\circ :5 = 44^\circ .
Vậy số đo góc N là 44°.
Câu 8:
Cho hình vẽ:
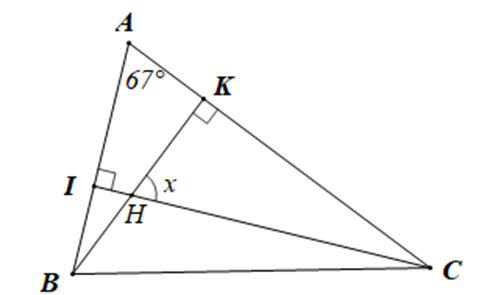
Số đo x là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Tam giác AIC vuông tại I \left( {\widehat I = 90^\circ } \right) nên \widehat A + \widehat {ACI} = 90^\circ (trong tam giác vuông, hai góc nhọn phụ nhau)
Suy ra \widehat A = 90^\circ - \widehat {ACI} (1)
Tam giác CHK vuông tại K \left( {\widehat K = 90^\circ } \right) nên \widehat {CHK} + \widehat {KCH} = 90^\circ (trong tam giác vuông, hai góc nhọn phụ nhau)
Suy ra \widehat {CHK} = 90^\circ - \widehat {KCH} (2)
Mà \widehat {ACI} chính là góc \widehat {KCH} (3)
Từ (1), (2) và (3) ta có: \widehat {CHK} = \widehat A = 67^\circ
Hay x = 67°.
Câu 9:
Để mỗi khi mưa, nước mưa có thể thoát xuống kịp thì người ta thường lợp mái ngói có độ dốc hai bên đều tạo với phương nằm ngang một góc bằng nhau có số đo từ 25° đến 35°.

Một nhà thiết kế nhà đã thiết kế hai bên mái nhà tạo với nhau một góc 120°. Hỏi độ dốc của mái nhà là bao nhiêu và mái nhà được thiết kế như vậy đã thỏa mãn độ dốc để nước mưa kịp thoát chưa?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta vẽ tam giác ABC có \widehat A = 120^\circ ,\widehat B = \widehat C như hình vẽ để mô tả mái nhà mà nhà thiết kế đã vẽ.
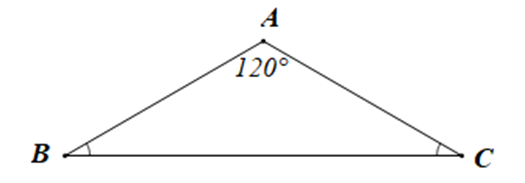
Xét tam giác ABC có \widehat A + \widehat B + \widehat C = 180^\circ (định lí tổng ba góc trong một tam giác)
Suy ra \widehat B + \widehat C = 180^\circ - \widehat A
Mà \widehat A = 120^\circ ,\widehat B = \widehat C nên \widehat B + \widehat B = 180^\circ - 120^\circ
Hay 2\widehat B = 60^\circ
Suy ra \widehat B = 30^\circ
Ta có: 25° < 30° < 35°
Do đó độ dốc của mái nhà là 30° và thỏa mãn yêu cầu về độ dốc.
Câu 10:
Cho hình vẽ như sau:
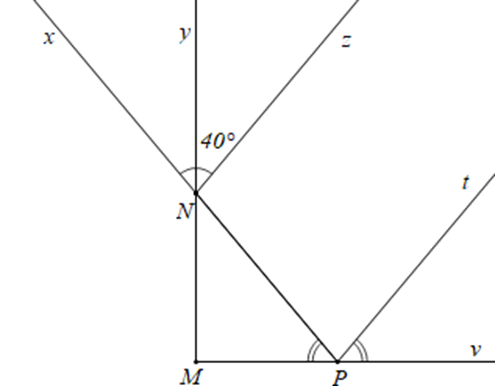
Biết tia Ny là tia phân giác của \widehat {xNz},\widehat {yNz} = 40^\circ ,\widehat {NPM} = \widehat {tPv} và Nz // Pt. Số đo của \widehat {NPM} là bao nhiêu và tam giác MNP là tam giác gì?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Vì tia Ny là tia phân giác của \widehat {xNz} nên \widehat {yNz} = \frac{1}{2}.\widehat {xNz} (tính chất tia phân giác của một góc)
Suy ra \widehat {xNz} = 2.\widehat {yNz}
Mà \widehat {yNz} = 40^\circ nên \widehat {xNz} = 2.\widehat {yNz} = 2.40^\circ = 80^\circ
Lại có Nz // Pt nên \widehat {xNz} = \widehat {NPt} (hai góc so le trong)
Do đó \widehat {NPt} = 80^\circ
Ta lại có \widehat {MPN} + \widehat {NPt} + \widehat {tPv} = 180^\circ
Mà \widehat {NPM} = \widehat {tPv}, \widehat {NPt} = 80^\circ
Suy ra \widehat {NPM} + 80^\circ + \widehat {NPM} = 180^\circ
Hay 2.\widehat {NPM} = 180^\circ - 80^\circ = 100^\circ
Do đó \widehat {NPM} = 100^\circ :2 = 50^\circ
Mặt khác \widehat {MNP} = \widehat {xNy} (hai góc đối đỉnh) nên \widehat {MNP} = 40^\circ
Xét tam giác MNP có \widehat {NPM} = 50^\circ và \widehat {MNP} = 40^\circ ta có:
\widehat {NMP} + \widehat {MNP} + \widehat {NPM} = 180^\circ (định lí tổng ba góc trong một tam giác)
Suy ra \widehat {NMP} = 180^\circ - \widehat {MNP} - \widehat {NPM} hay \widehat {NMP} = 180^\circ - 40^\circ - 50^\circ = 90^\circ
Suy ra tam giác MNP vuông tại M.
Vậy ta chọn phương án D.
