Trắc nghiệm Toán 7 KNTT Bài 14. Trường hợp bằng nhau thứ hai và thứ ba của tam giác có đáp án
Dạng 1: Tìm và chứng minh hai tam giác bằng nhau theo trường hợp cạnh - góc - cạnh từ đó chứng minh tính chất khác có đáp án
-
181 lượt thi
-
10 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Cho tam giác ABC và tam giác DEG có: AB = DE, ^ABC=^DEG. Điều kiện để DABC = DDEG theo trường hợp cạnh – góc – cạnh là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
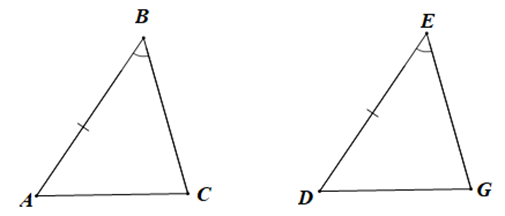
Vì DABC = DDEG theo trường hợp cạnh – góc – cạnh nên điều kiện về cặp góc bằng nhau của hai tam giác là góc xen kẽ giữa hai cạnh.
Mà ^ABC là góc xen kẽ giữa hai cạnh BA và BC, ^DEG là góc xen kẽ giữa hai cạnh ED và EG.
Lại có BA = ED
Do đó điều kiện còn lại là điều kiện về cạnh, đó là BC = EG.
Ta chọn phương án B.
Câu 2:
Cho hình vẽ sau:
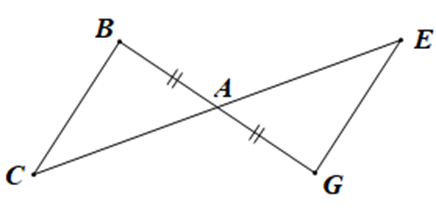
Điều kiện để DABC = DAGE theo trường hợp cạnh – góc – cạnh là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Vì DABC = DAGE theo trường hợp cạnh – góc – cạnh nên điều kiện về cặp góc bằng nhau của hai tam giác là góc xen kẽ giữa hai cạnh.
Mà ^BAC=^GAE (hai góc đối đỉnh)
Góc BAC xen kẽ giữa hai cạnh AB và AC, góc GAE xen kẽ giữa hai cạnh AG và AE.
Mà AB = AG nên điều kiện còn thiếu trong trường hợp này là điều kiện về cạnh, đó là AC = AE.
Vậy ta chọn phương án C.
Câu 3:
Cho hình vẽ dưới đây:
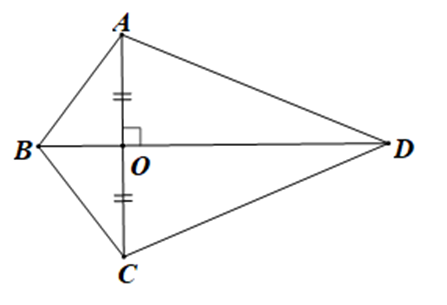
Số cặp tam giác bằng nhau theo trường hợp cạnh – góc – cạnh là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
+ Xét tam giác ABO và tam giác CBO có:
AO = CO, ^AOB=^COB(=90∘), BO là cạnh chung
Do đó DABO = DCBO (c.g.c)
+ Xét DAOD và DCOD có:
AO = CO, ^AOD=^COD(=90∘), OD là cạnh chung
Do đó D AOD = DCOD (c.g.c)
+ Vì DABO = DCBO (chứng minh trên)
Nên (hai góc tương ứng) và AB = CB (hai cạnh tương ứng)
Xét DABD và DCBD có:
AB = CB (chứng minh trên);
^ABD=^CBD (do ^ABO=^CBO)
BD là cạnh chung
Do đó DABD = DCBD (c.g.c)
Vậy có 3 cặp tam giác bằng nhau theo trường hợp cạnh – góc – cạnh.
Câu 4:
Cho tam giác BAC và tam giác MNP có BA = MN, ˆA=ˆM, CA = MP. Phát biểu nào sau đây là đúng:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
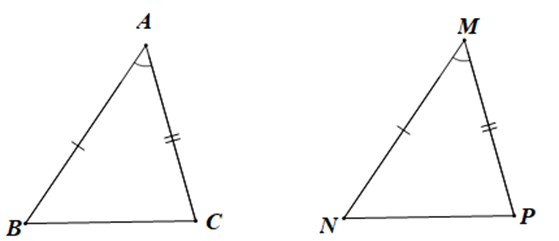
Xét DBAC và DMNP có:
BA = MN (giả thiết),
ˆA=ˆM (giả thiết),
CA = MP (giả thiết)
Do đó DBAC = DNMP (c.g.c)
Vậy ta chọn phương án A.
Câu 5:
Cho hình vẽ dưới đây:
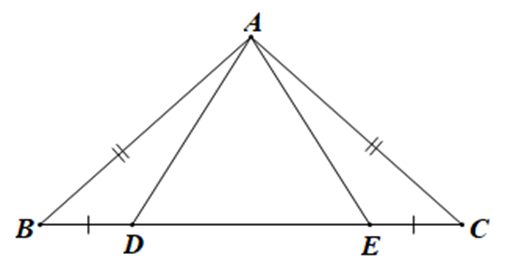
Biết AB = AC, BD = EC, ^ABC=^ACB. Xét các khẳng định sau:
(1) DABD = DACE;
(2) DABE = DACD.
Chọn câu đúng:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
+ Xét DABD và DACE có:
AB = AC (giả thiết),
^ABD=^ACE (giả thiết),
BD = CE (giả thiết)
Do đó DABD = DACE (c.g.c)
+ Vì BE = BD + DE, CD = CE + ED
Mà BD = CE (giả thiết) nên BE = CD.
Xét DABE và DACD có:
AB = AC (giả thiết),
^ABE=^ACD (giả thiết),
BE = CD (chứng minh trên)
Do đó DABE = DACD (c.g.c)
Vậy cả phương án A và B đều đúng, ta chọn phương án C.
Câu 6:
Cho DABC và DMNP có AB = NP, ˆB=ˆN=55∘, BC = NM. Biết ˆA=50∘, số đo góc P là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
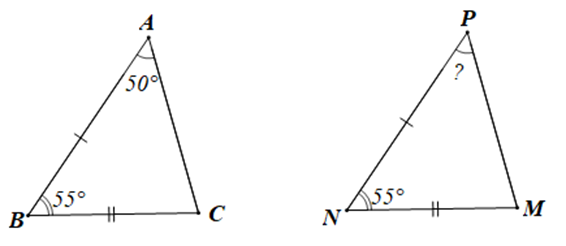
Xét DABC và DMNP có:
AB = NP (giả thiết),
ˆB=ˆN(=55∘) (giả thiết),
BC = NM (giả thiết),
Do đó DABC = DPNM (c.g.c)
Suy ra ˆA=ˆP=50∘ (hai góc tương ứng)
Vậy ˆP=50∘.
Câu 7:
Cho góc xOy khác góc bẹt, gọi Ot là tia phân giác của góc xOy. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA = OB. Trên tia đối của tia Ot lấy điểm C tuỳ ý. Chọn phát biểu đúng:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
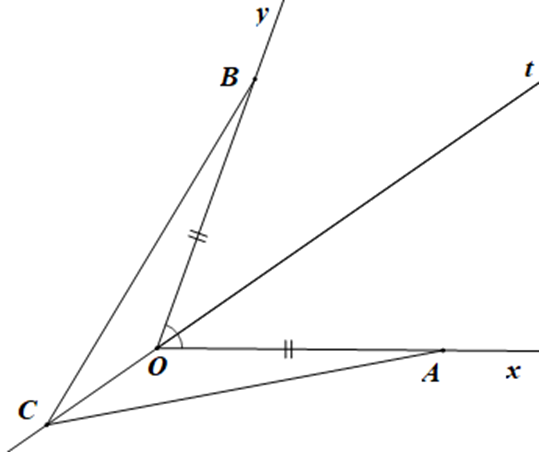
Vì tia Ot là tia phân giác của góc xOy nên ^xOt=^yOt (tính chất tia phân giác của một góc)
Mà ^xOt+^xOC=180∘ (tính chất hai góc kề bù) và ^yOt+^yOC=180∘ (tính chất hai góc kề bù)
Do đó ^xOC=^yOC hay ^AOC=^BOC
Xét tam giác AOC và tam giác BOC có:
OA = OB (giả thiết),
^AOC=^BOC (chứng minh trên),
OC là cạnh chung
Do đó DOAC = DOBC (c.g.c)
Suy ra CA = CB (hai cạnh tương ứng) và ^OCA=^OCB (hai góc tương ứng)
Nên tia CO là tia phân giác của ^ACB.
Vậy ta chọn phương án D.
Câu 8:
Cho tam giác ABC có AB = AC = BC, phân giác BD và CE cắt nhau tại O. Chọn phát biểu sai:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
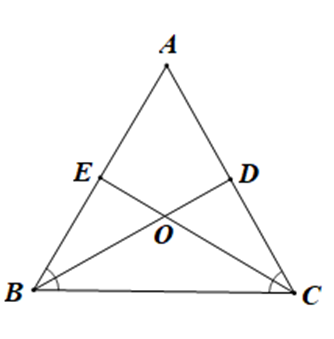
Tam giác ABC có AB = AC = BC (giả thiết) nên là tam giác đều
Do đó ˆA=^ABC=^ACB
CE là tia phân giác của ^ACB (giả thiết)
Nên ^ACE=^ECB=12^ACB (tính chất tia phân giác) (1)
Xét tam giác ACE và tam giác BCE có:
AC = BC (giả thiết),
^ACE=^ECB (chứng minh trên),
CE là cạnh chung
Do đó DACE = DBCE (c.g.c)
Suy ra ^AEC=^BEC (hai góc tương ứng)
Mà ^AEC+^BEC=180∘ (tính chất hai góc kề bù)
Nên ^AEC=^BEC=180∘2=90∘
Do đó CE ^ AB. Nên A là khẳng định đúng.
Mà BD là tia phân giác của ^ABC (giả thiết)
Nên ^ABD=^DBC=12^ABC (tính chất tia phân giác) (2)
Xét tam giác ABD và tam giác CBD có:
AB = BC (giả thiết),
^ABD=^DBC (chứng minh trên),
BD là cạnh chung
Do đó DABD = DCBD (c.g.c)
Suy ra ^ADB=^CDB (hai góc tương ứng)
Mà ^ADB+^CDB=180∘ (tính chất hai góc kề bù)
Nên ^ADB=^CDB=180∘2=90∘
Do đó BD ^ AC. Nên B là khẳng định sai và C là khẳng định đúng.
Từ (1) và (2) suy ra ^ABD=^DBC=^ACE=^ECB. Nên D là khẳng định đúng.
Vậy ta chọn phương án B.
Câu 9:
Cho góc nhọn xOy và một điểm A nằm trong góc đó. Kẻ AH ^ Ox tại H và AK ^ Oy tại K. Kéo dài AH một đoạn HB = AH và kéo dài AK một đoạn KC = AK. Nối OA, OB, OC. Chọn phát biểu đúng:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
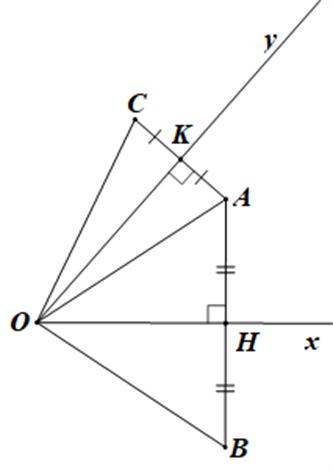
Xét tam giác OAH và tam giác OBH có:
OH là cạnh chung,
^OHA=^OHB(=90∘),
AH = BH (giả thiết)
Do đó DOAH = DOBH (c.g.c)
Suy ra OA = OB (hai cạnh tương ứng) (1)
Chứng minh tương tự ta cũng có DOKA = DOKC (c.g.c)
Suy ra OA = OC (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra OA = OB = OC. Do đó A là khẳng định đúng.
Vì DOAH = DOBH (c.g.c) (chứng minh trên)
Nên ^AOH=^BOH (hai góc tương ứng)
Suy ra OH là tia phân giác của ^AOB
Do đó ^AOH=^BOH=12^AOB (3)
Tương tự ta cũng có OK là tia phân giác của ^COA
Do đó ^KOA=^COK=12^COA (4)
Từ (3) và (4) ta có: ^KOA+^AOH=12^COA+12^AOB
Hay ^HOK=12(^COA+^AOB)=12^COB. Do đó B là khẳng định đúng
Vậy ta chọn phương án C.
Câu 10:
Cho hình vuông ABCD, trên cạnh AB lấy điểm M, trên cạnh BC lấy điểm N và trên cạnh DC lấy điểm P sao cho AM = BN = CP. Số đo góc MNP là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
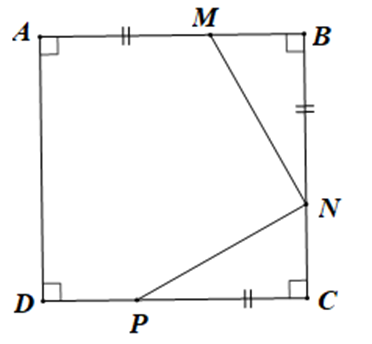
Vì ABCD là hình vuông (giả thiết) nên AB = BC (tính chất hình vuông)
Do đó AM + MB = BN + NC
Mà AM = BN (giả thiết) nên MB = NC.
Xét tam giác MBN và tam giác NCP có:
BN = CP (giả thiết),
ˆB=ˆC (=90∘, tính chất hình vuông),
MB = NC (chứng minh trên)
Do đó DMBN = DNCP (c.g.c)
Suy ra ^BMN=^CNP (hai góc tương ứng)
Mà ^BMN+^BNM=90∘ (trong tam giác BMN vuông tại B, hai góc nhọn phụ nhau)
Do đó ^BNM+^CNP=90∘
Mặt khác ^BNM+^MNP+^CNP=180∘
Suy ra ^MNP=180∘−(^BNM+^CNP)=180∘−90∘=90∘
Vậy ^MNP=90∘.
