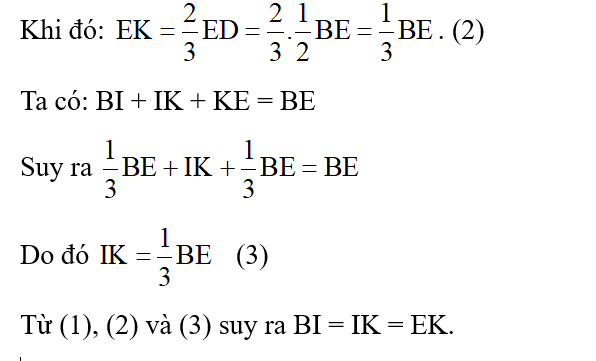10 câu hỏi trắc nghiệm thuộc Dạng 1. Nhận biết trung tuyến, trọng tâm tam giác và sử dụng tính chất trọng tâm của tam giác

Trắc nghiệm Toán 7 Bài 34: Sự đồng quy của ba đường trung tuyến, ba đường phân giác trong một tam giác có đáp án

Dạng 1. Nhận biết trung tuyến, trọng tâm tam giác và sử dụng tính chất trọng tâm của tam giác

474 lượt thi
10 câu hỏi
0 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Khẳng định nào sau đây là sai?

A. Trong một tam giác có ba đường trung tuyến;

B. Các đường trung tuyến của tam giác cắt nhau tại một điểm;

C. Giao của ba đường trung tuyến của một tam giác gọi là trọng tâm của tam giác đó;

D. Một tam giác có hai trọng tâm.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D

Trong một tam giác chỉ có một trọng tâm nên D sai.

Câu 2:

Điền số thích hợp vào chỗ trống: “Trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng … độ dài đường trung tuyến đi qua đỉnh ấy”.

A. $\frac{2}{3}$ ;

B. $\frac{3}{2}$ ;

C. 3;

D. 2.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A

Theo tính chất, trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng $\frac{2}{3}$ độ dài đường trung tuyến đi qua đỉnh ấy.

Câu 3:

Tam giác ABC có trung tuyến AM = 9 cm và G là trọng tâm. Độ dài đoạn AG là:

A. 4,5 cm;

B. 3 cm;

C. 6 cm;

D. 4 cm.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C

Vì G là trọng tâm tam giác ABC và AM là đường trung tuyến nên $A G = \frac{2}{3} A M$ (tính chất trọng tâm của tam giác)

Do đó $A G = \frac{2}{3} .9 = 6$ (cm).

Câu 4:

Cho hình vẽ sau:

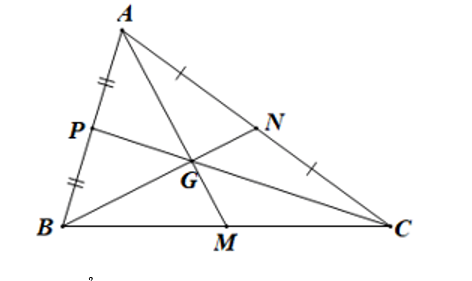
Biết AM = 3 cm. Độ dài đoạn thẳng GM là:

A. 1 cm;

B. 2 cm;

C. 3 cm;

D. 4,5 cm.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A

Trên hình vẽ, hai đường trung tuyến BN và CP cắt nhau tại G nên G là trọng tâm ΔABC.

Do đó $A G = \frac{2}{3} A M$ (tính chất trọng tâm).

Suy ra $G M = \frac{1}{3} A M = \frac{1}{3} \cdot 3 = 1 (cm)$ .

Câu 5:

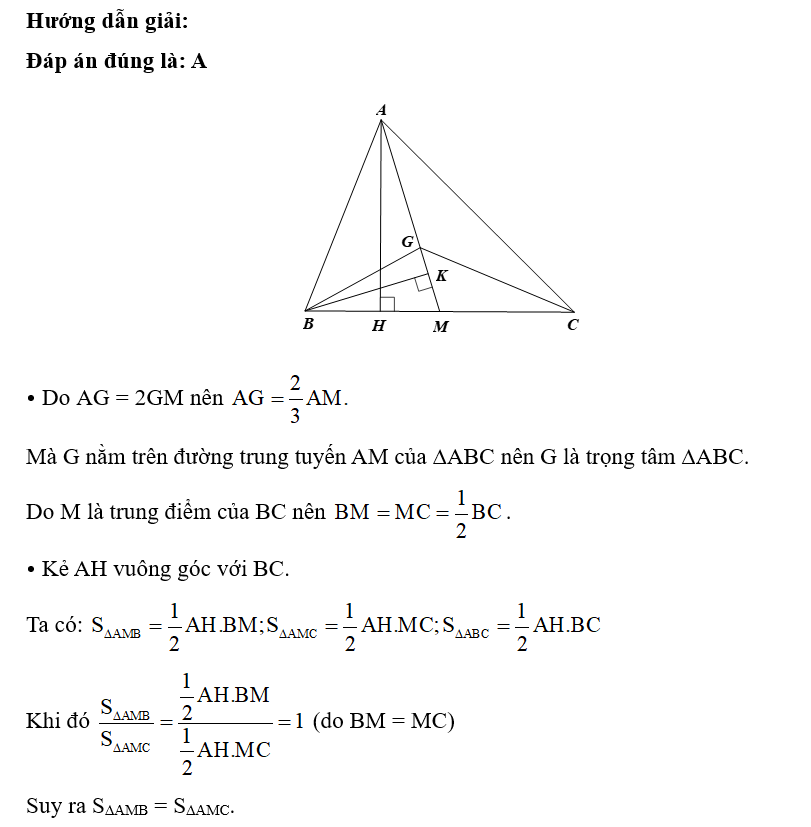
Cho ∆ABC có G là trọng tâm như hình vẽ.

Cho tam giác ABC có G là trọng tâm như hình vẽ. Biết AG = 4x + 6 và AM = 9x. (ảnh 1)

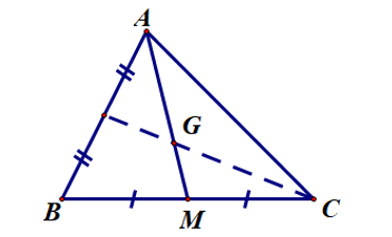
Biết AG = 4x + 6 và AM = 9x. Giá trị của x là

A. x = 4;

B. x = 1;

C. x = 2;

D. x = 3.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D

Ta có G là trọng tâm của ∆ABC.

Suy ra $A G = \frac{2}{3} A M$ .

Do đó $4 x + 6 = \frac{2}{3} .9 x$ .

4x + 6 = 2.3x

4x + 6 = 6x

4x – 6x = –6

–2x = –6.

x = –6 : (–2)

x = 3.

Câu 6:

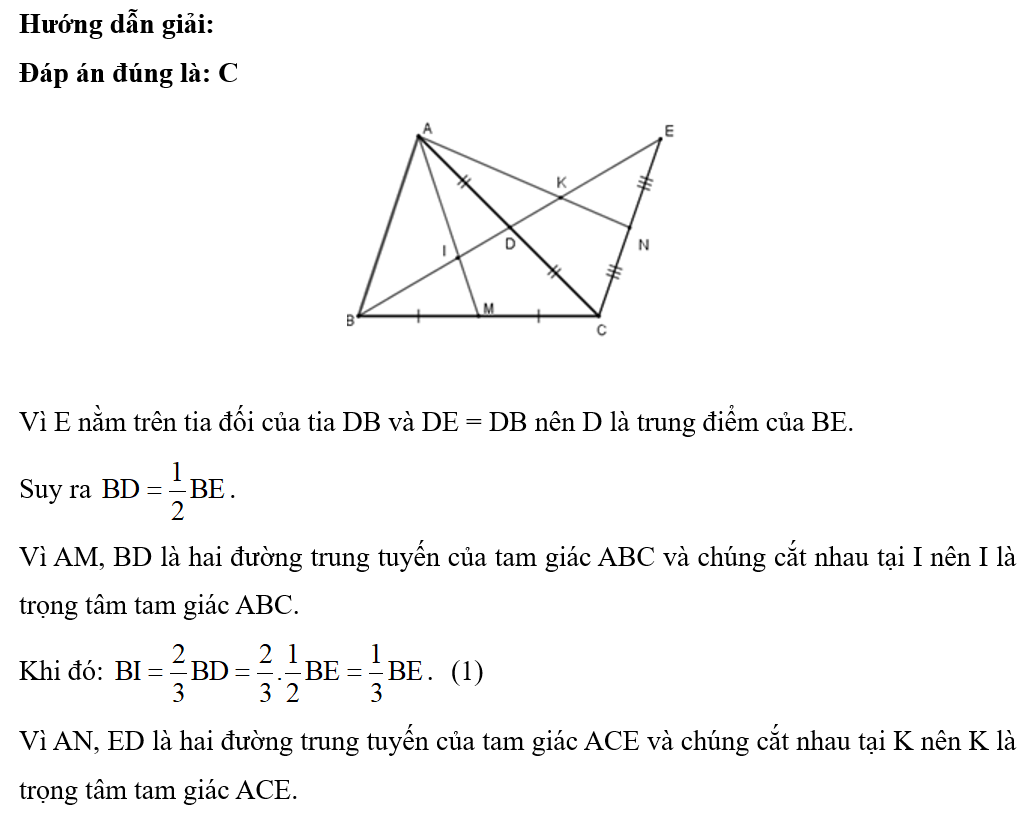
Cho ∆ABC có đường trung tuyến AD. Trên đoạn thẳng AD lấy hai điểm E, G sao cho AG = GE = ED. Trọng tâm của ∆ABC là điểm:

A. B;

B. E;

C. G;

D. D.

Xem đáp án

Hướng dẫn giải:

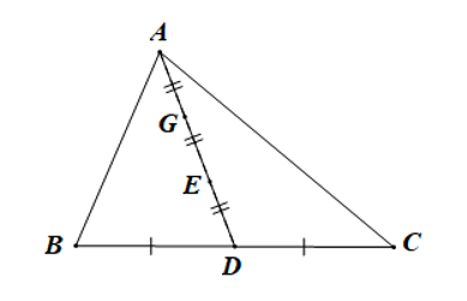
Cho tam giác ABC có đường trung tuyến AD. Trên đoạn thẳng AD lấy hai điểm E, G sao (ảnh 1)

Đáp án đúng là: B

Ta có AD = AG + GE + ED = AG + AG + AG = 3AG.

Suy ra $A G = G E = E D = \frac{1}{3} A D$ .

Ta có $A E = A G + G E = \frac{1}{3} A D + \frac{1}{3} A D = \frac{2}{3} A D$ .

Mà AD là đường trung tuyến của ∆ABC.

Do đó E là trọng tâm của ∆ABC.

Câu 7:

Cho ∆ABC có ba đường trung tuyến AX, BY, CZ cắt nhau tại G. Biết GA = GB = GC. Khẳng định nào sau đây là đúng?

A. GX > GY > GZ;

B. GX = GY = GZ;

C. GX < GY = GZ;

D. GX = GY > GZ.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B

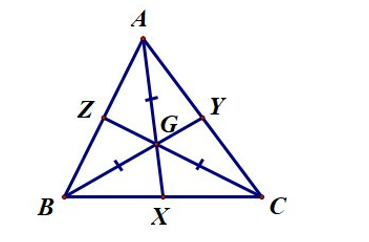
Cho tam giác ABC có ba đường trung tuyến AX, BY, CZ cắt nhau tại G. Biết GA = GB = GC. Khẳng định nào sau đây là đúng? (ảnh 1)

Vì G là trọng tâm của ∆ABC nên từ tính chất trọng tâm ta có:

$\frac{G X}{G A} = \frac{1}{2}, \frac{G Y}{G B} = \frac{1}{2}, \frac{G Z}{G C} = \frac{1}{2} .$

Suy ra $G X = \frac{1}{2} G A, G Y = \frac{1}{2} G B, G Z = \frac{1}{2} G C .$

Mà GA = GB = GC (giả thiết)

Suy ra GX = GY = GZ.

Câu 8:

Cho tam giác ABC, các đường trung tuyến BD và CE. Khẳng định nào sau đây là đúng?

A. $B D + C E < \frac{3}{2} B C$ ;

B. $B D + C E > \frac{3}{2} B C$ ;

C. $B D + C E = \frac{3}{2} B C$ ;

B D + C E = B C

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B

Gọi G là giao điểm của BD và CE. Khi đó G là trọng tâm của tam giác ABC.

Trong ΔGBC ta có BG + CG > BC.

Ta lại có $B G = \frac{2}{3} B D; C G = \frac{2}{3} C E$ (tính chất trọng tam của tam giác).

Từ đó $\frac{2}{3} B D + \frac{2}{3} C E > B C$

Suy ra $\frac{2}{3} (B D + C E) > B C$

Do đó $B D + C E > \frac{3}{2} B C .$

Câu 9:

Cho tam giác ABC, đường trung tuyến BD. Trên tia đối của tia DB lấy điểm E sao cho DE = DB. Gọi M, N theo thứ tự là trung điểm của BC; CE. Gọi I; K theo thứ tự là giao điểm của AM, AN và BE. Khẳng định nào sau đây là đúng?

A. BI = IK > KE;

B. BI > IK > KE;

C. BI = IK = KE;

D. BI < IK < KE.

Xem đáp án