10 câu hỏi trắc nghiệm thuộc Dạng 6: Chứng minh ba điểm thẳng hàng có đáp án

Câu 1:

Cho tam giác ABC có trọng tâm G, lấy các điểm I, J thỏa mãn: $\vec{I A} = 2 \vec{I B}$ , $3 \vec{J A} + 2 \vec{J C} = \vec{0}$ . Ba điểm nào sau đây thẳng hàng ?

A. A, B, G;

B. A, C, G;

C. A, I, G;

D. I, J, G.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D.

+ Vì G là trọng tâm tam giác ABC nên G nằm trong tam giác ABC, do đó ba điểm A, B, G và A, C, G không thể thẳng hàng.

+ Vì $\vec{I A} = 2 \vec{I B}$ nên A, I, B thẳng hàng và I không phải trung điểm AB nên A, I, G không thẳng hàng.

+ Ta có: G là trọng tâm tam giác ABC nên:

$\vec{J A} + \vec{J B} + \vec{J C} = 3 \vec{J G}$

$\Leftrightarrow 2 \vec{J A} + 2 \vec{J B} + 2 \vec{J C} = 6 \vec{J G}$

Mà: $3 \vec{J A} + 2 \vec{J C} = \vec{0} \Rightarrow 2 \vec{J C} = - 3 \vec{J A}$

Nên: $2 \vec{J A} + 2 \vec{J B} - 3 \vec{J A} = 6 \vec{J G}$

$\Leftrightarrow 2 \vec{J B} = 6 \vec{J G} + \vec{J A}$

Mặt khác: $\vec{I A} = 2 \vec{I B} \Leftrightarrow \vec{I J} + \vec{J A} = 2 \vec{I J} + 2 \vec{J B}$

Mà $2 \vec{J B} = 6 \vec{J G} + \vec{J A}$ nên ta lại có:

$\vec{I J} + \vec{J A} = 2 \vec{I J} + 6 \vec{J G} + \vec{J A}$

$\Leftrightarrow \vec{I J} = - 6 \vec{J G}$

Vậy I, J, G thẳng hàng.

Câu 2:

Cho tam giác ABC, lấy các điểm M, N, P thỏa mãn: $\vec{M A} + \vec{M B} = \vec{0}$ , $3 \vec{A N} - 2 \vec{A C} = \vec{0}$ , $\vec{P B} = 2 \vec{P C}$ . Ba điểm nào sau đây thẳng hàng ?

A. M, N, P;

B. A, M, B;

C. A, N, C;

D. M, N, B.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A.

Ta có:

$3 \vec{A N} - 2 \vec{A C} = \vec{0}$

$\Leftrightarrow 3 \vec{A M} + 3 \vec{M N} - 2 \vec{A P} - 2 \vec{P C} = \vec{0}$ (quy tắc ba điểm)

$\Leftrightarrow \vec{A M} + 3 \vec{M N} + 2 \vec{P M} - 2 \vec{P C} = \vec{0}$

Mà: $\vec{A M} = \vec{M B}$ và $2 \vec{P C} = \vec{P B}$ nên ta có:

$\vec{A M} + 3 \vec{M N} + 2 \vec{P M} - 2 \vec{P C} = \vec{0}$

$\Leftrightarrow \vec{M B} + 3 \vec{M N} + 2 \vec{P M} + \vec{B P} = 0$

$\Leftrightarrow \vec{M P} + 3 \vec{M N} + 2 \vec{P M} = 0$

$\Leftrightarrow 3 \vec{M N} = \vec{M P}$ .

Vậy M, N, P thẳng hàng.

Câu 3:

Cho điểm A, B, C sao cho: $\vec{C A} - 2 \vec{C B} = \vec{0}$ . Cho điểm M bất kỳ trong mặt phẳng và gọi $\vec{M N}$ là vectơ định bởi $\vec{M N} = \vec{M A} - 2 \vec{M B}$ . Ba điểm nào sau đây thẳng hàng ?

A. M, N, A;

B. M, B, A;

C. M, N, C;

D. A, N, B.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C.

Ta có:

$\vec{C A} - 2 \vec{C B} = \vec{0} \Leftrightarrow \vec{C A} - \vec{C B} = \vec{C B} \Leftrightarrow \vec{B A} = \vec{C B}$

$\Leftrightarrow \vec{B C} + \vec{C A} = \vec{C B} \Leftrightarrow \vec{C A} - 2 \vec{C B} = \vec{0}$

Mặt khác ta có:

$\begin{array}{l} \vec{M N} = \vec{M A} - 2 \vec{M B} \\ = \vec{M C} + \vec{C A} - 2 (\vec{M C} + \vec{C B}) \\ = - \vec{M C} + (\vec{C A} - 2 \vec{C B}) \\ = - \vec{M C} \end{array}$

$\Rightarrow \vec{M N} = - \vec{M C}$

Vậy M, N, C thẳng hàng.

Câu 4:

Cho hình bình hành ABCD. Trên đoạn BC lấy điểm H, trên đoạn BD lấy điểm K sao cho: BH = CH, DK = 2BK. Ba điểm nào sau đây thẳng hàng ?

A. A, K, H;

B. A, B, C;

C. A, K, C;

D. B, K, H.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A.

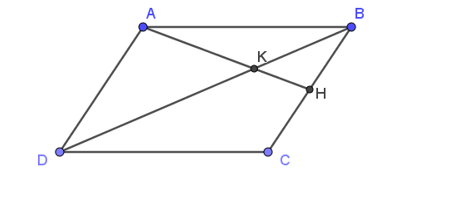
Cho hình bình hành ABCD. Trên đoạn BC lấy điểm H, trên đoạn BD lấy điểm K (ảnh 1)

Ta có:

$\vec{A K} = \vec{A B} + \vec{B K} = \vec{A B} + \frac{1}{3} \vec{B D} = \vec{A B} + \frac{1}{3} (\vec{A D} - \vec{A B}) = \frac{2}{3} \vec{A B} + \frac{1}{3} \vec{A D}$

$\Rightarrow 3 \vec{A K} = 2 \vec{A B} + \vec{A D}$ (1)

Lại có: $\vec{A H} = \vec{A B} + \vec{B H} = \vec{A B} + \frac{1}{2} \vec{B C}$

Do ABCD là hình bình hành nên ta có: $\vec{B C} = \vec{A D}$

Do đó, ta có: $\vec{A H} = \vec{A B} + \frac{1}{2} \vec{A D} \Rightarrow 2 \vec{A H} = 2 \vec{A B} + \vec{A D}$ (2)

Từ (1) và (2) $\Rightarrow 3 \vec{A K} = 2 \vec{A H} \Leftrightarrow \vec{A K} = \frac{2}{3} \vec{A H}$

Vậy A, K, H thẳng hàng.

Câu 5:

Cho hình bình hành ABCD. Trên BC lấy điểm H, trên BD lấy điểm K sao cho: $\vec{B H} = \frac{1}{5} \vec{B C}$ , $\vec{B K} = \frac{1}{6} \vec{B D}$ . Ba điểm nào sau đây thẳng hàng ?

A. A, K, H;

B. A, B, C;

C. A, K, C;

D. B, K, H.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A.

Ta có:

$\vec{A K} = \vec{A B} + \vec{B K} = \vec{A B} + \frac{1}{6} \vec{B D} = \vec{A B} + \frac{1}{6} (\vec{A D} - \vec{A B}) = \frac{5}{6} \vec{A B} + \frac{1}{6} \vec{A D}$

$\Rightarrow 6 \vec{A K} = 5 \vec{A B} + \vec{A D}$ (1)

\vec{A H} = \vec{A B} + \vec{B H} = \vec{A B} + \frac{1}{5} \vec{B C}

Do ABCD là hình bình hành nên ta có: $\vec{B C} = \vec{A D}$

Do đó, ta có: $\vec{A H} = \vec{A B} + \frac{1}{5} \vec{A D} \Rightarrow 5 \vec{A H} = 5 \vec{A B} + \vec{A D}$ (2)

Từ (1) và (2) $\Rightarrow 6 \vec{A K} = 5 \vec{A H} \Leftrightarrow \vec{A K} = \frac{5}{6} \vec{A H}$

Vậy A, K, H thẳng hàng.

Câu 6:

Cho tam giác ABC có M, N, P thỏa mãn: $\vec{M B} = 3 \vec{M C}$ , $\vec{N A} + 3 \vec{N C} = \vec{0}$ , $\vec{P A} + \vec{P B} = \vec{0}$ . Ba điểm nào sau đây thẳng hàng ?

A. A, B, C;

B. M, N, A;

C. M, N, P;

D. B, N, C.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C.

Ta có:

$\vec{P A} + \vec{P B} = \vec{0} \Leftrightarrow - \vec{A P} + \vec{P B} = 0 \Leftrightarrow - \vec{A P} + \vec{A B} - \vec{A P} = \vec{0} \Leftrightarrow \vec{A P} = \frac{1}{2} \vec{A B}$

$\vec{N A} + 3 \vec{N C} = \vec{0} \Leftrightarrow - \vec{A N} + 3 (\vec{A C} - \vec{A N}) = \vec{0} \Leftrightarrow 4 \vec{A N} = 3 \vec{A C} \Leftrightarrow \vec{A N} = \frac{3}{4} \vec{A C}$

$\vec{M B} = 3 \vec{M C} \Leftrightarrow \vec{A B} - \vec{A M} = 3 (\vec{A C} - \vec{A M}) \Leftrightarrow 2 \vec{A M} = 3 \vec{A C} - \vec{A B} \Leftrightarrow \vec{A M} = \frac{3}{2} \vec{A C} - \frac{1}{2} \vec{A B}$

Do đó, có:

$\vec{M P} = \vec{A P} - \vec{A M} = \frac{1}{2} \vec{A B} - \frac{3}{2} \vec{A C} + \frac{1}{2} \vec{A B} = \vec{A B} - \frac{3}{2} \vec{A C}$

$\vec{M N} = \vec{A N} - \vec{A M} = \frac{3}{4} \vec{A C} - \frac{3}{2} \vec{A C} + \frac{1}{2} \vec{A B} = \frac{1}{2} \vec{A B} - \frac{3}{4} \vec{A C}$

$\Rightarrow \vec{M P} = 2 \vec{M N}$

Vậy M, N, P thẳng hàng.

Câu 7:

Cho tam giác ABC có trọng tâm G và điểm I sao cho: $\vec{I C} - \vec{I B} + \vec{I A} = \vec{0}$ . Ba điểm nào sau đây thẳng hàng ?

A. I, G, C;

B. I, G, A;

C. I, A, B;

D. I, G, B.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D.

Ta có: G là trọng tâm tam giác ABC nên có:

$\vec{I A} + \vec{I B} + \vec{I C} = 3 \vec{I G} \Leftrightarrow \vec{I A} + \vec{I C} = 3 \vec{I G} - \vec{I B}$

Theo bài ra ta có: $\vec{I C} - \vec{I B} + \vec{I A} = \vec{0}$

$\Leftrightarrow (\vec{I C} + \vec{I A}) - \vec{I B} = \vec{0}$

$\Leftrightarrow 3 \vec{I G} - \vec{I B} - \vec{I B} = \vec{0}$

$\Leftrightarrow 3 \vec{I G} = 2 \vec{I B} \Leftrightarrow \vec{I G} = \frac{2}{3} \vec{I B}$

Vậy I, G, B thẳng hàng.

Câu 8:

Cho tam giác ABC có điểm I nằm trên cạnh AC sao cho $\vec{B I} = \frac{3}{4} \vec{A C} - \vec{A B}$ , J là điểm thỏa mãn $\vec{B J} = \frac{1}{2} \vec{A C} - \frac{2}{3} \vec{A B}$ . Ba điểm nào sau đây thẳng hàng ?

A. I, J, C;

B. I, J, B;

C. I, A, B;

D. I, G, B.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B.

Ta có: $\vec{B J} = \frac{1}{2} \vec{A C} - \frac{2}{3} \vec{A B}$

$\vec{B I} = \frac{3}{4} \vec{A C} - \vec{A B} = \frac{3}{2} . \frac{1}{2} \vec{A C} - \frac{3}{2} . \frac{2}{3} \vec{A B} = \frac{3}{2} (\frac{1}{2} \vec{A C} - \frac{2}{3} \vec{A B}) = \frac{3}{2} \vec{B J}$

Do đó, $\vec{B I} = \frac{3}{2} \vec{B J}$

Vậy B, I, J thẳng hàng.

Câu 9:

Cho tam giác ABC có điểm D sao cho: $\vec{B D} = \frac{2}{3} \vec{B C}$ và I là trung điểm của AD. Gọi M là điểm thỏa mãn $\vec{A M} = x \vec{A C}$ với x là số thực. Để B, I, M thẳng hàng thì x = ?

A. 1;

B. 2;

C.

\frac{5}{2}

;

D.

\frac{2}{5}

.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D.

Vì I là trung điểm AD nên có:

$\vec{B I} = \frac{1}{2} (\vec{B A} + \vec{B D}) = \frac{1}{2} (\vec{B A} + \frac{2}{3} \vec{B C}) = \frac{1}{2} \vec{B A} + \frac{1}{3} \vec{B C}$

$\vec{A M} = x \vec{A C} \Leftrightarrow \vec{B M} - \vec{B A} = x (\vec{B C} - \vec{B A}) \Leftrightarrow \vec{B M} = (1 - x) \vec{B A} + x \vec{B C}$

Ba điểm B, I, M thẳng hàng khi và chỉ khi tồn tại số thực k sao cho

$\vec{B M} = k \vec{B I}$

$\Leftrightarrow (1 - x) \vec{B A} + x \vec{B C} = \frac{k}{2} \vec{B A} + \frac{k}{3} \vec{B C}$

$\Leftrightarrow (1 - x - \frac{k}{2}) \vec{B A} + (x - \frac{k}{3}) \vec{B C} = \vec{0}$

$\Leftrightarrow \{\begin{cases} 1 - x - \frac{k}{3} = 0 \\ x - \frac{k}{2} = 0 \end{cases}$

$\Leftrightarrow \{\begin{cases} x = \frac{2}{5} \\ k = \frac{6}{5} \end{cases}$

Vậy x = $\frac{2}{5}$ thì thỏa mãn yêu cầu bài toán.

Câu 10:

Cho hình bình hành ABCD, I là trung điểm của cạnh BC và E là điểm thuộc đường chéo AC sao cho 3AE = 2AC. Ba điểm nào sau đây thẳng hàng ?

A. D, E, I;

B. D, E, C;

C. A, I, E.

D. D, E, A;

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A.

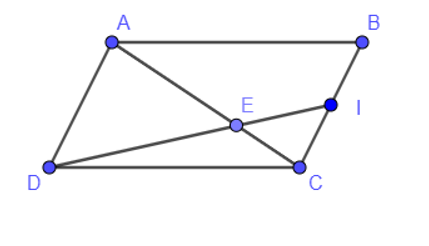
Cho hình bình hành ABCD, I là trung điểm của cạnh BC và E là điểm thuộc đường (ảnh 1)

Ta có: $\vec{D I} = \vec{D C} + \vec{C I} \Leftrightarrow \vec{D I} = \vec{D C} + \frac{1}{2} \vec{C B}$ (1)

Lại có: $\vec{C E} = \frac{1}{3} \vec{C A} = \frac{1}{3} (\vec{C D} + \vec{D A}) = \frac{1}{3} (\vec{C D} + \vec{C B})$

Và $\vec{D E} = \vec{D C} + \vec{C E} = \vec{D C} + \frac{1}{3} \vec{C D} + \frac{1}{3} \vec{C B} = \frac{2}{3} \vec{D C} + \frac{1}{3} \vec{C B} = \frac{2}{3} (\vec{D C} + \frac{1}{2} \vec{C B})$ (2)

Từ (1) và (2) $\Rightarrow \vec{D E} = \frac{2}{3} \vec{D I}$

Vậy D, E, I thẳng hàng.

Trắc nghiệm Toán 10 CTST Bài 3. Tích của một số với một vectơ có đáp án

Dạng 6: Chứng minh ba điểm thẳng hàng có đáp án

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương