10 câu hỏi trắc nghiệm thuộc Dạng 4: Phân tích một vectơ thành hai hay nhiều vectơ cho trước có đáp án

Câu 1:

Cho tam giác ABC. Đặt $\vec{A B} = \vec{a}$ , $\vec{A C} = \vec{b}$ . M thuộc cạnh AB sao cho AB = 3AM, N thuộc tia BC và CN = 2BC. Phân tích $\vec{A N}$ qua các vectơ $\vec{a}$ và $\vec{b}$ ta được biểu thức là:

A. $2 \vec{a} + 3 \vec{b}$

B. $- 2 \vec{a} + 3 \vec{b}$

C. $2 \vec{a} - 3 \vec{b}$

D. $2 \vec{a} + \vec{b}$

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B.

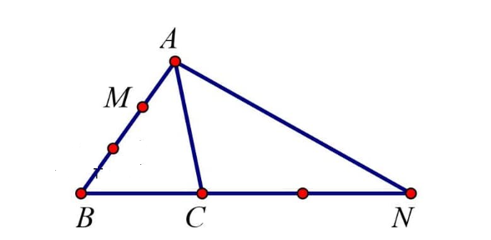
Cho tam giác ABC. Đặt vecto AB= vecto a,vecto AC= vecto b . M thuộc cạnh AB sao cho AB = 3AM, (ảnh 1)

Theo đề bài: CN = 2BC nên $\vec{B N} = 3 \vec{B C}$

Ta có:

$\vec{A N} = \vec{A B} + \vec{B N} = \vec{A B} + 3 \vec{B C} = \vec{A B} + 3 (\vec{A C} - \vec{A B}) = - 2 \vec{A B} + 3 \vec{A C} = - 2 \vec{a} + 3 \vec{b}$ .

Câu 2:

Cho tam giác ABC. Đặt $\vec{A B} = \vec{a}$ , $\vec{A C} = \vec{b}$ . M thuộc cạnh AB sao cho AB = 3AM, N thuộc tia BC và CN = 2BC. Phân tích $\vec{M N}$ qua các vectơ $\vec{a}$ và $\vec{b}$ ta được biểu thức là:

A. $- \frac{7}{3} \vec{a} + 3 \vec{b}$

B. $- \frac{1}{3} \vec{a} + 3 \vec{b}$

C. $- \frac{2}{3} \vec{a} + 3 \vec{b}$

D. $- \frac{5}{3} \vec{a} + 3 \vec{b}$

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A.

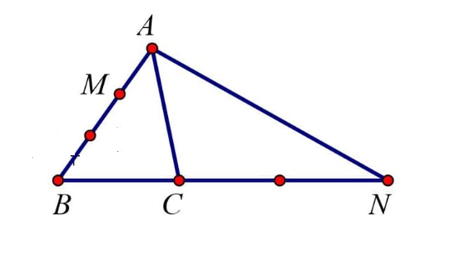
Theo đề bài:

AB = 3AM nên $\vec{A M} = \frac{1}{3} \vec{A B} \Rightarrow \vec{M A} = - \frac{1}{3} \vec{A B}$

CN = 2BC nên $\vec{B N} = 3 \vec{B C}$

Ta có:

$\vec{A N} = \vec{A B} + \vec{B N} = \vec{A B} + 3 \vec{B C} = \vec{A B} + 3 (\vec{A C} - \vec{A B}) = - 2 \vec{A B} + 3 \vec{A C} = - 2 \vec{a} + 3 \vec{b}$

$\vec{M N} = \vec{M A} + \vec{A N} = - \frac{1}{3} \vec{a} - 2 \vec{a} + 3 \vec{b} = - \frac{7}{3} \vec{a} + 3 \vec{b}$ .

Câu 3:

Cho tam giác ABC, trên cạnh BC lấy M sao cho BM = 3CM, trên đoạn AM lấy N sao cho 2AN = 5MN. Phân tích vectơ $\vec{B N}$ qua các vectơ $\vec{A B}$ và $\vec{A C}$ .

A. $\vec{B N}$ = $\frac{23}{28} \vec{A B} + \frac{15}{28} \vec{A C}$ ;

B.

\vec{B N}

=

- \frac{23}{28} \vec{A B} - \frac{15}{28} \vec{A C}

;

C.

\vec{B N}

=

- \frac{23}{28} \vec{A B} + \frac{15}{28} \vec{A C}

;

D.

\vec{B N}

=

\frac{23}{28} \vec{A B} - \frac{15}{28} \vec{A C}

.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C.

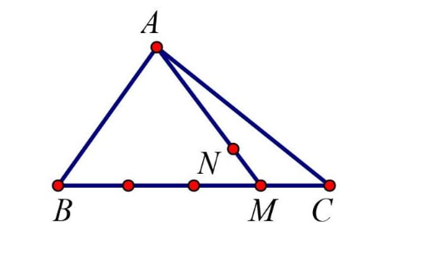
Cho tam giác ABC, trên cạnh BC lấy M sao cho BM = 3CM, trên đoạn AM lấy N (ảnh 1)

Theo đề bài ta có:

$\vec{B M} = \frac{3}{4} \vec{B C}$ và $\vec{A N} = \frac{5}{7} \vec{A M}$

Ta có:

$\vec{A M} = \vec{A B} + \vec{B M} = \vec{A B} + \frac{3}{4} \vec{B C} = \vec{A B} + \frac{3}{4} (\vec{A C} - \vec{A B}) = \frac{1}{4} \vec{A B} + \frac{3}{4} \vec{A C}$

$\vec{B N} = \vec{B A} + \vec{A N} = - \vec{A B} + \frac{5}{7} \vec{A M} = - \vec{A B} + \frac{5}{7} (\frac{1}{4} \vec{A B} + \frac{3}{4} \vec{A C}) = - \frac{23}{28} \vec{A B} + \frac{15}{28} \vec{A C}$

Câu 4:

Cho tam giác ABC, G là trọng tâm của tam giác ABC. Phân tích vectơ $\vec{G C}$ qua các vectơ $\vec{G A}$ và $\vec{G B}$ .

A. $\vec{G C}$ = $\vec{G A} + \vec{G B}$ ;

B.

\vec{G C}

=

- \vec{G A} - \vec{G B}

;

C.

\vec{G C}

=

- \vec{G A} + \vec{G B}

;

D.

\vec{G C}

=

\vec{G A} - \vec{G B}

.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B.

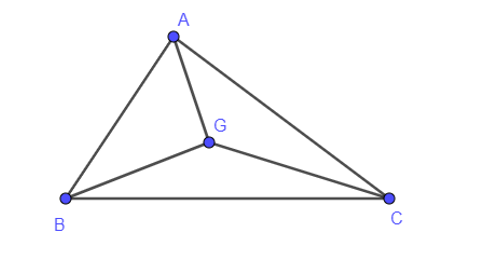
Cho tam giác ABC, G là trọng tâm của tam giác ABC. Phân tích vectơ vecto GC (ảnh 1)

Theo đề bài ta có: G là trọng tâm của tam giác ABC nên

$\vec{G A} + \vec{G B} + \vec{G C} = \vec{0} \Leftrightarrow \vec{G C} = - \vec{G A} - \vec{G B}$ .

Câu 5:

Cho tam giác ABC, trên cạnh BC lấy M sao cho BM = 3CM, trên đoạn AM lấy N sao cho 2AN = 5MN. G là trọng tâm của tam giác ABC. Phân tích vectơ $\vec{M N}$ qua các vectơ $\vec{G A}$ và $\vec{G B}$ .

A. $\vec{M N}$ = $\frac{1}{2} \vec{G A} + \frac{1}{7} \vec{G B}$ ;

B.

\vec{M N}

=

\frac{1}{7} \vec{G A} + \frac{1}{7} \vec{G B}

;

C.

\vec{M N}

=

\frac{2}{7} \vec{G A} - \frac{1}{7} \vec{G B}

;

D.

\vec{M N}

=

\frac{1}{2} \vec{G A} + \frac{2}{7} \vec{G B}

.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A.

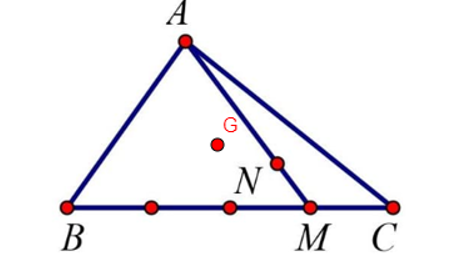
Cho tam giác ABC, trên cạnh BC lấy M sao cho BM = 3CM, trên đoạn AM lấy N sao (ảnh 1)

Theo đề bài ta có:

$\vec{B M} = \frac{3}{4} \vec{B C}$ và $\vec{M N} = - \frac{2}{7} \vec{A M}$ .

Vì G là trọng tâm tam giác ABC nên $\vec{G A} + \vec{G B} + \vec{G C} = \vec{0} \Leftrightarrow \vec{G C} = - \vec{G A} - \vec{G B}$

Ta có:

$\vec{A M} = \vec{A B} + \vec{B M} = \vec{A B} + \frac{3}{4} \vec{B C} = \vec{A B} + \frac{3}{4} (\vec{A C} - \vec{A B}) = \frac{1}{4} \vec{A B} + \frac{3}{4} \vec{A C}$

$\vec{M N} = - \frac{2}{7} \vec{A M} = - \frac{2}{7} (\frac{1}{4} \vec{A B} + \frac{3}{4} \vec{A C})$

$= - \frac{1}{14} (\vec{G B} - \vec{G A}) - \frac{3}{14} (\vec{G C} - \vec{G A})$

$= - \frac{1}{14} (\vec{G B} - \vec{G A}) - \frac{3}{14} (- \vec{G A} - \vec{G B} - \vec{G A})$

$= \frac{1}{2} \vec{G A} + \frac{1}{7} \vec{G B}$ .

Câu 6:

Cho hình bình hành ABCD. Gọi M, N lần lượt là hai điểm nằm trên hai cạnh AB và CD sao cho AB = 3AM, CD = 2CN. Biểu diễn vectơ $\vec{A N}$ qua các vectơ $\vec{A B}$ và $\vec{A C}$ .

A. $\vec{A N}$ = $- \vec{A C} + \frac{1}{2} \vec{A B}$ ;

B.

\vec{A N}

=

\vec{A C} + \frac{1}{2} \vec{A B}

;

C.

\vec{A N}

=

- \vec{A C} - \frac{1}{2} \vec{A B}

;

D.

\vec{A N}

=

\vec{A C} - \frac{1}{2} \vec{A B}

.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D.

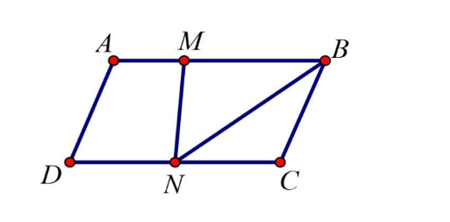
Cho hình bình hành ABCD. Gọi M, N lần lượt là hai điểm nằm trên hai cạnh AB và CD (ảnh 1)

Ta có: CD = 2CN và N nằm trên cạnh CD nên $\vec{C N} = \frac{1}{2} \vec{C D}$ .

Mà ABCD là hình bình hành nên $\vec{A B} = \vec{D C} \Leftrightarrow \vec{A B} = - \vec{C D}$ .

Do đó, $\vec{C N} = - \frac{1}{2} \vec{A B}$ .

Theo quy tắc ba điểm ta có: $\vec{A N} = \vec{A C} + \vec{C N} = \vec{A C} - \frac{1}{2} \vec{A B}$ .

Câu 7:

Cho hình bình hành ABCD. Gọi M, N lần lượt là hai điểm nằm trên hai cạnh AB và CD sao cho AB = 3AM, CD = 2CN và G là trọng tâm tam giác MNB. Phân tích vectơ $\vec{M N}$ qua các vectơ $\vec{A B}$ và $\vec{A C}$ .

A. $\vec{M N}$ = $\frac{5}{6} \vec{A B} - 2 \vec{A C}$ ;

B.

\vec{M N}

=

\frac{5}{6} \vec{A B} + \vec{A C}

;

C.

\vec{M N}

=

- \frac{5}{6} \vec{A B} + \vec{A C}

;

D.

\vec{M N}

=

- \frac{5}{6} \vec{A B} - \vec{A C}

.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C.

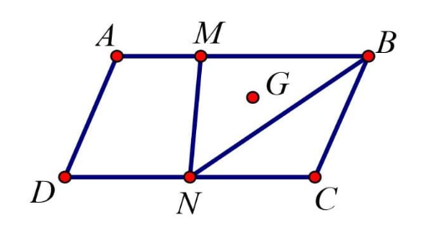
Vì AB = 3AM và M nằm trên cạnh AB nên $\vec{M A} = - \frac{1}{3} \vec{A B}$ .

Ta có: $\vec{A N} = \vec{A C} + \vec{C N} = \vec{A C} - \frac{1}{2} \vec{A B}$

Do đó ta có: $\vec{M N} = \vec{M A} + \vec{A N} = - \frac{1}{3} \vec{A B} + \vec{A C} - \frac{1}{2} \vec{A B} = - \frac{5}{6} \vec{A B} + \vec{A C}$ .

Câu 8:

Cho hình bình hành ABCD. Gọi M, N lần lượt là hai điểm nằm trên hai cạnh AB và CD sao cho AB = 3AM, CD = 2CN và G là trọng tâm tam giác MNB. Phân tích vectơ $\vec{A G}$ qua các vectơ $\vec{A B}$ và $\vec{A C}$ ta được $\vec{A G} = \frac{a}{b} \vec{A B} + \frac{c}{d} \vec{A C}$ với $\frac{a}{b}$ và $\frac{c}{d}$ là các phân số tối giản. Khi đó ta có: $\frac{a}{b} + \frac{c}{d} = ?$

A. $\frac{11}{18}$

B. $\frac{5}{18}$

C. $\frac{1}{3}$

D. $- \frac{1}{18}$

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A.

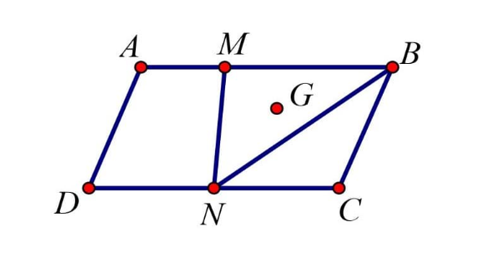
Vì AB = 3AM và M nằm trên cạnh AB nên $\vec{A M} = \frac{1}{3} \vec{A B}$ .

Ta có: $\vec{A N} = \vec{A C} + \vec{C N} = \vec{A C} - \frac{1}{2} \vec{A B}$ .

G là trọng tâm tam giác MNB nên ta có:

$3 \vec{A G} = \vec{A M} + \vec{A N} + \vec{A B} = \frac{1}{3} \vec{A B} + (\vec{A C} - \frac{1}{2} \vec{A B}) + \vec{A B} = \frac{5}{6} \vec{A B} + \vec{A C}$

$\Leftrightarrow \vec{A G} = \frac{5}{18} \vec{A B} + \frac{1}{3} \vec{A C}$ .

Do đó $\frac{a}{b} = \frac{5}{18}$ và $\frac{c}{d} = \frac{1}{3}$ .

Suy ra $\frac{a}{b} + \frac{c}{d} = \frac{5}{18} + \frac{1}{3} = \frac{11}{18}$ .

Câu 9:

Cho AK và BM là hai trung tuyến của tam giác ABC. Phân tích vectơ $\vec{A B}$ theo hai vectơ $\vec{A K} = \vec{u}$ và $\vec{B M} = \vec{v}$ ta được biểu thức là:

A. $\frac{2}{3} \vec{u} - \frac{1}{2} \vec{v}$ ;

B. $\frac{2}{3} \vec{u} + \frac{1}{2} \vec{v}$

C. $\frac{2}{3} \vec{u} - \frac{2}{3} \vec{v}$

D. $\frac{2}{3} \vec{u} + \frac{2}{3} \vec{v}$

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C.

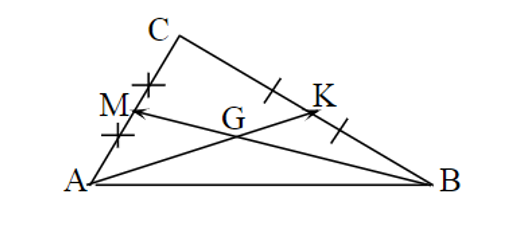
Cho AK và BM là hai trung tuyến của tam giác ABC. Phân tích vectơ AB theo hai (ảnh 1)

Ta có:

$\vec{A B} = \vec{A K} + \vec{K B} = \vec{A K} + \vec{K M} + \vec{M B}$

Mà $\vec{K M} = - \frac{1}{2} \vec{A B}$ (vì MK là đường trung bình của tam giác ABC)

Do đó:

$\vec{A B} = \vec{A K} - \frac{1}{2} \vec{A B} - \vec{B M}$

$\Leftrightarrow \vec{A B} + \frac{1}{2} \vec{A B} = \vec{A K} - \vec{B M}$

$\Leftrightarrow \frac{3}{2} \vec{A B} = \vec{A K} - \vec{B M}$

$\Leftrightarrow \vec{A B} = \frac{2}{3} \vec{A K} - \frac{2}{3} \vec{B M} = \frac{2}{3} \vec{u} - \frac{2}{3} \vec{v}$ .

Câu 10:

Cho tam giác ABC. Gọi I là điểm trên cạnh BC sao cho $2 \vec{I C} = 3 \vec{B I}$ . Phân tích vectơ $\vec{A I}$ theo hai vectơ $\vec{A B}$ và $\vec{A C}$ .

A. $\frac{3}{5} \vec{A B} + \frac{1}{5} \vec{A C}$ ;

B. $\frac{3}{5} \vec{A B} - \frac{1}{5} \vec{A C}$

C. $\frac{3}{5} \vec{A B} + \frac{2}{5} \vec{A C}$

D. $\frac{3}{5} \vec{A B} - \frac{2}{5} \vec{A C}$

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C.

Ta có: $2 \vec{I C} = 3 \vec{B I}$

$\Leftrightarrow 2 (\vec{A C} - \vec{A I}) = 3 (\vec{A I} - \vec{A B})$

$\Leftrightarrow 2 \vec{A C} - 2 \vec{A I} = 3 \vec{A I} - 3 \vec{A B}$

$\Leftrightarrow 5 \vec{A I} = 3 \vec{A B} + 2 \vec{A C}$

$\Leftrightarrow \vec{A I} = \frac{3}{5} \vec{A B} + \frac{2}{5} \vec{A C}$ .

Trắc nghiệm Toán 10 CTST Bài 3. Tích của một số với một vectơ có đáp án

Dạng 4: Phân tích một vectơ thành hai hay nhiều vectơ cho trước có đáp án

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương