10 câu hỏi trắc nghiệm thuộc Dạng 4: Chứng minh hai vectơ bằng nhau, hai vectơ đối nhau có đáp án

Câu 1:

Cho tam giác ABC có M, N lần lượt là trung điểm của AB và AC như hình vẽ.

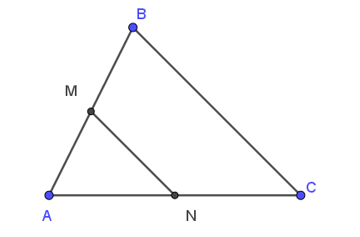
Vectơ nào bằng vectơ $\vec{N A}$ ?

A. $\vec{C N}$

B. $\vec{N B}$

C. $\vec{M N}$

D. $\vec{N C}$

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A.

Xét tam giác ABC có: N là trung điểm của AC, do đó: NA = CN $\Rightarrow |\vec{N A}| = |\vec{C N}|$

Ta có: $\vec{N A}$ và $\vec{C N}$ có cùng giá là đường thẳng AC.

Nên hai vectơ $\vec{N A}$ và $\vec{C N}$ cùng phương.

Mà $\vec{N A}$ và $\vec{C N}$ cùng hướng từ phải sang trái.

Vậy $\vec{N A}$ = $\vec{C N}$ .

Câu 2:

Cho tam giác ABC có M, N lần lượt là trung điểm của AB và AC. Vectơ nào là vectơ đối của vectơ $\vec{B M}$ ?

A. $\vec{C N}$

B. $\vec{N B}$

C. $\vec{A M}$

D. $\vec{A N}$

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C.

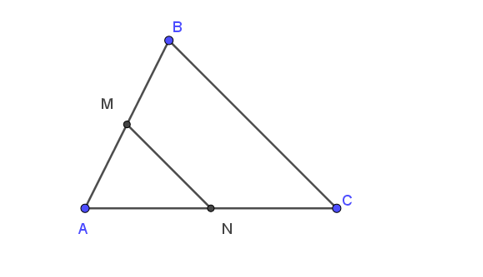
Cho tam giác ABC có M, N lần lượt là trung điểm của AB và AC. Vectơ nào (ảnh 1)

Xét tam giác ABC có: M là trung điểm của AB, do đó: AM = BM $\Rightarrow |\vec{B M}| = |\vec{A M}|$

Ta có: hai vectơ $\vec{B M}$ và $\vec{A M}$ có cùng giá là đường thẳng AB.

Mà $\vec{B M}$ có hướng từ phải sang trái và $\vec{A M}$ có hướng từ trái sang phải

Do đó, chúng ngược hướng.

Vậy hai vectơ $\vec{B M}$ và $\vec{A M}$ đối nhau.

Câu 3:

Cho tam giác ABC có M, N, P lần lượt là trung điểm các cạnh AB, AC, BC của tam giác ABC. Vectơ nào sau đây bằng vectơ $\vec{N C}$ .

A. $\vec{C N}$

B. $\vec{M P}$

C. $\vec{A M}$

D. $\vec{N A}$

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B.

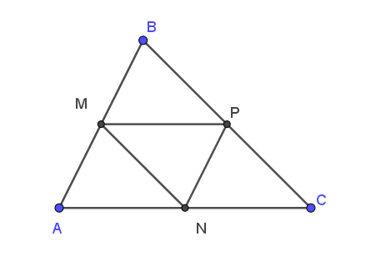
Cho tam giác ABC có M, N, P lần lượt là trung điểm các cạnh AB, AC, BC của tam giác ABC (ảnh 1)

Xét tam giác ABC có:

N là trung điểm của AC có: NC = $\frac{1}{2}$ AC (1)

M là trung điểm của AB, P là trung điểm của BC nên MP là đường trung bình của tam giác ABC, do đó: MP = $\frac{1}{2}$ AC (2), MP // AC (3)

Từ (1) và (2) ta suy ra: NC = MP hay $|\vec{N C}| = |\vec{M P}|$ .

Từ (3) ta có: hai vectơ $\vec{N C}$ và $\vec{M P}$ cùng phương, mà chúng cùng hướng đi từ trái sang phải.

Vậy $\vec{N C}$ = $\vec{M P}$ .

Câu 4:

Cho tam giác ABC có M, N, P lần lượt là trung điểm các cạnh AB, AC, BC của tam giác ABC. Vectơ nào sau đây là vectơ đối của $\vec{P N}$ .

A. $\vec{C N}$

B. $\vec{M N}$

C. $\vec{M P}$

D. $\vec{M B}$

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D.

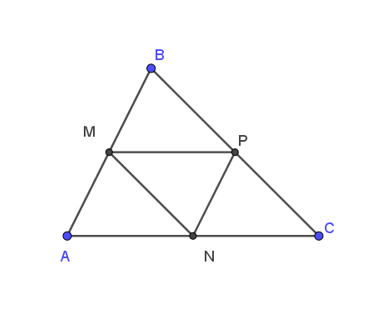
Cho tam giác ABC có M, N, P lần lượt là trung điểm các cạnh AB, AC, BC của tam giác (ảnh 1)

Xét tam giác ABC có:

M là trung điểm của AB có: MB = $\frac{1}{2}$ AB (1)

P là trung điểm của BC, N là trung điểm của AC nên PN là đường trung bình của tam giác ABC, do đó: PN = $\frac{1}{2}$ AB (2), PN // AB (3)

Từ (1) và (2) ta suy ra: MB = PN hay $|\vec{M B}| = |\vec{P N}|$

Từ (3) ta có: hai vectơ $\vec{P N}$ và $\vec{M B}$ cùng phương, mà chúng ngược hướng nhau.

Vậy hai vectơ $\vec{P N}$ và $\vec{M B}$ đối nhau.

Câu 5:

Cho hình vuông ABCD tâm O như hình vẽ sau:

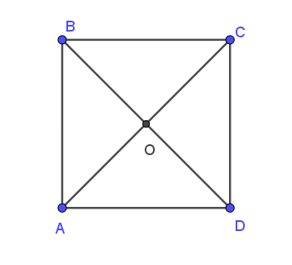
Vectơ nào sau đây bằng vectơ $\vec{O A}$ ?

A. $\vec{C O}$

B. $\vec{O D}$

C. $\vec{A O}$

D. $\vec{B O}$

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A.

Xét hình vuông ABCD tâm O có:

OA = CO = $\frac{1}{2}$ AC

$\Rightarrow |\vec{O A}| = |\vec{C O}|$ (1)

Mặt khác, $\vec{O A}$ và $\vec{C O}$ có cùng giá là đường thẳng AC

Do đó, $\vec{O A}$ và $\vec{C O}$ cùng phương, mà chúng cùng hướng (2)

Từ (1) và (2) ta kết luận: $\vec{C O}$ = $\vec{O A}$ .

Câu 6:

Cho hình vuông ABCD tâm O.

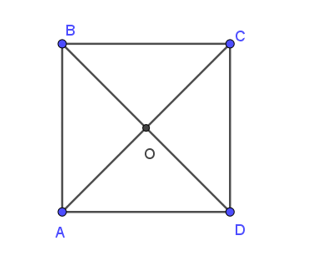
Khẳng định nào sau đây là đúng ?

A. $\vec{O C}$ = $\vec{O A}$ ;

B.

\vec{O D}

=

\vec{O A}

;

C.

\vec{B C} = \vec{D A}

;

D.

\vec{O B}

= –

\vec{O D}

.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D.

Xét hình vuông ABCD tâm O có:

OB = OD = $\frac{1}{2}$ BD

$\Rightarrow |\vec{O B}| = |\vec{O D}|$ (1)

Mặt khác, hai vectơ $\vec{O B}$ và $\vec{O D}$ có cùng giá là đường thẳng BD

Do đó, hai vectơ $\vec{O B}$ và $\vec{O D}$ cùng phương, mà chúng ngược hướng (2)

Từ (1) và (2) ta kết luận: $\vec{O B}$ = – $\vec{O D}$ .

Câu 7:

Cho hình vuông ABCD có tâm O. Các điểm Q, K, L, N lần lượt là trung điểm của AB, BC, CD, DA như hình vẽ.

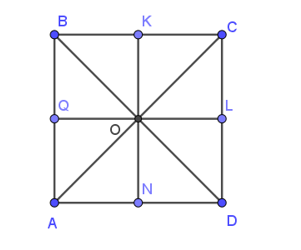
Cho hình vuông ABCD có tâm O. Các điểm Q, K, L, N lần lượt là trung điểm của AB (ảnh 1)

Khẳng định nào sau đây là đúng ?

A. $\vec{O Q} = \vec{K C}$

B. $\vec{O D} = \vec{O L}$

C. $\vec{K C} = \vec{A N}$

D. $\vec{O B} = \vec{O D}$

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C.

Xét hình vuông ABCD có:

BC // AD, do đó hai vectơ $\vec{K C}$ và $\vec{A N}$ cùng phương, mà chúng cùng hướng đi từ trái sang phải nên hai vectơ $\vec{K C}$ và $\vec{A N}$ cùng hướng (1).

Mặt khác: $K C = \frac{1}{2} B C$ (do K là trung điểm của BC); $A N = \frac{1}{2} A D$ (do N là trung điểm của AD).

Mà BC = AD (do ABCD là hình vuông)

$\Rightarrow K C = A N \Rightarrow |\vec{K C}| = |\vec{A N}|$ (2)

Từ (1) và (2) suy ra $\vec{K C} = \vec{A N}$ .

Câu 8:

Cho hình vuông ABCD có tâm O. Các điểm Q, K, L, N lần lượt là trung điểm của AB, BC, CD, DA như hình vẽ.

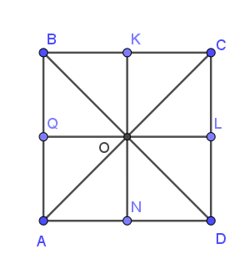
Khẳng định nào sau đây là sai ?

A. $\vec{O Q} = \vec{K C}$

B. $\vec{O D} = - \vec{O B}$

C. $\vec{K C} = \vec{A N}$

D. $\vec{O B} = - \vec{O D}$

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A.

Xét hình vuông ABCD có: Q là trung điểm của AB và L là trung điểm của CD.

Nên QL là đường trung bình của hình vuông ABCD.

Suy ra: BC //= QL và QL đi qua tâm O của hình vuông.

Do đó: $\vec{O Q}$ và $\vec{K C}$ cùng phương, mà chúng có hướng ngược nhau nên hai vectơ $\vec{O Q}$ và $\vec{K C}$ ngược hướng (1).

Mà: $K C = \frac{1}{2} B C$ ; $O Q = \frac{1}{2} Q L$ ; BC = QL.

$\Rightarrow K C = O Q \Rightarrow |\vec{K C}| = |\vec{O Q}|$ (2)

Từ (1) và (2) suy ra, $\vec{O Q} = - \vec{K C}$ , vậy A sai.

Câu 9:

Cho hình thoi ABCD tâm I như hình vẽ với E, F, G, H lần lượt là trung điểm của các cạnh AB, AD, CD, CB.

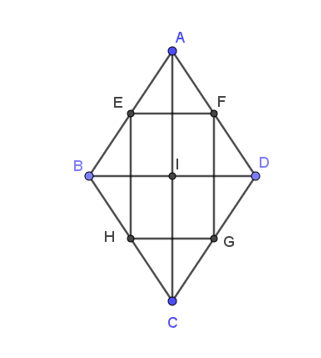
Cho hình thoi ABCD tâm I như hình vẽ với E, F, G, H lần lượt là trung điểm của (ảnh 1)

Khẳng định nào sau đây là đúng ?

A. $\vec{H G} = \vec{F E}$

B. $\vec{B E} = \vec{G D}$

C. $\vec{I C} = \vec{I A}$

D. $\vec{E F} = - \vec{H G}$

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B.

Xét hình thoi ABCD có:

AB = CD

Mà E là trung điểm của AB nên BE = $\frac{1}{2}$ AB

G là trung điểm của CD nên GD = $\frac{1}{2}$ CD

Do đó, BE = GD $\Rightarrow |\vec{B E}| = |\vec{G D}|$ (1)

Và: AB // CD

Do đó, $\vec{B E}, \vec{G D}$ cùng phương, hơn nữa chúng cùng hướng (2).

Từ (1) và (2) suy ra $\vec{B E} = \vec{G D}$ .

Câu 10:

Cho hình thoi ABCD tâm I như hình vẽ với E, F, G, H lần lượt là trung điểm của các cạnh AB, AD, CD, CB và J, L, K, M lần lượt là giao điểm của HE với BD, EF với AC, FG với BD, GH với AC.

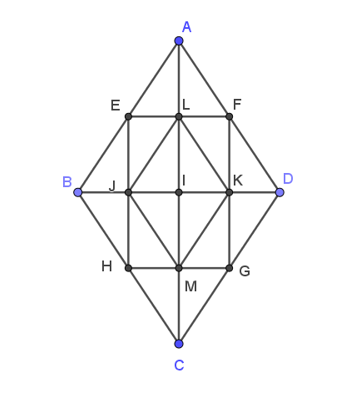
Cho hình thoi ABCD tâm I như hình vẽ với E, F, G, H lần lượt là trung điểm (ảnh 1)

Khẳng định nào sau đây là sai ?

A. $\vec{J L} \neq \vec{G D}$

B. $\vec{J L} = \vec{M K}$

C. $\vec{J L} = \vec{B E}$

D. $\vec{J L} \neq \vec{L K}$

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A.

Xét tam giác ABD có:

AB = AD (do ABCD là hình thoi)

Do đó, tam giác ABD cân tại A.

E là trung điểm của AB

F là trung điểm của AD

Do đó, EF là đường trung bình của tam giác ABD.

Lại có AI là đường cao của tam giác cân ABD (do I là giao hai đường chéo của hình thoi nên AC vuông góc với BD tại I)

Mà EF cắt AI tại L.

Từ đó ta suy ra L là trung điểm của AI.

Xét tam giác BAC có:

BA = BC (do ABCD là hình thoi)

Do đó, tam giác BAC cân.

E là trung điểm của AB

H là trung điểm của BC

Do đó, EH là đường trung bình của tam giác BAC.

Tương tự, BI là đường cao của tam giác BAC.

Mà EH cắt BI tại J

Từ đó suy ra J là trung điểm của BI.

Xét tam giác AIB có:

J là trung điểm của BI

L là trung điểm của AI

Do đó, JL là đường trung bình của tam giác AIB

$\Rightarrow J L = \frac{1}{2} A B$ (1), JL // AB (2)

Xét hình thoi ABCD có:

AB = CD (3)

AB // CD (4)

Do G là trung điểm của CD nên ta có: $G D = \frac{1}{2} C D$ (5)

Từ (1), (3), (5) ta suy ra: JL = GD nên $|\vec{J L}| = |\vec{G D}|$ (6)

Từ (2), (4) và (6) ta suy ra: $\vec{J L} = \vec{G D}$ (do chúng cùng phương, cùng hướng và có độ dài bằng nhau).

Vậy A sai.

Trắc nghiệm Toán 10 CTST Bài 1: Xác định vectơ. Tìm điểm đầu, điểm cuối, giá của vectơ có đáp án

Dạng 4: Chứng minh hai vectơ bằng nhau, hai vectơ đối nhau có đáp án

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương