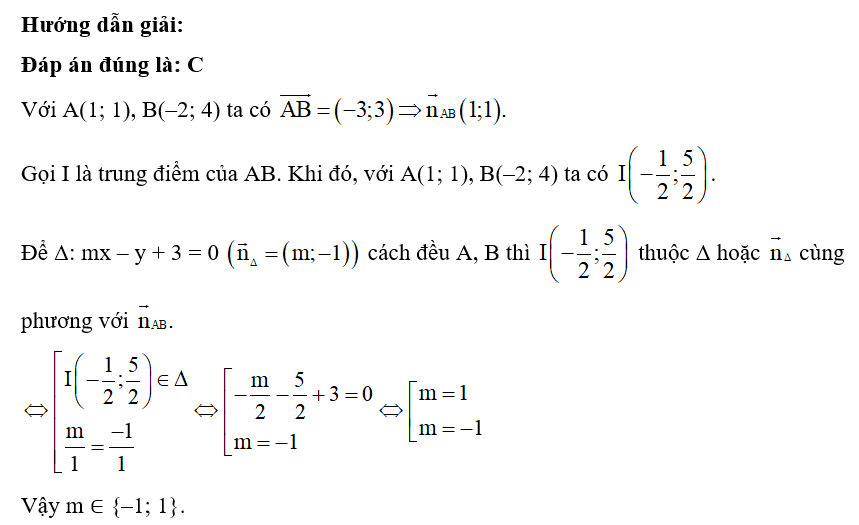10 câu hỏi trắc nghiệm thuộc Dạng 5. Phương trình đường thẳng liên quan đến khoảng cách

Câu 1:

Cho hai điểm A(3; 1), B(4; 0). Đường thẳng không đi qua A, B có phương trình nào sau đây cách đều A và B?

A. –2x + 2y – 3 = 0;

B. x – y – 3 = 0;

C. x + 2y – 3 = 0;

D. 2x + y – 3 = 0.

Xem đáp án

Cho hai điểm A(3; 1), B(4; 0). Đường thẳng không đi qua A, B có phương trình nào sau đây cách đều A và B? (ảnh 1)

Câu 2:

Trong mặt phẳng tọa độ Oxy, phương trình đường thẳng đi qua A(–1; 2) và cách B(3; 5) một khoảng bằng 3 là

A. Δ₁: y + 2 = 0 và Δ₂: 24x – 7y + 38 = 0;

B. Δ₁: y – 2 = 0 và Δ₂: 24x + 7y + 38 = 0;

C. Δ₁: y – 2 = 0 và Δ₂: 24x – 7y + 38 = 0;

D. Δ₁: y + 2 = 0 và Δ₂: 24x + 7y + 38 = 0.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C

Gọi phương trình đường thẳng Δ là ax + by + c = 0 (với a² + b² ≠ 0).

Điểm A(–1; 2) thuộc vào đường thẳng Δ tức là –a + 2b + c = 0 suy ra c = a – 2b (1)

Khoảng cách từ B(3; 5) đến đường thẳng Δ bằng 3 nên ta có:

$\frac{|3 a + 5 b + c|}{\sqrt{a^{2} + b^{2}}} = 3 \Leftrightarrow |3 a + 5 b + c| = 3 \sqrt{a^{2} + b^{2}} (2)$

Thay (1) vào (2), ta có:

$|4 a + 3 b| = 3 \sqrt{a^{2} + b^{2}} \Leftrightarrow 16 a^{2} + 24 a b + 9 b^{2} = 9 a^{2} + 9 b^{2}$

$\Leftrightarrow 7 a^{2} + 24 a b = 0 \Leftrightarrow [\begin{array}{l} a = 0 \\ 7 a + 24 b = 0 \end{array}$ .

Với a = 0, chọn b = 1 suy ra c = –2. Vậy đường thẳng Δ₁: y – 2 = 0.

Với 7a + 24b = 0, chọn b = –7 suy ra a = 24, c = 38. Vậy phương trình đường thẳng Δ₂: 24x – 7y + 38 = 0.

Câu 3:

Trong mặt phẳng tọa độ Oxy, phương trình đường thẳng d vuông góc với đường thẳng Δ: 2x + y – 1 = 0 và cách điểm M(3; – 2) một khoảng bằng $\sqrt{5}$ là

A. d₁: x – 2y – 12 = 0 và d₂: x – 2y – 2 = 0;

B. d₁: x – 2y – 12 = 0 và d₂: x – 2y + 2 = 0;

C. d₁: x – 2y + 12 = 0 và d₂: x – 2y – 2 = 0;

D. d₁: x – 2y + 12 = 0 và d₂: x – 2y + 2 = 0.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A

Đường thẳng Δ: 2x + y – 1 = 0 có một vectơ pháp tuyến ${\vec{n}}_{Δ} = (2; 1)$

Đường thẳng d vuông góc với đường thẳng Δ nên d nhận ${\vec{n}}_{d} = (1; - 2)$ làm một vectơ pháp tuyến. Khi đó giả sử đường thẳng d có phương trình dạng: x – 2y + c = 0.

Vì d cách điểm M(3; – 2) một khoảng bằng $\sqrt{5}$ nên ta có:

$d (M, d) = \sqrt{5} \Leftrightarrow \frac{|3 - 2 \cdot (- 2) + c|}{\sqrt{1^{2} + {(- 2)}^{2}}} = \sqrt{5} \Leftrightarrow |c + 7| = 5 \Leftrightarrow [\begin{array}{l} c = - 12 \\ c = - 2 \end{array}$ .

Vậy có hai đường thẳng d thỏa mãn yêu cầu bài toán là: d₁: x – 2y – 12 = 0 và d₂: x – 2y – 2 = 0.

Câu 4:

Trong mặt phẳng tọa độ Oxy, phương trình đường thẳng d song song với d’: 3x + 4y – 1 = 0 và cách d’ một khoảng bằng 2 là

A. d: 3x + 4y – 9 = 0 hoặc d: 3x + 4y + 11 = 0;

B. d: 3x + 4y + 9 = 0 hoặc d: 3x + 4y – 11 = 0;

C. d: 3x + 4y + 3 = 0 hoặc d: 3x + 4y – 17 = 0;

D. d: 3x + 4y – 3 = 0 hoặc d: 3x + 4y + 17 = 0.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B

Đường thẳng d song song với đường thẳng d’ nên phương trình đường thẳng d’ có dạng 3x + 4y + c = 0.

Lấy điểm M(–1; 1) thuộc vào d’ nên ta có:

$d (d, d^{'}) = d (M, d^{'}) = 2 \Leftrightarrow \frac{|- 3 + 4 + c|}{5} = 2 \Leftrightarrow |c + 1| = 10 \Leftrightarrow [\begin{array}{l} c = 9 \\ c = - 11 \end{array}$ .

Với c = 9 ta có d : 3x + 4y + 9 = 0.

Với c = –11 ta có d: 3x + 4y – 11 = 0.

Câu 5:

Trong mặt phẳng với hệ tọa độ Oxy, cho ba điểm A(0; 1), B(12; 5) và C(–3; 0). Đường thẳng có phương trình nào sau đây cách đều ba điểm A, B và C?

A. x – 3y + 4 = 0;

B. –x + y + 10 = 0;

C. x + y = 0;

D. 5x – y + 1 = 0.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A

Ta có $\vec{A B} = (12; 4)$ và $\vec{A C} = (- 3; - 1) = - 4 \vec{A B}$ nên hai vectơ này cùng phương.

Do đó ba điểm A, B, C thẳng hàng nên đường thẳng d cách đều A, B, C là đường thẳng song song hoặc trùng với AB.

Ta thấy trong 4 phương án, không có đường thẳng nào đi qua A nên ta loại trường hợp d trùng AB. Khi đó đường thẳng d // AB.

Ta thấy đường thẳng x – 3y + 4 = 0 có một vectơ pháp tuyến là $\vec{n} = (1; - 3)$ nên nhận $\vec{A B} = (12; 4)$ làm một vectơ chỉ phương. Do đó đường thẳng này song song với AB.

Vậy ta chọn phương án A.

Câu 6:

Trong mặt phẳng tọa độ Oxy, cho hai điểm A(1; 1), B(–2; 4) và đường thẳng Δ: mx – y + 3 = 0. Giá trị của tham số m để Δ cách đều hai điểm A, B là

A. m ∈ {1; –2};

B. m ∈ {–1; 2};

C. m ∈ {–1; 1};

D. m ∈ {–2; 2}.

Xem đáp án

Trong mặt phẳng tọa độ Oxy, cho hai điểm A(1; 1), B(–2; 4) và đường thẳng (ảnh 1)

Câu 7:

Trong mặt phẳng tọa độ Oxy, tập hợp các điểm cách đường thẳng Δ: 3x – 4y + 2 = 0 một khoảng bằng 2 là hai đường thẳng có phương trình nào sau đây?

A. 3x – 4y + 8 = 0; 3x – 4y + 12 = 0;

B. 3x – 4y – 8 = 0; 3x – 4y + 12 = 0;

C. 3x – 4y – 8 = 0; 3x – 4y – 12 = 0;

D. 3x – 4y + 8 = 0; 3x – 4y – 12 = 0.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B

Giả sử M(x; y) là điểm cách đường thẳng Δ: 3x – 4y + 2 = 0 một khoảng bằng 2.

Ta có:

$d (M, Δ) = 2 \Leftrightarrow \frac{|3 x - 4 y + 2|}{5} = 2 \Leftrightarrow |3 x - 4 y + 2| = 10 \Leftrightarrow [\begin{array}{l} 3 x - 4 y + 12 = 0 \\ 3 x - 4 y - 8 = 0 \end{array}$ .

Vậy tập hợp điểm M là hai đường thẳng 3x – 4y – 8 = 0; 3x – 4y + 12 = 0.

Câu 8:

Trong mặt phẳng tọa độ Oxy, cho đường thẳng Δ: x + (m – 1)y + m = 0 (m là tham số bất kỳ) và điểm A(5; 1). Khoảng cách lớn nhất từ điểm A đến Δ bằng

A. $\sqrt{10}$ ;

B. $2 \sqrt{10}$ ;

C. $3 \sqrt{10}$ ;

D.

4 \sqrt{10}

.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B

Gọi H(x₀; y₀) là điểm cố định mà đường thẳng Δ luôn đi qua.

Khi đó x₀ + (m – 1)y₀ + m = 0 với mọi m

⇔ (y₀ + 1)m + x₀ – y₀ = 0 với mọi m

$\Leftrightarrow \{\begin{cases} y_{0} + 1 = 0 \\ x_{0} - y_{0} = 0 \end{cases} \Leftrightarrow \{\begin{cases} y_{0} = - 1 \\ x_{0} = y_{0} \end{cases} \Leftrightarrow \{\begin{cases} x_{0} = - 1 \\ y_{0} = - 1 \end{cases}$

Suy ra Δ luôn đi qua điểm cố định H(–1; –1).

Với A(5; 1) và H(–1; –1) ta có $\vec{A H} = (- 6; - 2)$ nên $A H = \sqrt{{(- 6)}^{2} + {(- 2)}^{2}} = 2 \sqrt{10} .$

Gọi M là hình chiếu của A trên Δ, ta có d(A, ∆) = AM ≤ AH.

Giá trị lớn nhất của d(A, Δ) = AH khi M ≡ H, suy ra maxd(A, Δ) = AH = $2 \sqrt{10}$ .

Câu 9:

Trong mặt phẳng với hệ tọa độ Oxy, cho hai đường thẳng d₁: 5x + 3y – 3 = 0 và d₂: 5x + 3y + 7 = 0 song song nhau. Đường thẳng vừa song song và cách đều với d₁, d₂ là:

A. 5x + 3y – 2 = 0;

B. 5x + 3y + 4 = 0;

C. 5x + 3y + 2 = 0;

D. 5x + 3y – 4 = 0.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C

Gọi M(x; y) là điểm nằm trên đường thẳng song song và cách đều với d₁, d₂.

Ta có $d (M (x; y), d_{1}) = d (M (x; y), d_{2}) \Leftrightarrow \frac{|5 x + 3 y - 3|}{\sqrt{5^{2} + 3^{2}}} = \frac{|5 x + 3 y + 7|}{\sqrt{5^{2} + 3^{2}}}$

$\Leftrightarrow [\begin{array}{l} 5 x + 3 y - 3 = 5 x + 3 y + 7 (v ô l í) \\ 5 x + 3 y - 3 = - 5 x - 3 y - 7 \end{array}$

$\Leftrightarrow 5 x + 3 y + 2 = 0.$

Câu 10:

Trên mặt phẳng tọa độ Oxy, cho các điểm A(1; −1) và B(3; 4). Gọi (d) là một đường thẳng bất kì luôn đi qua B. Khi khoảng cách từ A đến đường thẳng (d) đạt giá trị lớn nhất, đường thẳng (d) có phương trình nào dưới đây?

A. x – y + 1 = 0;

B. 3x + 4y = 25;

C. 5x – 2y – 7 = 0;

D. 2x + 5y – 26 = 0.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D

Gọi H là hình chiếu của điểm A lên đường thẳng (d).

Khi đó ta có: $d (A, (d)) = A H \leq A B = \sqrt{{(3 - 1)}^{2} + {(4 + 1)}^{2}} = \sqrt{29}$ .

Do đó khoảng cách từ A đến đường thẳng (d) đạt giá trị lớn nhất bằng $\sqrt{29}$ khi H ≡ B hay (d) ⊥ AB tại B.

Vì vậy (d) đi qua B và nhận $\vec{A B} = (2; 5)$ làm vectơ pháp tuyến.

Do đó phương trình của đường thẳng (d) là 2(x – 3) + 5(y – 4) = 0 hay 2x + 5y – 26 = 0.

Trắc nghiệm Toán 10 Bài 20. Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách có đáp án

Dạng 5. Phương trình đường thẳng liên quan đến khoảng cách

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương