10 câu hỏi trắc nghiệm thuộc Dạng 2. Xác định góc giữa hai đường thẳng cho trước

Câu 1:

Trong mặt phẳng tọa độ Oxy, góc tạo bởi hai đường thẳng d₁: 2x – y – 10 = 0 và d₂: x – 3y + 9 = 0 bằng

A. 30°;

B. 45°;

C. 60°;

D. 135°.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B

Ta có:

Đường thẳng d₁: 2x – y – 10 = 0 có vectơ pháp tuyến ${\vec{n}}_{1} (2; - 1)$ .

Đường thẳng d₂: x – 3y + 9 = 0 có vectơ pháp tuyến ${\vec{n}}_{2} (1; - 3)$ .

Gọi α là góc giữa hai đường thẳng. Khi đó:

$\cos α = |\cos ({\vec{n}}_{1}, {\vec{n}}_{2})| = \frac{|{\vec{n}}_{1} \cdot {\vec{n}}_{2}|}{|{\vec{n}}_{1}| . |{\vec{n}}_{2}|} = \frac{|2 \cdot 1 + (- 1) \cdot (- 3)|}{\sqrt{2^{2} + {(- 1)}^{2}} \cdot \sqrt{1^{2} + {(- 3)}^{2}}} = \frac{5}{\sqrt{5} \cdot \sqrt{10}} = \frac{1}{\sqrt{2}} .$

Do đó α = 45°.

Vậy góc giữa hai đường thẳng d₁ và d₂ là 45°.

Câu 2:

Trong mặt phẳng tọa độ Oxy, góc tạo bởi giữa hai đường thẳng d₁: $\{\begin{cases} x = 3 + 2 t \\ y = 1 + 2 \sqrt{3} t \end{cases}$ và d₂: $\{\begin{cases} x = - 1 \\ y = t \end{cases}$ bằng

A. 30°;

B. 45°;

C. 60°;

D. 90°.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A

Đường thẳng d₁ có vectơ chỉ phương ${\vec{u}}_{1} (2; 2 \sqrt{3})$ .

Đường thẳng d₂ có vectơ chỉ phương ${\vec{u}}_{2} (0; 1)$ .

Gọi α là góc giữa hai đường thẳng. Khi đó:

$\cos α = |\cos ({\vec{u}}_{1}, {\vec{u}}_{2})| = \frac{|{\vec{u}}_{1} . {\vec{u}}_{2}|}{|{\vec{u}}_{1}| \cdot |{\vec{u}}_{2}|} = \frac{|2 \cdot 0 + 2 \sqrt{3} \cdot 1|}{\sqrt{2^{2} + {(2 \sqrt{3})}^{2}} \cdot \sqrt{0^{2} + 1^{2}}} = \frac{2 \sqrt{3}}{4} = \frac{\sqrt{3}}{2} .$

Do đó α = 30°.

Vậy góc giữa hai đường thẳng d₁ và d₂ là 30°.

Câu 3:

Trong mặt phẳng tọa độ Oxy, góc tạo bởi giữa hai đường thẳng d₁: 6x – 5y + 15 = 0 và d₂: $\{\begin{cases} x = 10 - 6 t \\ y = 1 + 5 t \end{cases}$ bằng

A. 30°;

B. 45°;

C. 60°;

D. 90°.

Xem đáp án

Trong mặt phẳng tọa độ Oxy, góc tạo bởi giữa hai đường thẳng d1: 6x – 5y + 15 = 0 (ảnh 1)

Câu 4:

Trong mặt phẳng tọa độ Oxy, cho đường thẳng d₁: x + 2y – 7 = 0 và d₂: $\{\begin{cases} x = - 1 + 2 t \\ y = 3 + t \end{cases} .$ Cosin của góc tạo bởi giữa hai đường thẳng d₁ và d₂ là

A. $- \frac{3}{5}$ ;

B. $\frac{2}{\sqrt{5}}$ ;

C. $\frac{3}{5}$ ;

D.

\frac{3}{\sqrt{5}}

.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C

Đường thẳng d₁ có vectơ pháp tuyến ${\vec{n}}_{1} (1; 2)$ .

Đường thẳng d₂ có vectơ chỉ phương ${\vec{u}}_{2} = (2; 1)$ nên có một vectơ pháp tuyến ${\vec{n}}_{2} (1; - 2) .$

Gọi α là góc giữa hai đường thẳng. Khi đó:

$\cos α = |\cos ({\vec{n}}_{1}, {\vec{n}}_{2})| = \frac{|{\vec{n}}_{1} \cdot {\vec{n}}_{2}|}{|{\vec{n}}_{1}| \cdot |{\vec{n}}_{2}|} = \frac{|1 \cdot 1 + 2 \cdot (- 2)|}{\sqrt{1^{2} + 2^{2}} . \sqrt{1^{2} + {(- 2)}^{2}}} = \frac{3}{5}$ .

Câu 5:

Trong mặt phẳng tọa độ Oxy, cho đường thẳng d₁: x + 2y – 2 = 0 và d₂: x – y = 0. Cosin của góc tạo bởi giữa hai đường thẳng đã cho là

A. $\frac{\sqrt{10}}{10}$ ;

B. $\frac{\sqrt{2}}{3}$ ;

C. $\frac{\sqrt{3}}{3}$

D.

\sqrt{3}

.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A

Đường thẳng d₁: x + 2y – 2 = 0 có vectơ pháp tuyến ${\vec{n}}_{1} (1; 2)$ .

Đường thẳng d₂: x – y = 0 có vectơ pháp tuyến ${\vec{n}}_{2} (1; - 1)$ .

Gọi α là góc giữa hai đường thẳng. Khi đó:

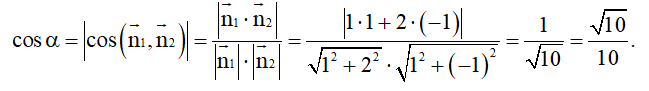
Trong mặt phẳng tọa độ Oxy, cho đường thẳng d1: x + 2y – 2 = 0 và d2: x – y = 0. (ảnh 1)

Câu 6:

Trong mặt phẳng tọa độ Oxy, góc giữa hai đường thẳng Δ₁: x – 2y + 15 = 0 và Δ₂: $\{\begin{cases} x = 2 - t \\ y = 4 + 2 t \end{cases}$ bằng

A. 5°;

B. 60°;

C. 0°;

D. 90°.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D

Đường thẳng Δ₁ có vectơ pháp tuyến ${\vec{n}}_{1} (1; - 2)$ , nên có một vectơ chỉ phương là ${\vec{u}}_{1} (2; 1)$ .

Đường thẳng Δ₂ có vectơ chỉ phương là ${\vec{u}}_{2} (- 1; 2)$ .

Ta có: ${\vec{u}}_{1} \cdot {\vec{u}}_{2} = 2 \cdot (- 1) + 1 \cdot 2 = 0$ suy ra góc giữa hai đường thẳng Δ₁ và Δ₂ là 90°.

Câu 7:

Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng d₁: 3x + 4y + 1 = 0 và d₂: $\{\begin{cases} x = 15 + 12 t \\ y = 1 + 5 t \end{cases}$ . Cosin của góc tạo bởi giữa hai đường thẳng đã cho là

A. $\frac{55}{65}$ ;

B. $- \frac{33}{65}$ ;

C. $\frac{6}{65}$ ;

D.

\frac{33}{65}

.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D

Đường thẳng d₁: 3x + 4y + 1 = 0 có vectơ pháp tuyến ${\vec{n}}_{1} (3; 4)$ .

Đường thẳng d₂: $\{\begin{cases} x = 15 + 12 t \\ y = 1 + 5 t \end{cases}$ có vectơ chỉ phương là ${\vec{u}}_{2} (12; 5)$ nên có một pháp tuyến ${\vec{n}}_{2} (5; - 12)$ .

Gọi α là góc giữa hai đường thẳng. Khi đó:

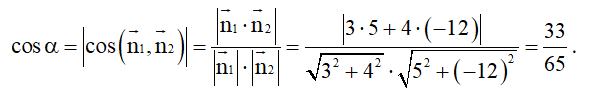
Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng d1: 3x + 4y + 1 = 0 và d2: x= 15+ 12t và y= 1+ 5t (ảnh 1)

.

Câu 8:

Trong mặt phẳng tọa độ Oxy, cho đường thẳng d₁: 10x + 5y – 1 = 0 và d₂: $\{\begin{cases} x = 2 + t \\ y = 1 - t \end{cases} .$ Cosin của góc tạo bởi giữa hai đường thẳng đã cho là

A. $\frac{3 \sqrt{10}}{10}$ ;

B. $\frac{3}{5}$ ;

C. $\frac{\sqrt{10}}{10}$ ;

D.

\frac{3}{10}

.

Xem đáp án

Trong mặt phẳng tọa độ Oxy, cho đường thẳng d1: 10x + 5y – 1 = 0 và d2: x= 2+t và y= 1- t .Cosin (ảnh 1)

Câu 9:

Trong mặt phẳng tọa độ Oxy, đường thẳng d₁: (3 + m)x – (m – 1)y = 0 tạo với đường thẳng d₂: (m – 2)x + (m + 1)y – 20 = 0 một góc 90°. Giá trị của m là

A. m = 5;

B. m = –5;

C. m = 6;

D. m = 4.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A

Đường thẳng d₁: (3 + m)x – (m – 1)y = 0 có vectơ pháp tuyến ${\vec{n}}_{1} (3 + m; - m + 1)$ .

Đường thẳng d₂: (m – 2)x + (m + 1)y – 20 = 0 có vectơ pháp tuyến ${\vec{n}}_{2} (m - 2; m + 1)$ .

Góc giữa hai đường thẳng bằng 90° nên ${\vec{n}}_{1} \cdot {\vec{n}}_{2} = 0$ , tức là:

(3 + m)(m – 2) + (1 – m)(m + 1) = 0

⇔ m² + m – 6 + 1 – m² = 0

⇔ m = 5

Vậy m = 5 là giá trị cần tìm.

Câu 10:

Trong mặt phẳng tọa độ Oxy, đường thẳng d₁: 2mx + (m – 3)y – 1 = 0 tạo với đường thẳng d₂: (m – 1)x + (–2m + 2)y – 2 = 0 (với m ≠ 1) một góc 45°. Giá trị m nào sau đây là một trong những giá trị thỏa mãn yêu cầu đề bài?

A. $m = \frac{9}{5}$ ;

B. m = 1;

C. m = 5;

D. m = 0.

Xem đáp án

Trắc nghiệm Toán 10 Bài 20. Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách có đáp án

Dạng 2. Xác định góc giữa hai đường thẳng cho trước

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương