10 câu hỏi trắc nghiệm thuộc Dạng 4. Khoảng cách từ điểm đến đường thẳng

Câu 1:

Trong mặt phẳng tọa độ Oxy, khoảng cách từ điểm A(1; 1) đến đường thẳng Δ: 5x – 12y – 6 = 0 là

A. 13

B. –13;

C. –1;

D. 1.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D

Khoảng cách từ điểm A(1; 1) đến đường thẳng Δ: 5x – 12y – 6 = 0 là $d (A, Δ) = \frac{|5.1 - 12.1 - 6|}{\sqrt{5^{2} + {(- 12)}^{2}}} = 1$ .

Câu 2:

Trong mặt phẳng tọa độ Oxy, khoảng cách từ giao điểm của hai đường thẳng x – 3y + 4 = 0 và 2x + 3y – 1 = 0 đến đường thẳng d: 3x + y + 4 = 0 bằng

A. $2 \sqrt{10}$ ;

B. $\frac{3 \sqrt{10}}{5}$ ;

C. $\frac{\sqrt{10}}{5}$ ;

D. 2.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C

Giao điểm của hai đường thẳng x – 3y + 4 = 0 và 2x + 3y – 1 = 0 là nghiệm của hệ phương trình: $\{\begin{cases} x - 3 y + 4 = 0 \\ 2 x + 3 y - 1 = 0 \end{cases} \Leftrightarrow \{\begin{cases} x = - 1 \\ y = 1 \end{cases}$ .

Suy ra tọa độ giao điểm của hai đường thẳng là A(–1; 1).

Khoảng cách từ điểm A đến đường thẳng d: 3x + y + 4 = 0 bằng $d (A, Δ) = \frac{|- 3 + 1 + 4|}{\sqrt{3^{2} + 1^{2}}} = \frac{2}{\sqrt{10}} = \frac{\sqrt{10}}{5}$ .

Câu 3:

Trong mặt phẳng tọa độ Oxy, khoảng cách từ điểm M(2; 0) đến đường thẳng Δ: $\{\begin{cases} x = 1 + 3 t \\ y = 2 + 4 t \end{cases}$ bằng

A. 2;

B. $\frac{2}{5}$ ;

C. $\frac{10}{\sqrt{5}}$ ;

D.

v \frac{\sqrt{5}}{2}

.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A

Đường thẳng Δ: $\{\begin{cases} x = 1 + 3 t \\ y = 2 + 4 t \end{cases}$ viết dưới dạng phương trình tổng quát là:

$\frac{x - 1}{3} = \frac{y - 2}{4} \Leftrightarrow 4 (x - 1) = 3 (y - 2)$

⇔ 4x – 3y + 2 = 0.

Khoảng cách từ điểm M(2; 0) đến đường thẳng Δ là $d (M, Δ) = \frac{|4 \cdot 2 - 3 \cdot 0 + 2|}{\sqrt{4^{2} + {(- 3)}^{2}}} = 2$ .

Câu 4:

Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có A(1; 2), B(0; 3) và C(4; 0). Chiều cao của tam giác kẻ từ đỉnh A bằng

A. $\frac{1}{5};$

B. $\frac{1}{25};$

C. $\frac{3}{5};$

D. 3.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

Với B(0; 3) và C(4; 0) ta có $\vec{B C} = (4; - 3)$

Khi đó đường thẳng BC đi qua B(0; 3) và nhận $\vec{n} (3; 4)$ làm một vectơ pháp tuyến nên có phương trình là: 3(x – 0) + 4(y – 3) = 0 hay 3x + 4y – 12 = 0.

Khi đó khoảng cách từ A(1; 2) đến đường thẳng BC chính là chiều cao kẻ từ A của tam giác ABC, và bằng

$d (A, B C) = \frac{|3 \cdot 1 + 4 \cdot 2 - 12|}{\sqrt{3^{2} + 4^{2}}} = \frac{1}{5} .$

Câu 5:

Khoảng cách nhỏ nhất từ điểm M(15; 1) đến một điểm bất kì thuộc đường thẳng $Δ : \{\begin{cases} x = 2 + 3 t \\ y = t \end{cases}$ bằng:

A. $\sqrt{10};$

B. $\frac{1}{\sqrt{10}};$

C. $\frac{16}{\sqrt{5}};$

D.

\sqrt{5};

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

Phương trình đường thẳng $Δ : \{\begin{cases} x = 2 + 3 t \\ y = t \end{cases}$ được viết thành: $\frac{x - 2}{3} = \frac{y}{1}$ hay x – 3y – 2 = 0.

Khoảng cách nhỏ nhất từ điểm M(15; 1) đến một điểm bất kì thuộc đường thẳng ∆ chính là khoảng cách từ điểm M đến ∆, và bằng:

$d (M, Δ) = \frac{|15 - 3 \cdot 1 - 2|}{\sqrt{1^{2} + {(- 3)}^{2}}} = \frac{10}{\sqrt{10}} = \sqrt{10} .$

Câu 6:

Giá trị của tham số m để khoảng cách từ điểm A(−1; 2) đến đường thẳng Δ: mx + y – m + 4 = 0 bằng $2 \sqrt{5}$ là

A. m = 2;

B. m = –2 hoặc $m = \frac{1}{2}$ ;

C. $m = - \frac{1}{2}$ ;

D. Không có giá trị của m.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B

Khoảng cách từ điểm A đến đường thẳng Δ bằng:

$d (A, Δ) = \frac{|m \cdot (- 1) + 2 - m + 4|}{\sqrt{m^{2} + 1^{2}}} = 2 \sqrt{5}$

$\Leftrightarrow |m - 3| = \sqrt{5} \cdot \sqrt{m^{2} + 1} \Leftrightarrow m^{2} - 6 m + 9 = 5 (m^{2} + 1)$

$\Leftrightarrow 4 m^{2} + 6 m - 4 = 0 \Leftrightarrow [\begin{array}{l} m = - 2 \\ m = \frac{1}{2} \end{array}$

Vậy ta chọn phương án B.

Câu 7:

Đường tròn (C) có tâm là gốc tọa độ O(0; 0) và tiếp xúc với đường thẳng ∆: 8x + 6y + 100 = 0. Bán kính R của đường tròn (C) bằng

A. R = 4;

B. R = 6;

C. R = 8;

D. R = 10.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D

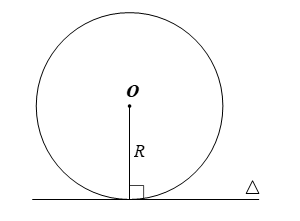
Đường tròn (C) có tâm là gốc tọa độ O(0; 0) và tiếp xúc với đường thẳng ∆: 8x + 6y + 100 = 0. Bán kính R của đường tròn (C) bằng (ảnh 1)

Vì (C) tiếp xúc với ∆ nên khoảng cách từ O đến đường thẳng ∆ chính là bán kính của đường tròn, và bằng:

$R = d (O, Δ) = \frac{|8 \cdot 0 + 6 \cdot 0 + 100|}{\sqrt{8^{2} + 6^{2}}} = \frac{100}{10} = 10.$

Câu 8:

Khoảng cách từ điểm M(0; 3) đến đường thẳng ∆: xcosα + ysinα + 3(2 – sinα) = 0 bằn

A. $\sqrt{6};$

B. 6

C. 3sinα;

D. $\frac{3}{\cos α + \sin α} .$

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B

Ta có $d (M, Δ) = \frac{|0 \cdot cos α + 3 \sin α + 3 (2 - \sin α)|}{\sqrt{\cos^{2} α + \sin^{2} α}} = \frac{|6|}{\sqrt{1}} = 6.$

Câu 9:

Khoảng cách giữa hai đường thẳng song song d₁: 6x – 8y – 101 = 0 và d₂: 3x – 4y = 0 bằng:

A. 10,1;

B. 1,01;

C. 101;

D.

\sqrt{101}

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A

Ta có d₁ và d₂ song song với nhau nên ta chọn A(4; 3) ∈ d₂.

Khi đó $d (d_{1}, d_{2}) = d (A, d_{1}) = \frac{|6 \cdot 4 - 8 \cdot 3 - 101|}{\sqrt{6^{2} + {(- 8)}^{2}}} = \frac{101}{10} = 10, 1.$

Câu 10:

Khoảng cách giữa hai đường thẳng d: 7x + y – 3 = 0 và $Δ : \{\begin{cases} x = - 2 + t \\ y = 2 - 7 t \end{cases}$ bằng

A. $\frac{3 \sqrt{2}}{2}$ ;

B. 15;

C. 9;

D.

\frac{9}{\sqrt{50}}

.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A

Đường thẳng d có một vectơ pháp tuyến là ${\vec{n}}_{d} (7; 1)$ nên có một vectơ chỉ phương là ${\vec{u}}_{d} (1; - 7) .$

Đường thẳng ∆ có một vectơ chỉ phương là ${\vec{u}}_{Δ} (1; - 7) .$

Do đó hai đường thẳng d và ∆ song song với nhau.

Lấy A(–2; 2) ∈ ∆. Khi đó $d (d, Δ) = d (A, d) = \frac{|7 \cdot (- 2) + 2 - 3|}{\sqrt{7^{2} + 1^{2}}} = \frac{15}{\sqrt{50}} = \frac{3 \sqrt{2}}{2} .$

Trắc nghiệm Toán 10 Bài 20. Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách có đáp án

Dạng 4. Khoảng cách từ điểm đến đường thẳng

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương