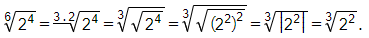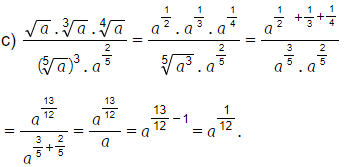Giải SGK Toán 11 (Chân trời sáng tạo) Bài 1: Phép tính lũy thừa

Giải Toán 11 Bài 1: Phép tính lũy thừa

Hoạt động khởi động trang 6 Toán 11 Tập 2: Trong khoa học, người ta thường dùng lũy thừa để ghi các số, có thể rất lớn hoặc rất bé. Chẳng hạn, bảng dưới đây cho một số ví dụ về cách ghi độ dài.

Cách ghi như vậy có tiện ích gì? Từ các lũy thừa quen thuộc ở ba dòng đầu, hãy dự đoán quy tắc viết lũy thừa ở ba dòng cuối.

Lời giải:

Các ghi bằng lũy thừa giúp cho việc viết và đọc số (đặc biệt với các số rất lớn hoặc rất bé) ngắn gọn.

Nhận thấy: ${10}^{-3}=\mathrm{0,001}=\frac{1}{1000}=\frac{1}{{10}^3}$.

Tương tự, ${10}^{-6}=\frac{1}{{10}^6};{10}^{-9}=\frac{1}{{10}^9}.$.

Từ đó, dự đoán: ${10}^{-n}=\frac{1}{{10}^n}$ (nghịch đảo của 10ⁿ) với n là số tự nhiên khác 0.

1. Lũy thừa với số mũ nguyên

Hoạt động khám phá 1 trang 6 Toán 11 Tập 2: Cho biết dãy số (a_n) được xác định theo một quy luật nào đó và bốn số hạng đầu tiên của nó được cho như ở bảng dưới đây:

a) Tìm quy luật của dãy số và tìm ba số hạng tiếp theo của nó.

b) Nếu viết các số hạng của dãy số dưới dạng lũy thừa, thì bốn số hạng đầu tiên có thể viết thành $2^4;2^3;2^2;2^1.$ Dự đoán cách viết dưới dạng lũy thừa của ba số hạng tiếp theo của dãy số và giải thích.

Lời giải:

a) Quy luật: Mỗi số hạng (kể từ số hạng thứ hai) bằng số hạng đứng trước nó chia cho 2.

Vậy ba số hạng tiếp theo là: $a_5=1;a_6=\frac{1}{2};a_7=\frac{1}{4}.$

b) Các số hạng của dãy số có dạng 2ⁿ, với số mũ của số liền sau ít hơn số mũ của số liền trước 1 đơn vị.

Vậy ta có thể viết ba số hạng tiếp theo là: a₅=2⁰;a₆=2⁻¹;a₇=2⁻².

Thực hành 1 trang 7 Toán 11 Tập 2: Tính giá trị các biểu thức sau:

a) ${\left(-5\right)}^{-1}$;

b) $2^0\cdot {\left(\frac{1}{2}\right)}^{-5}$;

c) $6^{-2}\cdot {\left(\frac{1}{3}\right)}^{-3}:2^{-2}$.

Lời giải:

a) ${\left(-5\right)}^{-1}=\frac{1}{{\left(-5\right)}^1}=\frac{1}{-5}=-\frac{1}{5}$;

b) $2^0\cdot {\left(\frac{1}{2}\right)}^{-5}=2^0\cdot \frac{1}{{\left(\frac{1}{2}\right)}^5}=1\cdot \frac{1}{\frac{1}{32}}=32$;

c) $6^{-2}\cdot {\left(\frac{1}{3}\right)}^{-3}:2^{-2}=\frac{1}{6^2}\cdot \frac{1}{{\left(\frac{1}{3}\right)}^3}:\frac{1}{2^2}$

$=\frac{1}{36}\cdot \frac{1}{\frac{1}{27}}:\frac{1}{4}=\frac{1}{36}\cdot 27\cdot 4=3.$

Vận dụng 1 trang 7 Toán 11 Tập 2: Trong khoa học, người ta thường phải ghi các số rất lớn hoặc rất bé. Để tránh phải viết và đếm quá nhiều chữ số 0 , người ta quy ước cách ghi các số dưới dạng A.10^m, trong đó 1 ≤ A ≤ 10 và m là số nguyên.

Khi một số được ghi dưới dạng này, ta nói nó được ghi dưới dạng ki hiệu khoa học.

Chẳng hạn, khoảng cách 149 600 000 km từ Trái Đất đến Mặt Trời được ghi dưới dạng kí hiệu khoa học là $\mathrm{1,496}.{10}^8\text{ km}$.

Ghi các đại lượng sau dưới dạng kí hiệu khoa học:

a) Vận tốc ánh sáng trong chân không là 299 790 000 m/s;

b) Khối lượng nguyên tử của oxygen là

$\mathrm{0,000}00000000000000000000002657\text{ kg}$.

Lời giải:

a) Ta có 299 790 000 = 2,9979.10⁸.

Do đó, vận tốc ánh sáng trong chân không là 2,9979.10⁸m/s;

b) Ta có $\mathrm{0,000}00000000000000000000002657$= 2,657.10⁻²⁶.

Do đó, khối lượng nguyên tử của oxygen là 2,657.10⁻²⁶kg.

2. Căn bậc n

Hoạt động khám phá 2 trang 7 Toán 11 Tập 2: Một thùng gỗ hình lập phương có độ dài cạnh a (dm). Kí hiệu S và V lần lượt là diện tích một mặt và thể tích của thùng gỗ này.

a) Tính S và V khi a = 1 dm và khi a = 3 dm .

b) a bằng bao nhiêu để S = 25 dm² ?

c) a bằng bao nhiêu để V = 64 dm³ ?

Lời giải:

a) Khi a = 1 dm , ta có:

S = a² = 1² = 1 (dm²); V = a³ = 1³ = 1 (dm³)

Khi a = 3 dm , ta có:

S = a² = 3² = 9 (dm²); V = a³ = 3³ = 27 (dm³) .

Thực hành 2 trang 9 Toán 11 Tập 2: Tính giá trị các biểu thức sau:

a) $\sqrt[4]{\frac{1}{16}}$;

b) ${\left(\sqrt[6]{8}\right)}^2$;

c) $\sqrt[4]{3}\cdot \sqrt[4]{27}$.

Lời giải:

3. Lũy thừa với số mũ hữu tỉ

Hoạt động khám phá 3 trang 9 Toán 11 Tập 2: a) Hai biểu thức $\sqrt[6]{2^4}$ và $\sqrt[3]{2^2}$ có giá trị bằng nhau không? Giải thích.

b) Chỉ ra ít nhất hai biểu thức khác nhau có giá trị bằng $\sqrt[3]{2^2}$.

Lời giải:

a) Ta có 

Vậy $\sqrt[6]{2^4}=\sqrt[3]{2^2}$.

b) Ta có $\sqrt[3]{2^2}=\sqrt[9]{2^6}=\sqrt[12]{2^8}.$

Vậy có ít nhất hai biểu thức khác nhau có giá trị bằng $\sqrt[3]{2^2}$ là $\sqrt[9]{2^6};\sqrt[12]{2^8}.$

Thực hành 3 trang 10 Toán 11 Tập 2: Tính giá trị biểu thức sau:

a) ${25}^{\frac{1}{2}}$;

b) ${\left(\frac{36}{49}\right)}^{-\frac{1}{2}}$;

c) ${100}^{\mathrm{1,5}}.$

Lời giải:

a) ${25}^{\frac{1}{2}}=\sqrt{25}=\sqrt{5^2}=5;$

b) ${\left(\frac{36}{49}\right)}^{-\frac{1}{2}}=\frac{1}{{\left(\frac{36}{49}\right)}^{\frac{1}{2}}}=\frac{1}{\sqrt{\frac{36}{49}}}=\frac{1}{\sqrt{{\left(\frac{6}{7}\right)}^2}}=\frac{1}{\frac{6}{7}}=\frac{7}{6};$

c) ${100}^{\mathrm{1,5}}={100}^{\frac{3}{2}}=\sqrt{{\left({10}^2\right)}^3}=\sqrt{{\left({10}^3\right)}^2}={10}^3=1000$.

Thực hành 4 trang 10 Toán 11 Tập 2: Viết các biểu thức sau dưới dạng lũy thừa với số mũ hữu tỉ:

a) $\sqrt{2^3}$;

b) $\sqrt[5]{\frac{1}{27}}$;

c) ${\left(\sqrt[5]{a}\right)}^4\left(a>0\right)$.

Lời giải:

a) $\sqrt{2^3}=2^{\frac{3}{2}};$

b) $\sqrt[5]{\frac{1}{27}}=\sqrt[5]{{\left(\frac{1}{3}\right)}^3}={\left(\frac{1}{3}\right)}^{\frac{3}{5}};$

c) Với a > 0, ta có ${\left(\sqrt[5]{a}\right)}^4=\sqrt[5]{a^4}=a^{\frac{4}{5}}.$

4. Lũy thừa với số mũ thực

Hoạt động khám phá 4 trang 10 Toán 11 Tập 2: Ta biết rằng, $\sqrt{2}$ là một số vô tỷ có thể biểu diễn dưới dạng số thập phân vô hạn không tuần hoàn: $\sqrt{2}=\mathrm{1,41}4213562\dots$.

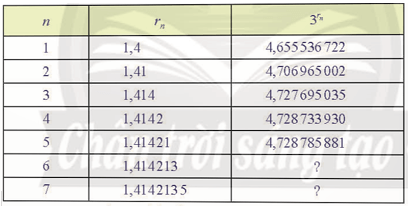
Cũng có thể coi $\sqrt{2}$ là giới hạn của dãy số hữu tỉ $\left(r_n\right)$:

$\mathrm{1,4};\mathrm{1,41};\mathrm{1,414};\mathrm{1,4142};\dots .$

Từ đây, ta lập dãy số các lũy thừa $\left(3^{r_n}\right)$.

a) Bảng dưới cho biết những số hạng đầu tiên của dãy số $\left(3^{r_n}\right)$(làm tròn đến chữ số thập phân thứ chín). Sử dụng máy tính cầm tay, hãy tính số hạng thứ 6 và thứ 7 của dãy số này.

b) Nêu nhận xét về dãy số $\left(3^{r_n}\right)$.

Lời giải:

a) Sử dụng máy tính cầm tay, ta có:

r⁶ = 3^{1,414 213} = 4,788 014 66; r⁷ = 3^{1,414 213 4} = 4,728 803 544.

b)Ta thấy khi n → +∞ thì $3^{r_n}\to 3^{\sqrt{2}}.$

Thực hành 5 trang 11 Toán 11 Tập 2: Sử dụng máy tính cầm tay, tính các lũy thừa sau đây (làm tròn đến chữ số thập phân thứ sáu):

a) ${\mathrm{1,2}}^{\mathrm{1,5}}$; b) ${10}^{\sqrt{3}}$; c) ${\left(\mathrm{0,5}\right)}^{-\frac{2}{3}}$.

Lời giải:

Sử dụng máy tính cầm tay, tính các lũy thừa sau đây (làm tròn đến chữ số thập phân thứ sáu), ta được:

a) ${\mathrm{1,2}}^{\mathrm{1,5}}\approx \mathrm{1,314534}$;

b) ${10}^{\sqrt{3}}\approx \mathrm{53,957374}$;

c) ${\left(\mathrm{0,5}\right)}^{-\frac{2}{3}}\approx \mathrm{1,587401}$.

5. Tính chất của phép tính lũy thừa

Hoạt động khám phá 5 trang 11 Toán 11 Tập 2: a) Sử dụng máy tính cầm tay, hoàn thành bảng sau vào vở (làm tròn kết quả đến chữ so thập phân thứ năm)

b) Từ kết quả ở câu a, có dự đoán gì về tính chất của phép tính lũy thừa với số mũ thực?

Phép tính lũy thừa với số mũ thực có tính chất tương tự như lũy thừa với số mũ tự nhiên.

Lời giải:

a) $a^{\alpha }.a^{\beta }=3^{\sqrt{2}}.3^{\sqrt{3}}\approx \mathrm{31,70659}$;

$a^{\alpha }:a^{\beta }=3^{\sqrt{2}}:3^{\sqrt{3}}\approx \mathrm{0,70527}$;

${a^{\alpha }}^{+\beta }={3^{\sqrt{2}+}}^{\sqrt{3}}\approx \mathrm{31,70659}$;

${a^{\alpha }}^{-\beta }={3^{\sqrt{2}-}}^{\sqrt{3}}\approx \mathrm{0,70527}$.

b) Ta thấy: $a^{\alpha }.a^{\beta }={a^{\alpha }}^{+\beta };a^{\alpha }:a^{\beta }={a^{\alpha }}^{-\beta }.$

Ta dự đoán tính chất của phép tính lũy thừa với số mũ thực có tính chất tương tự với phép tính lũy thừa với số mũ tự nhiên.

Thực hành 6 trang 12 Toán 11 Tập 2: Viết các biểu thức sau dưới dạng một lũy thừa (a > 0).

a) $a^{\frac{3}{5}}.a^{\frac{1}{2}}:a^{-\frac{2}{5}}$;

b) $\sqrt{a^{\frac{1}{2}}\sqrt{a^{\frac{1}{2}}\sqrt{a}}}$.

Lời giải:

a) $a^{\frac{3}{5}}.a^{\frac{1}{2}}:a^{-\frac{2}{5}}=a^{\frac{3}{5}+\frac{1}{2}-\left(-\frac{2}{5}\right)}=a^{\frac{3}{5}+\frac{1}{2}+\frac{2}{5}}=a^{\frac{3}{2}}$;

b) $\sqrt{a^{\frac{1}{2}}\sqrt{a^{\frac{1}{2}}\sqrt{a}}}=\sqrt{a^{\frac{1}{2}}\sqrt{a^{\frac{1}{2}}.a^{\frac{1}{2}}}}=\sqrt{a^{\frac{1}{2}}\sqrt{{a^{\frac{1}{2}}}^{+\frac{1}{2}}}}$

$=\sqrt{a^{\frac{1}{2}}\sqrt{a}}=\sqrt{a^{\frac{1}{2}}.a^{\frac{1}{2}}}=\sqrt{a}$.

Thực hành 7 trang 12 Toán 11 Tập 2: Rút gọn biểu thức: ${\left(x^{\sqrt{2}}y\right)}^{\sqrt{2}}\left(9y^{-\sqrt{2}}\right)$ (với x, y > 0).

Lời giải:

Ta có ${\left(x^{\sqrt{2}}y\right)}^{\sqrt{2}}\left(9y^{-\sqrt{2}}\right)={\left(x^{\sqrt{2}}\right)}^{\sqrt{2}}{y}^{\sqrt{2}}.9y^{-\sqrt{2}}=9{x^{\sqrt{2}.}}^{\sqrt{2}}{y}^{\sqrt{2}}{y}^{-\sqrt{2}}$

$=9{x^{\sqrt{2}.}}^{\sqrt{2}}{y^{\sqrt{2}}}^{+\left(-\sqrt{2}\right)}=9x^{\sqrt{2}.\sqrt{2}}{y}^{\sqrt{2}+\left(-\sqrt{2}\right)}=9x^2{y}^0=9x^2$.

Vận dụng 2 trang 12 Toán 11 Tập 2: Tại một vùng biển, giả sử cường độ ánh sáng I thay đổi theo độ sâu theo công thức $I=I_0{.10}^{-\mathrm{0,3}d}$, trong đó d là độ sâu (tính bằng mét) so với mặt hồ, I₀ là cường độ ánh sáng tại mặt hồ.

a) Tại độ sâu 1 m, cường độ ánh sáng gấp bao nhiêu lần I₀?

b) Cường độ ánh sáng tại độ sâu 2 m gấp bao nhiêu lần so với tại độ sâu 10 m? Làm tròn kết quả đến hai chữ số thập phân.

Lời giải:

a) Với d=1ta có: I=I₀.10^−0,3.1=I₀.10^−0,3.

Vậy tại độ sâu 1 m, cường độ ánh sáng gấp 10^−0,3lần I₀.

b) Với d=2 ta có: I=I₀.10^−0,3.2=I₀.10^−0,6

Với d=10ta có: I=I₀.10^−0,3.10=I₀.10⁻³.

Cường độ ánh sáng tại độ sâu 2 m gấp cường độ ánh sáng tại độ sâu 10 m số lần là:

(I₀.10^−0,6):(I₀.10⁻³)=10^−0,6:10⁻³=10^{−0,6−(−3)}=10^2,4≈251,19(lần)

Vậy cường độ ánh sáng tại độ sâu 2 m gấp cường độ ánh sáng tại độ sâu 10 m khoảng 251,19 lần.

Bài tập

Bài 1 trang 13 Toán 11 Tập 2: Tính giá trị các biểu thức sau:

a) ${\left(\frac{3}{4}\right)}^{-2}.3^2.{12}^0$;

b) ${\left(\frac{1}{12}\right)}^{-2}\cdot {\left(\frac{2}{3}\right)}^{-2}$;

c) ${\left(2^{-2}.5^2\right)}^{-2}:\left(5.5^{-5}\right)$.

Lời giải:

a) ${\left(\frac{3}{4}\right)}^{-2}.3^2.{12}^0=\frac{1}{{\left(\frac{3}{4}\right)}^2}.3^2.1=\frac{1}{{\left(\frac{3}{4}\right)}^2}.9=\frac{16}{9}.9=16$;

b) ${\left(\frac{1}{12}\right)}^{-2}\cdot {\left(\frac{2}{3}\right)}^{-2}=\frac{1}{\frac{1}{12}}\cdot \frac{1}{{\left(\frac{2}{3}\right)}^2}=12\cdot \frac{1}{\frac{4}{9}}=12\cdot \frac{9}{4}=27$;

c) ${\left(2^{-2}.5^2\right)}^{-2}:\left(5.5^{-5}\right)={\left(\frac{5^2}{2^2}\right)}^{-2}:\left(5^{1+(-5)}\right)$

$=\frac{1}{{\left(\frac{5^2}{2^2}\right)}^2}:5^{-4}=\frac{1}{\frac{5^4}{2^4}}:\frac{1}{5^4}=\frac{2^4}{5^4}\cdot 5^4=2^4=16$.

Bài 2 trang 13 Toán 11 Tập 2: Viết các biểu thức sau dưới dạng một luỹ thừa (a>0):

a) $3.\sqrt{3}.\sqrt[4]{3}.\sqrt[8]{3}$;

b) $\sqrt{a\sqrt{a\sqrt{a}}}$;

c) $\frac{\sqrt{a}.\sqrt[3]{a}.\sqrt[4]{a}}{{\left(\sqrt[5]{a}\right)}^3.a^{\frac{2}{5}}}$.

Lời giải:

a) $3.\sqrt{3}.\sqrt[4]{3}.\sqrt[8]{3}=3.3^{\frac{1}{2}}.3^{\frac{1}{4}}.3^{\frac{1}{8}}=3^{1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}}=3^{\frac{15}{8}}$;

b) $\sqrt{a\sqrt{a\sqrt{a}}}=\sqrt{a\sqrt{a.a^{\frac{1}{2}}}}=\sqrt{a\sqrt{a^{1+\frac{1}{2}}}}=\sqrt{a\sqrt{a^{\frac{3}{2}}}}$

$=\sqrt{a.a^{\frac{3}{4}}}=\sqrt{a^{1+\frac{3}{4}}}=\sqrt{a^{\frac{7}{4}}}=a^{\frac{7}{8}}$;

Bài 3 trang 13 Toán 11 Tập 2: Rút gọn các biểu thức sau $\left(a>\mathrm{0,}b>0\right)$:

a) $a^{\frac{1}{3}}{a}^{\frac{1}{2}}{a}^{\frac{7}{6}}$;

b) $a^{\frac{2}{3}}{a}^{\frac{1}{4}}:a^{\frac{1}{6}}$;

c) $\left(\frac{3}{2}{a}^{-\frac{3}{2}}{b}^{-\frac{1}{2}}\right)\left(-\frac{1}{3}{a}^{\frac{1}{2}}{b}^{\frac{3}{2}}\right)$.

Lời giải:

c) $\left(\frac{3}{2}{a}^{-\frac{3}{2}}{b}^{-\frac{1}{2}}\right)\left(-\frac{1}{3}{a}^{\frac{1}{2}}{b}^{\frac{3}{2}}\right)=\frac{3}{2}\cdot \left(-\frac{1}{3}\right).a^{-\frac{3}{2}+\frac{1}{2}}.b^{-\frac{1}{2}+\frac{3}{2}}$

$=-\frac{1}{2}.a^{-1}.b=-\frac{b}{2a}$.

Bài 4 trang 13 Toán 11 Tập 2: Với một chỉ vàng, giả sử người thợ lành nghề có thể dát mỏng thành lá vàng rộng 1 m² và dày khoảng ${\mathrm{1,94.10}}^{-7}m$. Đồng xu 5000 đồng dày ${\mathrm{2,2.10}}^{-3}m$. Cần chồng bao nhiêu lá vàng như trên để có độ dày bằng đồng xu loại 5000 đồng? Làm tròn kết quả đến chữ số hàng trăm.

Lời giải:

Để có độ dày bằng đồng xu loại 5000 đồng ta cần chồng bao nhiêu lá vàng như trên là:

(2,2.10⁻³):(1,94.10⁻⁷)≈11300(lá vàng)

Vậy để có độ dày bằng đồng xu loại 5000 đồng ta cần chồng khoảng 11300lá vàng như trên.

Bài 5 trang 13 Toán 11 Tập 2: Tại một xí nghiệp, công thức $P\left(t\right)=500.{\left(\frac{1}{2}\right)}^{\frac{t}{3}}$ được dùng để tính giá trị còn lại (tính theo triệu đồng) của một chiếc máy sau thời gian (tính theo năm) kể từ khi đưa vào sử dụng.

a) Tính giá trị còn lại của máy sau 2 năm; sau 2 năm 3 tháng.

b) Sau 1 năm đưa vào sử dụng, giá trị còn lại của máy bằng bao nhiêu phần trăm so với ban đầu?

Lời giải:

a) Với t = 2, ta có $P\left(2\right)=500.{\left(\frac{1}{2}\right)}^{\frac{2}{3}}\approx \mathrm{314,98}$ (triệu đồng)

Ta có 2 năm 3 tháng = 2,25 năm.

Với t = 2,25 ta có $P\left(\mathrm{2,25}\right)=500.{\left(\frac{1}{2}\right)}^{\frac{\mathrm{2,25}}{2}}\approx \mathrm{297,3}$ (triệu đồng)

Vậy giá trị còn lại sau 2 năm là 314,98 triệu đồng; giá trị còn lại sau 2 năm 3 tháng là 297,3 triệu đồng.

b) Với t = 1, ta có $P\left(1\right)=500.{\left(\frac{1}{2}\right)}^{\frac{1}{3}}\approx \mathrm{396,85}$ (triệu đồng)

Sau 1 năm đưa vào sử dụng, giá trị còn lại của máy bằng:

396,85 : 500.100 = 79,37% so với ban đầu.

Vậy sau 1 năm đưa vào sử dụng, giá trị còn lại của máy bằng 79,37% so với ban đầu.

Bài 6 trang 13 Toán 11 Tập 2: Biết rằng ${10}^{\alpha }=2;{10}^{\beta }=5$. Tính ${10}^{\alpha +\beta };{10}^{\alpha -\beta };{10}^{2\alpha };{10}^{-2\alpha };{1000}^{\beta };{\mathrm{0,01}}^{2\alpha }.$

Lời giải:

• ${10}^{\alpha +\beta }={10}^{\alpha }.{10}^{\beta }=2.5=10.$

• ${10}^{\alpha -\beta }=\frac{{10}^{\alpha }}{{10}^{\beta }}=\frac{2}{5}.$

• ${10}^{2\alpha }={\left({10}^{\alpha }\right)}^2=2^2=4.$

• ${10}^{-2\alpha }=\frac{1}{{10}^{2\alpha }}=\frac{1}{4}$

• ${1000}^{\beta }={\left({10}^3\right)}^{\beta }={\left({10}^{\beta }\right)}^3=5^3=125.$

• ${\mathrm{0,01}}^{2\alpha }={\left(\frac{1}{100}\right)}^{2\alpha }=\frac{1}{{100}^{2\alpha }}=\frac{1}{{\left({10}^2\right)}^{2\alpha }}$

$=\frac{1}{{10}^{4\alpha }}=\frac{1}{{\left({10}^{\alpha }\right)}^4}=\frac{1}{2^4}=\frac{1}{16}$.

Bài 7 trang 13 Toán 11 Tập 2: Biết rằng $4^{\alpha }=\frac{1}{5}$. Tính giá trị các biểu thức sau:

a) ${16}^{\alpha }+{16}^{-\alpha }$;

b) ${\left(2^{\alpha }+2^{-\alpha }\right)}^2$.

Lời giải:

a) ${16}^{\alpha }+{16}^{-\alpha }={16}^{\alpha }+\frac{1}{{16}^{\alpha }}={\left(4^2\right)}^{\alpha }+\frac{1}{{\left(4^2\right)}^{\alpha }}$

$={\left(4^{\alpha }\right)}^2+\frac{1}{{\left(4^{\alpha }\right)}^2}={\left(\frac{1}{5}\right)}^2+\frac{1}{{\left(\frac{1}{5}\right)}^2}=\frac{626}{25}$;

b) ${\left(2^{\alpha }+2^{-\alpha }\right)}^2={\left(2^{\alpha }\right)}^2+2.2^{\alpha }.2^{-\alpha }+{\left(2^{-\alpha }\right)}^2$

$=2^{2\alpha }+2+2^{-2\alpha }={\left(2^2\right)}^{\alpha }+2+{\left(2^2\right)}^{-\alpha }$

$=4^{\alpha }+2+4^{-\alpha }=4^{\alpha }+2+\frac{1}{4^{\alpha }}$$=\frac{1}{5}+2+\frac{1}{\frac{1}{5}}=\frac{36}{5}$.

Xem thêm các bài giải SGK Toán 11 Chân trời sáng tạo hay, chi tiết khác: