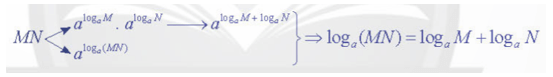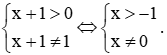Giải SGK Toán 11 (Chân trời sáng tạo) Bài 2: Phép tính lôgarit

Giải Toán 11 Bài 2: Phép tính lôgarit

Hoạt động khởi động trang 14 Toán 11 Tập 2: Thang Richter được sử dụng để đo độ lớn các trận động đất. Nếu máy đo địa chấn ghi được biên độ lớn nhất của một trận động đất là $A={10}^M\mu m$ $\left(1\mu m={10}^{-6}m\right)$thì trận động đất đó có độ lớn bằng M độ Richter. Người ta chia các trận động đất thành các mức độ như sau:

(Theo Britannica)

Đo độ lớn của động đất theo thang Richter có ý nghĩa như thế nào?

Lời giải:

Độ lớn M phải thỏa mãn hệ thức 10^M = 65 000.

1. Khái niệm lôgarit

Hoạt động khám phá 1 trang 14 Toán 11 Tập 2: Độ lớn M (theo độ Richter) của một trận động đất được xác định như Hoạt động khởi động.

a) Tìm độ lớn theo thang Richter của các trận động đất có biên độ lớn nhất lần lượt là ${10}^{\mathrm{3,5}}\mu m;100000\mu m;100{.10}^{\mathrm{4,3}}\mu m$.

b) Một trận động dất có biên độ lớn nhất A = 65 000μm thì độ lớn M của nó phải thoả mãn hệ thức nào?

Lời giải:

a) Với A = 10^3,5 μm thì M = 3,5.

Với A = 100 000μm = 10⁵ μm thì M = 5.

Với A = 100.10^4,3μm = 10².10^4,3 μm = 10^6,3 μm thì M = 6,3.

a) Với A = 65 000μm, ta có: 10^M = 65 000.

Thực hành 1 trang 15 Toán 11 Tập 2: Tính:

a) ${\log }_3\sqrt[3]{3}$;

b) ${\log }_{\frac{1}{2}}8$;

c) ${\left(\frac{1}{25}\right)}^{{\log }_{5}4}$.

Lời giải:

a) ${\log }_3\sqrt[3]{3}={\log }_3{3}^{\frac{1}{3}}=\frac{1}{3}$;

b) ${\log }_{\frac{1}{2}}8={\log }_{\frac{1}{2}}{2}^3={\log }_{\frac{1}{2}}{\left(\frac{1}{2}\right)}^{-3}=-3$;

c) ${\left(\frac{1}{25}\right)}^{{\log }_{5}4}={\left(5^{-2}\right)}^{{\log }_{5}4}={\left(5^{{\log }_{5}4}\right)}^{-2}=4^{-2}=\frac{1}{16}$.

2. Tính lôgarit bằng máy tính cầm tay

Thực hành 2 trang 16 Toán 11 Tập 2: Sử dụng máy tính cầm tay, tính giá trị các biểu thức sau (làm tròn kết quả đến chữ số thập phân thứ sáu):

a) ${\log }_5\mathrm{0,5}$;

b) $\log 25$;

c) $\ln \frac{3}{2}$.

Lời giải:

Sử dụng máy tính cầm tay, tính giá trị các biểu thức sau (làm tròn kết quả đến chữ số thập phân thứ sáu):

a) ${\log }_5\mathrm{0,5}\approx -\mathrm{0,430577}$;

b) $\log 25\approx \mathrm{1,397940}$;

c) $\ln \frac{3}{2}\approx \mathrm{0,405465}$.

3. Tính chất của phép tính lôgarit

Hoạt động khám phá 2 trang 16 Toán 11 Tập 2: Cho các số thực dương a, M, N với a ≠ 1>. Bạn Quân đã vẽ sơ đồ và tìm ra công thức biến đổi biểu thức ${\log }_a\left(MN\right)$ như sau:

a) Giải thích cách làm của bạn Quân.

b) Vẽ sơ đồ tương tự để tìm công thức biến đổi cho ${\log }_a\frac{M}{N}$ và ${\log }_a{M}^{\alpha }\left(\alpha \in ℝ\right)$ .

Lời giải:

a) Bạn Quân viết tích MN theo hai cách:

$MN=a^{{\log }_a\left(MN\right)}$ và $MN=a^{{\log }_{a}M+{\log }_{a}N}$.

Suy ra $MN=a^{{\log }_{a}M+{\log }_{a}N}=a^{{\log }_a\left(MN\right)}$.

Từ đó, nhận được ${\log }_a\left(MN\right)={\log }_{a}M+{\log }_{a}N$.

b) Tương tự $\frac{M}{N}=a^{{\log }_a\frac{M}{N}}$ và $\frac{M}{N}=\frac{a^{{\log }_{a}M}}{a^{{\log }_{a}N}}=a^{{\log }_{a}M-{\log }_{a}N}$.

Suy ra $a^{{\log }_a\frac{M}{N}}=a^{{\log }_{a}M-{\log }_{a}N}$.

Từ đó, nhận được ${\log }_a\frac{M}{N}={\log }_{a}M-{\log }_{a}N$.

Tiếp tục, có $M^{\alpha }=a^{\log {}_a{M}^{\alpha }}$ và $M^{\alpha }={\left(a^{\log {}_{a}M}\right)}^{\alpha }=a^{\alpha \log {}_{a}M}$.

Suy ra $a^{\log {}_a{M}^{\alpha }}=a^{\alpha \log {}_{a}M}$.

Từ đó, nhận được ${\log }_a{M}^{\alpha }=\alpha {\log }_{a}M$.

Thực hành 3 trang 17 Toán 11 Tập 2: Tính:

a) ${\log }_{5}4+{\log }_5\frac{1}{4}$;

b) ${\log }_{2}28-{\log }_{2}7$ ;

c) $\log \sqrt{1000}$.

Lời giải:

a) ${\log }_{5}4+{\log }_5\frac{1}{4}={\log }_5\left(4.\frac{1}{4}\right)={\log }_{5}1=0$;

b) ${\log }_{2}28-{\log }_{2}7={\log }_2\frac{28}{7}={\log }_{2}4$

$={\log }_2{2}^2=2{\log }_{2}2=2$;

c) $\log \sqrt{1000}=\log \sqrt{{10}^3}=\log {10}^{\frac{3}{2}}=\frac{3}{2}\log 10=\frac{3}{2}.$

Vận dụng trang 17 Toán 11 Tập 2: Độ lớn M của một trận động đất theo thang Richter được tính theo công thức $M=\log \frac{A}{A_0},$ trong đó A là biên độ lớn nhất ghi được bởi máy đo địa chấn, A₀ là biên độ chuẩn được sử dụng để hiệu chỉnh độ lệch gây ra bởi khoảng cách của máy đo địa chấn so với tâm chấn (ở Hoạt động khởi động và Hoạt động 1, A₀ = 1μm).

a) Tính độ lớn của trận động đất có biên độ A bằng

i) 10^5,1 A₀; ii) 65 000A₀.

b) Một trận động đất tại địa điểm N có biên độ lớn nhất gấp ba lần biên độ lớn nhất của trận động đất tại địa điểm P. So sánh độ lớn của hai trận động đất.

Lời giải:

a) i) $M=\log \frac{{10}^{\mathrm{5,1}}{A}_0}{A_0}=\log {10}^{\mathrm{5,1}}=\mathrm{5,1}$ (độ Richter);

ii) $M=\log \frac{65000A_0}{A_0}=\log 65000\approx \mathrm{4,8}$ (độ Richter).

b) Gọi M_N, M_P lần lượt là độ lớn theo thang Richter; A_N và A_P lần lượt là độ lớn nhất của trận động đất tại N và P.

Ta có

$$\begin{gathered} M_N=\log \left(\frac{A_N}{A_0}\right)+\log \left(\frac{3A_P}{A_0}\right)=\log 3+\log \frac{A_P}{A_0} \\ =\log 3+M_P\approx \mathrm{0,5}+M_P \end{gathered}$$

Vậy so với trận động đất tại P, trận động đất tại N có độ lớn hơn 0,5 độ Richter.

4. Công thức đổi cơ số

Hoạt động khám phá 3 trang 18 Toán 11 Tập 2: Khi chưa có máy tính, người ta thường tính các logarit dựa trên bảng giá trị logarit thập phân đã được xây dựng sẵn. Chẳng hạn, để tính x = log₂15, người ta viết 2^x = 15, rồi lấy logarit thập phân hai vế, nhận được $x\log 2=\log 15$ hay $x=\frac{\log 15}{\log 2}$.

Sử dụng cách làm này, tính ${\log }_{a}N$ theo $\log a$ và $\log N$ với a, N > 0, a ≠ 1.

Lời giải:

Đặt $x=lo{g}_{a}N\iff a^x=N\iff log{a}^x=logN$

$\iff xloga=logN\iff x=\frac{logN}{loga}$.

Vậy $log{}_{a}N=\frac{logN}{loga}$.

Thực hành 4 trang 18 Toán 11 Tập 2: Tính giá trị các biểu thức sau:

a) ${\log }_{\frac{1}{4}}8$;

b) ${\log }_{4}5.{\log }_{5}6.{\log }_{6}8$.

Lời giải:

a) ${\log }_{\frac{1}{4}}8=\frac{{\log }_{2}8}{{\log }_2\frac{1}{4}}=\frac{{\log }_2{2}^3}{{\log }_2{2}^{-2}}=\frac{3{\log }_{2}2}{-2{\log }_{2}2}=\frac{3}{-2}$;

b) ${\log }_{4}5.{\log }_{5}6.{\log }_{6}8={\log }_{4}5.\frac{{\log }_{4}6}{{\log }_{4}5}.{\log }_{6}8$

$={\log }_{4}6.{\log }_{6}8={\log }_{4}6.\frac{{\log }_{4}8}{{\log }_{4}6}={\log }_{4}8={\log }_{2^2}{2}^3$

$=\frac{3}{2}{\log }_{2}2=\frac{3}{2}$.

Thực hành 5 trang 18 Toán 11 Tập 2: Đặt ${\log }_{3}2=a,{\log }_{3}7=b$. Biểu thị ${\log }_{12}21$ theo a và b.

Lời giải:

${\log }_{12}21=\frac{{\log }_{3}21}{{\log }_{3}12}=\frac{{\log }_3\left(3.7\right)}{{\log }_3\left(3.2^2\right)}$

$=\frac{{\log }_{3}3+{\log }_{3}7}{{\log }_{3}3+2{\log }_{3}2}=\frac{1+b}{1+2a}$.

Bài tập

Bài 1 trang 19 Toán 11 Tập 2: Tính giá trị các biểu thức sau:

a) $lo{g}_{2}16$;

b) ${\log }_3\frac{1}{27}$;

c) $\log 1000$;

d) $9^{{\log }_{3}12}$.

Lời giải:

a) $lo{g}_{2}16=lo{g}_2{2}^4=4$;

b) ${\log }_3\frac{1}{27}={\log }_3{3}^{-3}=-3$;

c) $\log 1000=\log {10}^3=3$;

d) $9^{{\log }_{3}12}=3^{2{\log }_{3}12}={\left(3^{{\log }_{3}12}\right)}^2={12}^2=144$.

Bài 2 trang 19 Toán 11 Tập 2: Tìm các giá trị của x đề biểu thức sau có nghĩa:

a) ${\log }_3(1-2x)$;

b) ${\log }_{x+1}5$.

Lời giải:

a) ${\log }_3(1-2x)$ có nghĩa khi $1-2x>0\iff 2x<1\iff x<\frac{1}{2}$.

b) ${\log }_{x+1}5$ có nghĩa khi 

Bài 3 trang 19 Toán 11 Tập 2: Sử dụng máy tính cầm tay, tính giá trị các biểu thức sau (làm tròn kết quả đến chữ số thập phân thứ tư):

a) ${\log }_{3}15$;

b) $\log 8-\log 3$;

c) $3\ln 2$.

Lời giải:

Sử dụng máy tính cầm tay, ta tính được giá trị các biểu thức (làm tròn kết quả đến chữ số thập phân thứ tư) như sau:

a) ${\log }_{3}15\approx \mathrm{2,4650}$;

b) $\log 8-\log 3=\log \frac{8}{3}\approx \mathrm{0,4260}$;

c) $3\ln 2\approx \mathrm{2,0794}$.

Bài 4 trang 19 Toán 11 Tập 2: Tính giá trị các biểu thức sau:

a) ${\log }_{6}9+{\log }_{6}4$;

b) ${\log }_{5}2-{\log }_{5}50$;

c) ${\log }_3\sqrt{5}-\frac{1}{2}{\log }_{3}15$.

Lời giải:

a) ${\log }_{6}9+{\log }_{6}4={\log }_6\left(9.4\right)={\log }_{6}36$

$={\log }_6{6}^2=2{\log }_{6}6=2$;

b) ${\log }_{5}2-{\log }_{5}50={\log }_5\frac{2}{50}={\log }_5\frac{1}{25}$

$={\log }_5{5}^{-2}=-2{\log }_{5}5=-2$;

c) ${\log }_3\sqrt{5}-\frac{1}{2}{\log }_{3}15={\log }_3{5}^{\frac{1}{2}}-\frac{1}{2}{\log }_{3}15$

$=\frac{1}{2}{\log }_{3}5-\frac{1}{2}{\log }_{3}15=\frac{1}{2}{\log }_3\frac{5}{15}=\frac{1}{2}{\log }_3\frac{1}{3}$

$=\frac{1}{2}{\log }_3{3}^{-1}=-\frac{1}{2}{\log }_{3}3=-\frac{1}{2}$.

Bài 5 trang 19 Toán 11 Tập 2: Tính giá trị các biểu thức sau:

a) ${\log }_{2}9.{\log }_{3}4$;

b) ${\log }_{25}\frac{1}{\sqrt{5}}$;

c) ${\log }_{2}3.{\log }_9\sqrt{5}.{\log }_{5}4$.

Lời giải:

a) ${\log }_{2}9.{\log }_{3}4={\log }_2{3}^2.{\log }_3{2}^2=2.2.{\log }_{2}3.{\log }_{3}2$

$=4.\frac{1}{{\log }_{3}2}.{\log }_{3}2=4$;

b) ${\log }_{25}\frac{1}{\sqrt{5}}={\log }_{5^2}{5}^{\frac{1}{2}}=-\frac{1}{2}\cdot \frac{1}{2}{\log }_{5}5=-\frac{1}{4}$;

c) ${\log }_{2}3.{\log }_9\sqrt{5}.{\log }_{5}4={\log }_{2}3.{\log }_{3^2}{5}^{\frac{1}{2}}.{\log }_5{2}^2$

$={\log }_{2}3.\frac{1}{2}\cdot \frac{1}{2}.{\log }_{3}5.2{\log }_{5}2=\frac{1}{2}{\log }_{2}3.{\log }_{3}5.{\log }_{5}2$

$=\frac{1}{2}{\log }_{2}3.\frac{{\log }_{2}5}{{\log }_{2}3}.{\log }_{5}2=\frac{1}{2}{\log }_{2}5.{\log }_{5}2$

$=\frac{1}{2}{\log }_{2}5.\frac{1}{{\log }_{2}5}=\frac{1}{2}$.

Bài 6 trang 19 Toán 11 Tập 2: Đặt $\log 2=a,\log 3=b$. Biểu thị các biểu thức sau theo a và b.

a) ${\log }_{4}9$;

b) ${\log }_{6}12$;

c) ${\log }_{5}6$.

Lời giải:

a) ${\log }_{4}9=\frac{\log 9}{\log 4}=\frac{\log 3^2}{\log 2^2}=\frac{2\log 3}{2\log 2}=\frac{b}{a}$;

b) ${\log }_{6}12=\frac{\log 12}{\log 6}=\frac{\log \left(2^2.3\right)}{\log \left(2.3\right)}=\frac{2\log 2+\log 3}{\log 2+\log 3}=\frac{2a+b}{a+b}$;

c) ${\log }_{5}6=\frac{\log 6}{\log 5}=\frac{\log \left(2.3\right)}{\log \frac{10}{2}}=\frac{\log 2+\log 3}{1-\log 2}=\frac{a+b}{1-a}$.

Bài 7 trang 19 Toán 11 Tập 2: a) Nước cất có nồng độ H⁺ là ${10}^{-7}\text{mol}/\text{L}$. Tính độ pH của nước cất.

b) Một dung dịch có nồng độ H⁺ gấp 20 lần nồng độ H⁺ của nước cất. Tính độ pH của dung dịch đó.

Lời giải:

a) Độ pH của nước cất là $-\log \left({10}^{-7}\right)=7$.

b) Dung dịch có nồng độ H⁺ gấp 20 lần nồng độ H⁺ của nước cất thì cópHlà:

$-\log \left(20.{10}^{-7}\right)=-\log \left(2.{10}^{-6}\right)=-\log 2+6\approx \mathrm{5,7.}$

Xem thêm các bài giải SGK Toán 11 Chân trời sáng tạo hay, chi tiết khác: