Vẽ đồ thị các hàm số sau: a) y = x^2 – 4x + 3; b) y = - x^2 – 4x + 5

Bài 3 trang 59 Toán lớp 10 Tập 1: Vẽ đồ thị các hàm số sau:

a) y = x² – 4x + 3;

b) y = - x² – 4x + 5;

c) y = x² – 4x + 5;

d) y = -x² – 2x – 1.

Trả lời

a) Xét hàm số y = x² – 4x + 3, ta có:

Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = f(x) = x² – 4x + 3 là một parabol (P):

– Có đỉnh S với hoành độ x_S = 2, tung độ y_S­ = –1;

– Có trục đối xứng là đường thẳng x = 2 (đường thẳng này đi qua đỉnh S và song song với trục Oy);

– Bề lõm quay lên trên vì a > 0;

– Cắt trục tung tại điểm có tung độ bằng 3, tức là đồ thị đi qua điểm có tọa độ (0; 3);

– Ngoài ra, phương trình x² – 4x + 3 = 0 có hai nghiệm phân biệt là x₁ = 1, x₂ = 3. Do đó, đồ thị còn đi qua hai điểm (1; 0), (3; 0).

Ta vẽ được đồ thị như hình dưới:

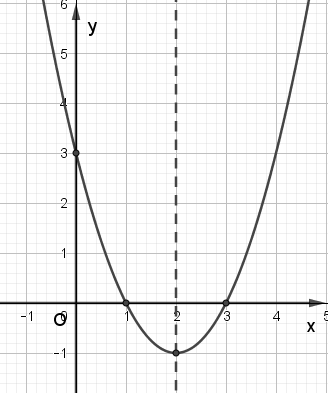
b) Xét hàm số y = –x² – 4x + 5, ta có:

Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = f(x) = –x² – 4x + 5 là một parabol (P):

– Có đỉnh S với hoành độ x_S = –2, tung độ y_S­ = 9;

– Có trục đối xứng là đường thẳng x = –2 (đường thẳng này đi qua đỉnh S và song song với trục Oy);

– Bề lõm quay xuống dưới vì a < 0;

– Cắt trục tung tại điểm có tung độ bằng 5, tức là đồ thị đi qua điểm có tọa độ (0; 5);

– Ngoài ra, phương trình –x² – 4x + 5 = 0 có hai nghiệm phân biệt là x₁ = –5, x₂ = 1. Do đó, đồ thị còn đi qua hai điểm (–5; 0), (1; 0).

Ta vẽ được đồ thị như hình dưới:

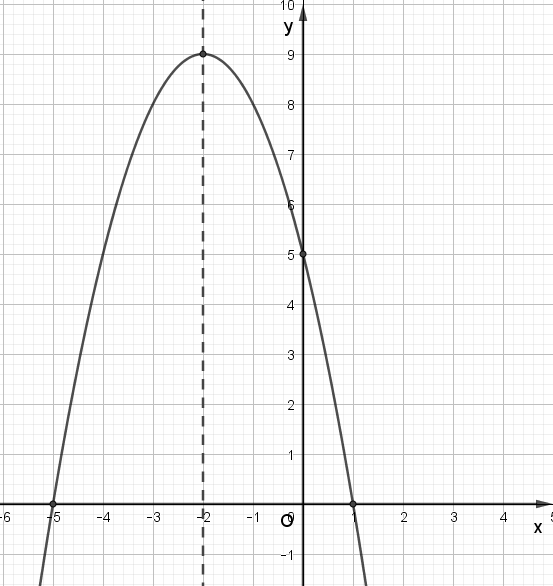
c) Xét hàm số y = x² – 4x + 5, ta có:

Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = f(x) = x² – 4x + 5 là một parabol (P):

– Có đỉnh S với hoành độ x_S = 2, tung độ y_S­ = 1;

– Có trục đối xứng là đường thẳng x = 1 (đường thẳng này đi qua đỉnh S và song song với trục Oy);

– Bề lõm quay lên trên vì a > 0;

– Cắt trục tung tại điểm có tung độ bằng 5, tức là đồ thị đi qua điểm có tọa độ (0; 5);

– Ngoài ra, đồ thị hàm số y = x² – 4x + 5 còn đi qua điểm (4; 5).

Ta vẽ được đồ thị như hình dưới:

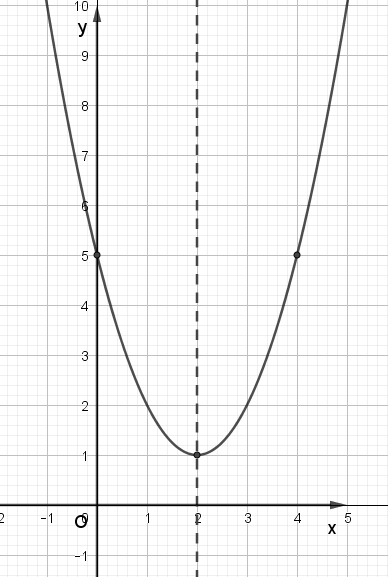
d) Xét hàm số y = –x² – 2x – 1, ta có:

Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = f(x) = –x² – 2x – 1 là một parabol (P):

– Có đỉnh S với hoành độ x_S = –1, tung độ y_S­ = 0;

– Có trục đối xứng là đường thẳng x = –1 (đường thẳng này đi qua đỉnh S và song song với trục Oy);

– Bề lõm quay xuống dưới vì a < 0;

– Cắt trục tung tại điểm có tung độ bằng –1, tức là đồ thị đi qua điểm có tọa độ (0; –1);

– Ngoài ra, đồ thị hàm số y = –x² – 2x – 1 còn đi qua hai điểm (–3; –4) và (1; –4).

Ta vẽ được đồ thị như hình dưới:

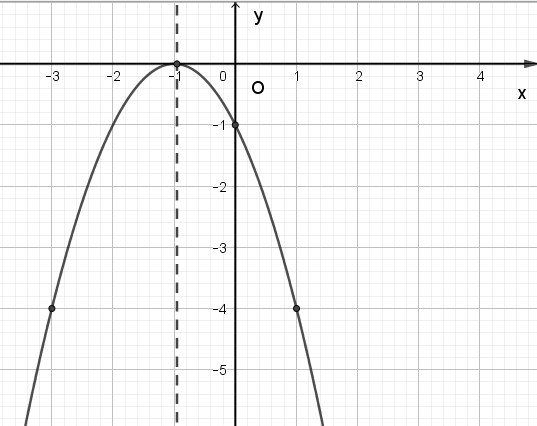
Xem thêm lời giải bài tập SGK Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Bài 1: Hàm số và đồ thị

Bài 2: Hàm số bậc hai

Bài tập cuối chương 3

Bài 1: Giá trị lượng giác của một góc từ 0 độ đến 180 độ

Bài 2: Định lí côsin và định lí sin

Bài 3: Giải tam giác và ứng dụng thực tế