Giải SGK Toán 10 (Kết nối tri thức) Bài 18: Phương trình quy về phương trình bậc hai

Giải Toán 10 Bài 18: Phương trình quy về phương trình bậc hai

1. Phương trình dạng $\sqrt{a{x}^2+bx+c}=\sqrt{d{x}^2+ex+f}$

HĐ1 trang 25 Toán 10 Tập 2: Cho phương trình $\sqrt{x^2-3x+2}=\sqrt{-x^2-2x+2}$. 

a) Bình phương hai vế phương trình để khử căn và giải phương trình nhận được. 

b) Thử lai các giá trị x tìm được ở câu a có thỏa mãn phương trình đã cho hay không?

Lời giải:

a) Bình phương hai vế của phương trình $\sqrt{x^2-3x+2}=\sqrt{-x^2-2x+2}$ ta được: 

x² – 3x + 2 = – x² – 2x + 2 (1)

Giải phương trình trên ta có: 

(1) ⇔ 2x² – x = 0 

⇔ x(2x – 1) = 0 

⇔ x = 0 hoặc 2x – 1 = 0 

⇔ x = 0 hoặc x = $\frac{1}{2}$

b) Thử lại ta có: 

+ Với x = 0, thay vào phương trình đã cho ta được: 

 $\sqrt{0^2-3.0+2}=\sqrt{-0^2-2.0+2}\iff \sqrt{2}=\sqrt{2}$(luôn đúng). 

+ Với x = $\frac{1}{2}$, thay vào phương trình đã cho ta được: 

$\sqrt{{\left(\frac{1}{2}\right)}^2-3.\frac{1}{2}+2}=\sqrt{-{\left(\frac{1}{2}\right)}^2-2.\frac{1}{2}+2}\iff \sqrt{\frac{3}{4}}=\sqrt{\frac{3}{4}}$(luôn đúng)

Vậy các giá trị x tìm được ở câu a thỏa mãn phương trình đã cho. 

Luyện tập 1 trang 25 Toán 10 Tập 2: Giải các phương trình sau: 

a) $\sqrt{3x^2-6x+1}=\sqrt{-2x^2-9x+1}$;

b) $\sqrt{2x^2-3x-5}=\sqrt{x^2-7}$.

Lời giải:

a) $\sqrt{3x^2-6x+1}=\sqrt{-2x^2-9x+1}$

Bình phương hai vế của phương trình trên ta được, 

3x² – 6x + 1 = –2x² – 9x + 1.

Thu gọn phương trình trên ta được: 5x² + 3x = 0 ⇔ x(5x + 3) = 0 ⇔ x = 0 hoặc x = $-\frac{3}{5}$. 

Thay lần lượt hai giá trị này của x vào phương trình đã cho, ta thấy cả hai giá trị x = 0 và x = $-\frac{3}{5}$ đều thỏa mãn. 

Vậy tập nghiệm của phương trình đã cho là S = $\left\{0;-\frac{3}{5}\right\}$.

b) $\sqrt{2x^2-3x-5}=\sqrt{x^2-7}$

Bình phương hai vế của phương trình trên ta được, 

2x² – 3x – 5 = x² – 7.

Thu gọn ta được: x² – 3x + 2 = 0. 

Giải phương trình bậc hai x² – 3x + 2 = 0 tìm được x = 1 hoặc x = 2. 

Thay lần lượt giá trị của x vào phương trình đã cho, ta thấy không có giá trị nào của x thỏa mãn. 

Vậy phương trình đã cho vô nghiệm. 

2. Phương trình dạng $\sqrt{a{x}^2+bx+c}=dx + e$

HĐ2 trang 25 Toán 10 Tập 2: Cho phương trình $\sqrt{26x^2-63x+38}=5x-6$. 

a) Bình phương hai vế và giải phương trình nhận được. 

b) Thử lại các giá trị x tìm được ở câu a có thỏa mãn phương trình hay không?

Lời giải:

a) Bình phương hai vế của phương trình đã cho ta được: 

26x² – 63x + 38 = 25x² – 60x + 36      (1). 

Giải phương trình (1). 

Ta có: (1) ⇔ x² – 3x + 2 = 0 ⇔ x = 1 hoặc x = 2. 

b) Thử lại

+ Với x = 1 thay vào phương trình đã cho ta được:$\sqrt{{26.1}^2-63.1+38}=5.1-6$

$\iff \sqrt{1}=–1$(vô lí).

+ Với x = 2 thay vào phương trình đã cho ta được: $\sqrt{{26.2}^2-63.2+38}=5.2-6$

$\iff \sqrt{16}=4$⇔ 4 = 4 (luôn đúng)

Vậy giá trị x = 2 thỏa mãn phương trình đã cho. 

Luyện tập 2 trang 26 Toán 10 Tập 2: Giải các phương trình sau:

a) $\sqrt{2x^2+x+3}=1-x$;

b) $\sqrt{3x^2-13x+14}=x-3$. 

Lời giải:

a) $\sqrt{2x^2+x+3}=1-x$

Bình phương hai vế của phương trình ta được

2x² + x + 3 = 1 – 2x + x².

Thu gọn ta được: x² + 3x + 2 = 0 ⇔ x² + x + 2x + 2 = 0 ⇔ x(x + 1) + 2(x + 1) = 0 

⇔ (x + 1)(x + 2) = 0 ⇔ x = – 1 hoặc x = – 2. 

Thay lần lượt hai giá trị này của x vào phương trình đã cho, ta thấy cả hai giá trị x = – 1 và x = – 2 đều thỏa mãn.

Vậy tập nghiệm của phương trình đã cho là S = {– 1; – 2}.

b) $\sqrt{3x^2-13x+14}=x-3$

Bình phương hai vế của phương trình ta được

3x² – 13x + 14 = x² – 6x + 9.

Thu gọn ta được: 2x² – 7x + 5 = 0. 

Giải phương trình bậc hai này ta được x = 1 hoặc x = $\frac{5}{2}$. 

Thay lần lượt hai giá trị này của x vào phương trình đã cho, ta thấy cả hai giá trị đều không thỏa mãn. 

Vậy phương trình đã cho vô nghiệm. 

Vận dụng trang 26 Toán 10 Tập 2: Bác Việt sống và làm việc tại trạm hải đăng cách bờ biển 4 km. Hằng tuần bác chèo thuyền vào vị trí gần nhất trên bờ biển là bến Bính để nhận hàng hóa do cơ quan cung cấp. Tuần này, do trục trặc về vận chuyển nên toàn bộ số hàng vẫn đang nằm ở thôn Hoành, bên bờ biển cách bến Bính 9,25 km và sẽ được anh Nam vận chuyển trên con đường dọc bờ biển tới bến Bính bằng xe kéo. Bác Việt đã gọi điện thống nhất với anh Nam là họ sẽ gặp nhau ở vị trí nào đó giữa bến Bính và thôn Hoành để hai người có mặt tại đó cùng lúc, không mất thời gian chờ nhau. Giả thiết rằng đường dọc bờ biển là thẳng và bác Việt cũng di chuyển theo một đường thẳng để tới điểm hẹn. Tìm vị trí hai người hẹn gặp, biết rằng vận tốc của anh Nam là 5 km/h và của bác Việt là 4 km/h. 

Hướng dẫn 

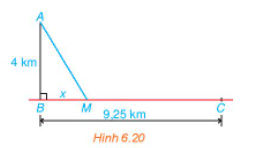
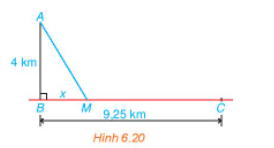
Ta mô hình hóa bài toán như trong Hình 6.20: Trạm hải đăng ở vị trí A; bến Bính ở B và thôn Hoành ở C. 

Giả sử bác Việt chèo thuyền cập bến ở vị trí M và ta đặt BM = x (km) (x > 0). Để hai người không phải chờ nhau thì thời gian chèo thuyền bằng thời gian kéo xe nên ta có phương trình: 

$\frac{\sqrt{x^2+16}}{4}=\frac{\mathrm{9,25}-x}{5}$. 

Giải phương trình này sẽ tìm được vị trí hai người dự định gặp nhau. 

Lời giải:

Ta mô hình hóa bài toán như trong Hình 6.20: Trạm hải đăng ở vị trí A; bến Bính ở B và thôn Hoành ở C. 

Giả sử bác Việt chèo thuyền cập bến ở vị trí M và ta đặt BM = x (km) (x > 0).

Ta có: BC = BM + MC ⇔ MC = BC – BM = 9,25 – x (km) hay quãng đường của anh Nam từ thôn Hoành đến điểm gặp nhau của 2 người là 9,25 – x (km). 

Vận tốc của anh Nam là 5 km/h nên thời gian di chuyển của anh Nam đến điểm hẹn gặp nhau là: $\frac{\mathrm{9,25}-x}{5}$(giờ). 

Tam giác ABC vuông tại B, theo định lí Pythagore ta có: 

AM² = AB² + BM² = 4² + x² = x² + 16 

Suy ra AM = $\sqrt{x^2+16}$(km) hay quãng đường di chuyển của bác Việt đến điểm hẹn là (km). 

Vận tốc của bác Việt là 4 km/h nên thời gian di chuyển của bác Việt tới điểm hẹn gặp nhau là: $\frac{\sqrt{x^2+16}}{4}$(giờ). 

Để hai người không phải chờ nhau thì thời gian chèo thuyền bằng thời gian kéo xe nên ta có phương trình: 

$\frac{\sqrt{x^2+16}}{4}=\frac{\mathrm{9,25}-x}{5}$(1). 

Giải phương trình trên ta có: 

(1)$\iff 5\sqrt{x^2+16}=37-4x$

Bình phương hai vế phương trình trên ta được:

25(x² + 16) = 1369 – 296x + 16x² 

⇔ 9x² + 296x – 969 = 0 

⇔ x = 3 hoặc x = $-\frac{323}{9}$

Thử lại ta thấy cả hai giá trị x = 3 và x = $-\frac{323}{9}$ đều thỏa mãn phương trình (1). 

 Mà điều kiện của x là x > 0 nên ta chọn x = 3. 

Vậy vị trí hai người hẹn gặp nhau cách bến Bính 3 km hay cách thôn Hoành 6,25 km.

Bài tập

Bài 6.20 trang 27 Toán 10 Tập 2: Giải các phương trình sau: 

a) $\sqrt{3x^2-4x-1}=\sqrt{2x^2-4x+3}$;

b) $\sqrt{x^2+2x-3}=\sqrt{-2x^2+5}$; 

c) $\sqrt{2x^2+3x-3}=\sqrt{-x^2-x+1}$;

d) $\sqrt{-x^2+5x-4}=\sqrt{-2x^2+4x+2}$. 

Lời giải:

 a)$\sqrt{3x^2-4x-1}=\sqrt{2x^2-4x+3}$

Bình phương hai vế của phương trình ta được: 

3x²– 4x – 1 = 2x² – 4x + 3 

⇔ x² – 4 = 0 

⇔ x² = 4 

⇔   x = 2 hoặc x = – 2. 

Thay lần lượt các giá trị này vào phương trình đã cho, ta thấy cả hai giá trị x = 2 và x = – 2 thỏa mãn. 

Vậy tập nghiệm của phương trình là S = {– 2; 2}.

b) $\sqrt{x^2+2x-3}=\sqrt{-2x^2+5}$

Bình phương hai vế của phương trình ta được: 

x² + 2x – 3 = – 2x² + 5 

⇔ 3x² + 2x – 8 = 0 

⇔ x = – 2 hoặc x = $\frac{4}{3}$. 

Thay lần lượt các giá trị này vào phương trình đã cho, ta thấy chỉ có giá trị x = $\frac{4}{3}$ thỏa mãn. 

Vậy nghiệm của phương trình là x = $\frac{4}{3}$. 

c) $\sqrt{2x^2+3x-3}=\sqrt{-x^2-x+1}$

Bình phương hai vế của phương trình ta được: 

2x² + 3x – 3 = – x² – x + 1 

⇔ 3x² + 4x – 4 = 0 

⇔ x = – 2 hoặc x = $\frac{2}{3}$. 

Thay lần lượt các giá trị này vào phương trình đã cho, ta thấy cả hai giá trị đều không thỏa mãn. 

Vậy phương trình vô nghiệm. 

d) $\sqrt{-x^2+5x-4}=\sqrt{-2x^2+4x+2}$

Bình phương hai vế của phương trình ta được: 

– x² + 5x – 4 = – 2x² + 4x + 2 

⇔ x² + x – 6 = 0 

⇔ x = – 3 hoặc x = 2. 

Thay lần lượt các giá trị này vào phương trình đã cho, ta thấy x = 2 thỏa mãn. 

Vậy nghiệm của phương trình là x = 2. 

Bài 6.21 trang 27 Toán 10 Tập 2: Giải các phương trình sau: 

a) $\sqrt{6x^2+13x+13}=2x+4$; 

b) $\sqrt{2x^2+5x+3}=-3-x$; 

c) $\sqrt{3x^2-17x+23}=x-3$; 

d) $\sqrt{-x^2+2x+4}=x-2$

Lời giải:

a) $\sqrt{6x^2+13x+13}=2x+4$

Bình phương hai vế của phương trình ta được

 6x²+ 13x + 13 = 4x² + 16x + 16 

⇔ 2x² – 3x – 3 = 0 

⇔ x = $\frac{3-\sqrt{33}}{4}$ hoặc x = $\frac{3+\sqrt{33}}{4}$.

Thay lần lượt các giá trị này vào phương trình đã cho, ta thấy cả hai giá trị x = $\frac{3-\sqrt{33}}{4}$ và x = $\frac{3+\sqrt{33}}{4}$ đều thỏa mãn. 

Vậy tập nghiệm của phương trình là S = $\left\{\frac{3-\sqrt{33}}{4};\frac{3+\sqrt{33}}{4}\right\}$. 

b) $\sqrt{2x^2+5x+3}=-3-x$

Bình phương hai vế của phương trình ta được

2x² + 5x + 3 = 9 + 6x + x²

⇔ x² – x – 6 = 0 

⇔ x = – 2 hoặc x = 3.

Thay lần lượt các giá trị này vào phương trình đã cho, ta thấy không có giá trị nào thỏa mãn. 

Vậy phương trình vô nghiệm. 

c) $\sqrt{3x^2-17x+23}=x-3$

Bình phương hai vế của phương trình ta được

3x² – 17x + 23 = x² – 6x + 9  

⇔ 2x² – 11x + 14 = 0 

⇔ x = 2 hoặc x = $\frac{7}{2}$. 

Thay lần lượt các giá trị này vào phương trình đã cho, ta thấy x = $\frac{7}{2}$ thỏa mãn. 

Vậy nghiệm của phương trình là x = $\frac{7}{2}$. 

d) $\sqrt{-x^2+2x+4}=x-2$

Bình phương hai vế của phương trình ta được

– x² + 2x + 4 = x² – 4x + 4 

⇔ – 2x² + 6x = 0 

⇔ – 2x(x – 3) = 0

⇔ x = 0 hoặc x = 3.

Thay lần lượt các giá trị này vào phương trình đã cho, ta thấy x = 3 thỏa mãn. 

Vậy nghiệm của phương trình là x = 3. 

Bài 6.22 trang 27 Toán 10 Tập 2: Cho tứ giác ABCD có AB ⊥ CD; AB = 2; BC = 13; CD = 8; DA = 5 (H.6.21). Gọi H là giao điểm của AB và CD và đặt x = AH. Hãy thiết lập một phương trình để tính độ dài x, từ đó tính diện tích tứ giác ABCD. 

Lời giải:

Đặt AH = x, x > 0. 

Xét tam giác AHD vuông tại H, theo định lí Pythagore ta có: 

AD² = AH² + HD² ⇔ HD² = AD² – AH² = 5² – x² = 25 – x² 

Suy ra HD = $\sqrt{25-x^2}$.

Ta có HC = HD + DC = $\sqrt{25-x^2} + 8$. 

HB = AH + AB = x + 2 

Xét tam giác HBC vuông tại H, theo định lí Pythagore ta có: 

BC² = HB² + HC² 

⇔ 13² = (x + 2)² + ${\left(\sqrt{25-x^2}+8\right)}^2$

⇔ x² + 4x + 4 + 25 – x² + 16$\sqrt{25-x^2}$+ 64 – 169 = 0

⇔ 16$\sqrt{25-x^2}$ = – 4x + 76 

⇔ 4$\sqrt{25-x^2}$ = – x + 19  

Để tính x, ta cần giải phương trình: 4$\sqrt{25-x^2}$ = – x + 19 (1). 

Bình phương hai vế của phương trình (1) ta được: 

16.(25 – x²) = x² – 38x + 361

⇔ 17x² – 38x – 39 = 0  

⇔ x = 3 hoặc x = $-\frac{13}{17}$. 

Thay lần lượt các giá trị trên vào phương trình (1), ta thấy hai giá trị x = 3 và x = $-\frac{13}{17}$  đều thỏa mãn. 

Vì điều kiện của x là x > 0 nên ta chọn x = 3. 

Do đó ta tính được AH = 3. 

Suy ra HD = $\sqrt{25-3^2}=4$.

HC = 4 + 8 = 12

HB = 3 + 2 = 5

Diện tích tam giác HAD là S₁ = $\frac{1}{2}$HA . HD = $\frac{1}{2}$. 3 . 4 = 6. 

Diện tích tam giác HBC là S₂ = $\frac{1}{2}$HB . HC = $\frac{1}{2}$. 5 . 12 = 30.

Vậy diện tích tứ giác ABCD là S = S₂ – S₁ = 30 – 6 = 24.  

Bài 6.23 trang 27 Toán 10 Tập 2: Hằng ngày bạn Hùng đều đón bạn Minh đi học tại một vị trí trên lề đường thẳng đến trường. Minh đứng tại vị trí A cách lề đường một khoảng 50 m để chờ Hùng. Khi nhìn thấy Hùng đạp xe đến địa điểm B, cách mình một đoạn 200 m thì Minh bắt đầu đi bộ ra lề đường để bắt kịp xe. Vận tốc đi bộ của Minh là 5 km/h, vận tốc xe đạp của Hùng là 15 km/h. Hãy xác định vị trí C trên lề đường (H.6.22) để hai bạn gặp nhau mà không bạn nào phải chờ người kia (làm tròn kết quả đến hàng phần mười). 

Lời giải:

Đổi: 200 m = 0,2 km, 50 m = 0,05 km.

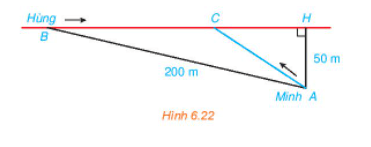
Ta mô hình hóa bài toán như trong hình vẽ sau:

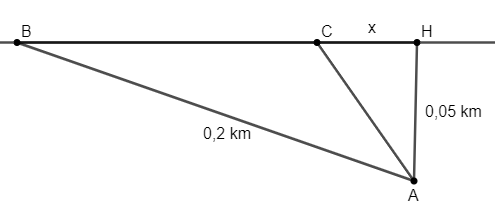
Hùng ở vị trí B, Minh ở vị trí A, H là vị trí lề đường mà Minh đi theo hướng vuông góc với BC từ vị trí A.

Giả sử C là vị trí Hùng và Minh gặp nhau. Đặt CH = x (km) (x > 0).

Áp dụng định lí Pythagore tam giác HAB vuông tại H, ta có:

AB² = HB² + HA² ⇔ HB² = AB² – HA² = (0,2)² – (0,05)² = 0,0375

Suy ra HB = $\frac{\sqrt{15}}{20}$.

Ta có: BC + CH = HB ⇔ BC = HB – CH = $\frac{\sqrt{15}}{20}-x$.

Do đó quãng đường di chuyển của Hùng từ B đến điểm gặp nhau C dài $\frac{\sqrt{15}}{20}-x$ (km).

Vận tốc đạp xe của Hùng là 15 km/h nên thời gian di chuyển của Hùng từ B đến điểm gặp nhau là: $\frac{\frac{\sqrt{15}}{20}-x}{15}=\frac{\sqrt{15}-20x}{300}$ (giờ).

Áp dụng định lí Pythagore trong tam giác CHA vuông tại H, ta có:

CA²= HA² + HC² = (0,05)² + x² = 0,0025 + x²

Suy ra CA = $\sqrt{\mathrm{0,0025}+x^2}$ hay quãng đường di chuyển của Minh từ vị trí A đến điểm gặp nhau C dài $\sqrt{\mathrm{0,0025}+x^2}$ (km).

Vận tốc đi bộ của Minh là 5 km/h nên thời gian di chuyển của Minh từ vị trí A đến điểm gặp nhau C là: $\frac{\sqrt{\mathrm{0,0025}+x^2}}{5}$ (giờ).

Để hai bạn gặp nhau mà không bạn nào phải chờ người kia thì thời gian di chuyển từ vị trí A đến C của Minh phải bằng thời gian di chuyển từ vị trí B đến C của Hùng.

Khi đó ta có phương trình: $\frac{\sqrt{\mathrm{0,0025}+x^2}}{5}=\frac{\sqrt{15}-20x}{300}$ (*).

Giải phương trình (*) ta có:

(*) $\iff 60\sqrt{\mathrm{0,0025}+x^2}=\sqrt{15}-20x$

Bình phương hai vế của phương trình trên ta được:

3600.(0,0025 + x²) = 15 – 40$\sqrt{15}$x + 400x²

⇔ 3200x² + 40$\sqrt{15}$x – 6 = 0

⇔ x = $\frac{-\sqrt{15}-3\sqrt{7}}{160}$ hoặc x = $\frac{-\sqrt{15}+3\sqrt{7}}{160}$.

Thay lần lượt các giá trị này vào phương trình (*) ta thấy cả hai giá trị đều thỏa mãn.

Lại có điều kiện của x là x > 0 nên ta chọn x = $\frac{-\sqrt{15}+3\sqrt{7}}{160}$≈ 0,0254.

Suy ra CH = x ≈ 0,0254 km = 25,4 m.

Do đó, BC = BH – CH ≈ $\frac{\sqrt{15}}{20}-\mathrm{0,0254}\approx \mathrm{0,1682}$km = 168,2 m.

Vậy vị trí C thỏa mãn yêu cầu đề bài là điểm cách H một khoảng 25,4 m hay C cách B một khoảng 168,2 m.

Xem thêm lời giải bài tập SGK Toán lớp 10 Kết nối tri thức hay, chi tiết khác:

Bài tập cuối chương 6 trang 28, 29

Bài 19: Phương trình đường thẳng

Bài 20: Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách

Bài 21: Đường tròn trong mặt phẳng tọa độ

Bài 22: Ba đường conic