Cho tam giác ABC vuông tại A có AB ngắn hơn AC là 2cm. Biểu diễn độ dài cạnh huyền BC theo AB
736
13/06/2023
Bài 3 trang 17 Toán lớp 10 Tập 2: Cho tam giác ABC vuông tại A có AB ngắn hơn AC là 2cm.
a) Biểu diễn độ dài cạnh huyền BC theo AB.
b) Biết chu vi của tam giác ABC là 24 cm. Tìm độ dài ba cạnh của tam giác đó.
Trả lời
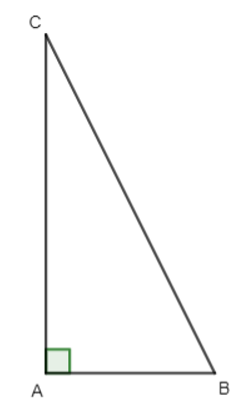
Gọi AB = x (cm) (x > 0)
Vì AB ngắn hơn AC là 2cm nên AC = x + 2 (cm).
a) Xét tam giác ABC vuông tại A, có:
BC2 = AB2 + AC2 (định lí Py – ta – go)
⇔ BC2 = x2 + (x + 2)2
⇔ BC2 = x2 + x2 + 4x + 4
⇔ BC2 = 2x2 + 4x + 4
⇔ BC = (cm)
Vậy BC = (cm).
b) Chu vi của tam giác ABC là:
AB + AC + BC = x + x + 2 + = 2x + 2 + (cm).
Mà chu vi của tam giác ABC là 24cm nên ta có phương trình:
2x + 2 + = 24
⇔ = 22 – 2x
⇒ 2x2 + 4x + 4 = 484 – 88x + 4x2
⇒ 2x2 – 92x + 480 = 0
⇒ x2 – 46x + 240 = 0
⇒ x = 40 và x = 6
Thay lần lượt hai nghiệm vào phương trình đã cho ta thấy x = 6 thỏa mãn.
Với x = 6 thì AB = 6 cm, AC = 6 + 2 = 8 cm, BC = cm.
Vậy độ dài các cạnh của tam giác ABC lần lượt là AB = 6cm, AC = 8cm, BC = 10 cm.
Xem thêm lời giải bài tập SGK Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 1: Dấu của tam thức bậc hai
Bài 2: Giải bất phương trình bậc hai một ẩn
Bài 3: Phương trình quy về phương trình bậc hai
Bài tập cuối chương 7
Bài 1: Quy tắc cộng và quy tắc nhân
Bài 2: Hoán vị, chỉnh hợp và tổ hợp

